13 Confluent Hypergeometric Functions Kummer Functions 13.6 Relations to Other Functions 13.8 Asymptotic Approximations for Large Parameters

§13.7 Asymptotic Expansions for Large Argument

ⓘ

Keywords:: Kummer functions, asymptotic expansions for large argument
Referenced by:: §13.29(i), §13.29(ii)
Permalink:: http://dlmf.nist.gov/13.7
See also:: Annotations for Ch.13

§13.7(i) Poincaré-Type Expansions

ⓘ

Notes:: See Temme (1996b, §7.2) or Olver (1997b, pp. 256–258).
Permalink:: http://dlmf.nist.gov/13.7.i
See also:: Annotations for §13.7 and Ch.13

As $x\to\infty$

13.7.1		${\mathbf{M}}\left(a,b,x\right)\sim\frac{e^{x}x^{a-b}}{\Gamma\left(a\right)}% \sum_{s=0}^{\infty}\frac{{\left(1-a\right)_{s}}{\left(b-a\right)_{s}}}{s!}x^{-% s},$
ⓘ Symbols: $\Gamma\left(\NVar{z}\right)$ : gamma function, ${\mathbf{M}}\left(\NVar{a},\NVar{b},\NVar{z}\right)$ : Olver’s confluent hypergeometric function, ${\left(\NVar{a}\right)_{\NVar{n}}}$ : Pochhammer’s symbol (or shifted factorial), $\sim$ : Poincaré asymptotic expansion, $\mathrm{e}$ : base of natural logarithm, $!$ : factorial (as in $n!$ ), $s$ : nonnegative integer and $x$ : real variable Permalink: http://dlmf.nist.gov/13.7.E1 Encodings: TeX, pMML, png See also: Annotations for §13.7(i), §13.7 and Ch.13

provided that $a\neq 0,-1,\dots$ .

As $z\to\infty$

13.7.2		${\mathbf{M}}\left(a,b,z\right)\sim\frac{e^{z}z^{a-b}}{\Gamma\left(a\right)}% \sum_{s=0}^{\infty}\frac{{\left(1-a\right)_{s}}{\left(b-a\right)_{s}}}{s!}z^{-% s}+\frac{e^{\pm\pi\mathrm{i}a}z^{-a}}{\Gamma\left(b-a\right)}\sum_{s=0}^{% \infty}\frac{{\left(a\right)_{s}}{\left(a-b+1\right)_{s}}}{s!}(-z)^{-s},$
$-\frac{1}{2}\pi+\delta\leq\pm\operatorname{ph}z\leq\frac{3}{2}\pi-\delta$ ,
ⓘ Symbols: $\Gamma\left(\NVar{z}\right)$ : gamma function, ${\mathbf{M}}\left(\NVar{a},\NVar{b},\NVar{z}\right)$ : Olver’s confluent hypergeometric function, ${\left(\NVar{a}\right)_{\NVar{n}}}$ : Pochhammer’s symbol (or shifted factorial), $\sim$ : Poincaré asymptotic expansion, $\pi$ : the ratio of the circumference of a circle to its diameter, $\mathrm{e}$ : base of natural logarithm, $!$ : factorial (as in $n!$ ), $\mathrm{i}$ : imaginary unit, $\operatorname{ph}$ : phase, $s$ : nonnegative integer, $z$ : complex variable and $\delta$ : small positive constant A&S Ref: 13.5.1 (with corrected region of validity) Referenced by: §13.2(iv), §13.7(ii), §13.9(i) Permalink: http://dlmf.nist.gov/13.7.E2 Encodings: TeX, pMML, png See also: Annotations for §13.7(i), §13.7 and Ch.13

unless $a=0,-1,\dots$ and $b-a=0,-1,\dots$ . Here $\delta$ denotes an arbitrary small positive constant. Also,

13.7.3		$U\left(a,b,z\right)\sim z^{-a}\sum_{s=0}^{\infty}\frac{{\left(a\right)_{s}}{% \left(a-b+1\right)_{s}}}{s!}(-z)^{-s},$
$\|\operatorname{ph}z\|\leq\tfrac{3}{2}\pi-\delta$ .
ⓘ Symbols: $U\left(\NVar{a},\NVar{b},\NVar{z}\right)$ : Kummer confluent hypergeometric function, ${\left(\NVar{a}\right)_{\NVar{n}}}$ : Pochhammer’s symbol (or shifted factorial), $\sim$ : Poincaré asymptotic expansion, $\pi$ : the ratio of the circumference of a circle to its diameter, $!$ : factorial (as in $n!$ ), $\operatorname{ph}$ : phase, $s$ : nonnegative integer, $z$ : complex variable and $\delta$ : small positive constant A&S Ref: 13.5.2 Referenced by: §12.9(i), §13.12, §13.2(i) Permalink: http://dlmf.nist.gov/13.7.E3 Encodings: TeX, pMML, png See also: Annotations for §13.7(i), §13.7 and Ch.13

§13.7(ii) Error Bounds

ⓘ

Keywords:: Kummer functions, asymptotic expansions for large argument, error bounds
Notes:: See Olver (1965).
Referenced by:: §12.9(ii), §13.19, Erratum (V1.0.19) for Notation
Permalink:: http://dlmf.nist.gov/13.7.ii
See also:: Annotations for §13.7 and Ch.13

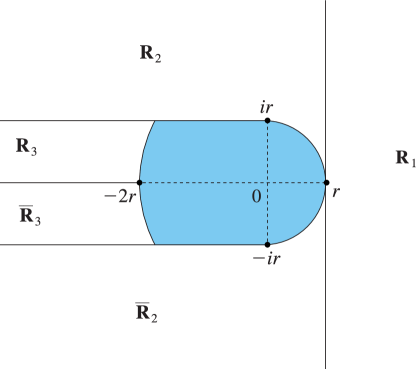
See accompanying text — Figure 13.7.1: Regions ${\textbf{R}}_{1}$ , ${\textbf{R}}_{2}$ , $\overline{\textbf{R}}_{2}$ , ${\textbf{R}}_{3}$ , and $\overline{\textbf{R}}_{3}$ are the closures of the indicated unshaded regions bounded by the straight lines and circular arcs centered at the origin, with $r=|b-2a|$ . Magnify

13.7.4		$U\left(a,b,z\right)=z^{-a}\sum_{s=0}^{n-1}\frac{{\left(a\right)_{s}}{\left(a-b% +1\right)_{s}}}{s!}(-z)^{-s}+\varepsilon_{n}(z),$
ⓘ Symbols: $U\left(\NVar{a},\NVar{b},\NVar{z}\right)$ : Kummer confluent hypergeometric function, ${\left(\NVar{a}\right)_{\NVar{n}}}$ : Pochhammer’s symbol (or shifted factorial), $!$ : factorial (as in $n!$ ), $n$ : nonnegative integer, $s$ : nonnegative integer, $z$ : complex variable and $\varepsilon_{n}(z)$ : function Referenced by: §13.2(i), §13.7(ii) Permalink: http://dlmf.nist.gov/13.7.E4 Encodings: TeX, pMML, png See also: Annotations for §13.7(ii), §13.7 and Ch.13

where

13.7.5		$\left\|\varepsilon_{n}(z)\right\|,~{}\beta^{-1}\left\|\varepsilon_{n}^{\prime}(z)% \right\|\leq 2\alpha C_{n}\left\|\frac{{\left(a\right)_{n}}{\left(a-b+1\right)_{% n}}}{n!z^{a+n}}\right\|\exp\left(\frac{2\alpha\rho C_{1}}{\|z\|}\right),$
ⓘ Defines: $\varepsilon_{n}(z)$ : function (locally) Symbols: ${\left(\NVar{a}\right)_{\NVar{n}}}$ : Pochhammer’s symbol (or shifted factorial), $\exp\NVar{z}$ : exponential function, $!$ : factorial (as in $n!$ ), $n$ : nonnegative integer, $z$ : complex variable, $C_{n}$ : coefficient, $\alpha$ , $\beta$ and $\rho$ Referenced by: §13.2(i) Permalink: http://dlmf.nist.gov/13.7.E5 Encodings: TeX, pMML, png See also: Annotations for §13.7(ii), §13.7 and Ch.13

and with the notation of Figure 13.7.1

13.7.6		$C_{n}=1,\quad\chi(n),\quad\left(\chi(n)+\sigma\nu^{2}n\right)\nu^{n},$
ⓘ Defines: $C_{n}$ : coefficient (locally) Symbols: $n$ : nonnegative integer, $\sigma$ , $\nu$ and $\chi(n)$ : function Permalink: http://dlmf.nist.gov/13.7.E6 Encodings: TeX, pMML, png See also: Annotations for §13.7(ii), §13.7 and Ch.13

according as

13.7.7		$z\in\textbf{R}_{1},\quad z\in\textbf{R}_{2}\cup\overline{\textbf{R}}_{2},\quad z% \in\textbf{R}_{3}\cup\overline{\textbf{R}}_{3},$
ⓘ Symbols: $\overline{\NVar{z}}$ : complex conjugate, $\in$ : element of, $\cup$ : union and $z$ : complex variable Permalink: http://dlmf.nist.gov/13.7.E7 Encodings: TeX, pMML, png See also: Annotations for §13.7(ii), §13.7 and Ch.13

respectively, with

13.7.8	$\displaystyle\sigma$	$\displaystyle=\left\|\ifrac{(b-2a)}{z}\right\|$ ,
	$\displaystyle\nu$	$\displaystyle=\left(\tfrac{1}{2}+\tfrac{1}{2}\sqrt{1-4\sigma^{2}}\right)^{-% \ifrac{1}{2}}$ ,
	$\displaystyle\chi(n)$	$\displaystyle=\sqrt{\pi}\Gamma\left(\tfrac{1}{2}n+1\right)/\Gamma\left(\tfrac{% 1}{2}n+\tfrac{1}{2}\right)$ .
ⓘ Defines: $\sigma$ (locally), $\nu$ (locally) and $\chi(n)$ : function (locally) Symbols: $\Gamma\left(\NVar{z}\right)$ : gamma function, $\pi$ : the ratio of the circumference of a circle to its diameter, $n$ : nonnegative integer and $z$ : complex variable Permalink: http://dlmf.nist.gov/13.7.E8 Encodings: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png See also: Annotations for §13.7(ii), §13.7 and Ch.13

Also, when $z\in\textbf{R}_{1}\cup\textbf{R}_{2}\cup\overline{\textbf{R}}_{2}$

13.7.9	$\displaystyle\alpha$	$\displaystyle=\frac{1}{1-\sigma}$ ,
	$\displaystyle\beta$	$\displaystyle=\frac{1-\sigma^{2}+\sigma\|z\|^{-1}}{2(1-\sigma)}$ ,
	$\displaystyle\rho$	$\displaystyle=\tfrac{1}{2}\left\|2a^{2}-2ab+b\right\|+\frac{\sigma(1+\frac{1}{4}% \sigma)}{(1-\sigma)^{2}}$ ,
ⓘ Defines: $\alpha$ (locally), $\beta$ (locally) and $\rho$ (locally) Symbols: $z$ : complex variable and $\sigma$ Referenced by: §13.7(ii), §13.7(ii) Permalink: http://dlmf.nist.gov/13.7.E9 Encodings: TeX, TeX, TeX, pMML, pMML, pMML, png, png, png See also: Annotations for §13.7(ii), §13.7 and Ch.13

and when $z\in\textbf{R}_{3}\cup\overline{\textbf{R}}_{3}$ $\sigma$ is replaced by $\nu\sigma$ and $|z|^{-1}$ is replaced by $\nu|z|^{-1}$ everywhere in (13.7.9).

For numerical values of $\chi(n)$ see Table 9.7.1.

Corresponding error bounds for (13.7.2) can be constructed by combining (13.2.41) with (13.7.4)–(13.7.9).

§13.7(iii) Exponentially-Improved Expansion

ⓘ

Keywords:: Kummer functions, asymptotic expansions for large argument, exponentially-improved, hyperasymptotic
Referenced by:: §12.9(ii), §13.19, Erratum (V1.0.10) for References
Permalink:: http://dlmf.nist.gov/13.7.iii
Addition (effective with 1.0.10):: A sentence and reference to Paris (2013) were added at the end of this subsection.
See also:: Annotations for §13.7 and Ch.13

Let

13.7.10		$U\left(a,b,z\right)=z^{-a}\sum_{s=0}^{n-1}\frac{{\left(a\right)_{s}}{\left(a-b% +1\right)_{s}}}{s!}(-z)^{-s}+R_{n}(a,b,z),$
ⓘ Symbols: $U\left(\NVar{a},\NVar{b},\NVar{z}\right)$ : Kummer confluent hypergeometric function, ${\left(\NVar{a}\right)_{\NVar{n}}}$ : Pochhammer’s symbol (or shifted factorial), $!$ : factorial (as in $n!$ ), $n$ : nonnegative integer, $s$ : nonnegative integer, $z$ : complex variable and $R_{n}(a,b,z)$ : remainder Referenced by: §13.29(i) Permalink: http://dlmf.nist.gov/13.7.E10 Encodings: TeX, pMML, png See also: Annotations for §13.7(iii), §13.7 and Ch.13

and

13.7.11		$R_{n}(a,b,z)=\frac{(-1)^{n}2\pi z^{a-b}}{\Gamma\left(a\right)\Gamma\left(a-b+1% \right)}\left(\sum_{s=0}^{m-1}\frac{{\left(1-a\right)_{s}}{\left(b-a\right)_{s% }}}{s!}(-z)^{-s}G_{n+2a-b-s}(z)+{\left(1-a\right)_{m}}{\left(b-a\right)_{m}}R_% {m,n}(a,b,z)\right),$
ⓘ Defines: $R_{n}(a,b,z)$ : remainder (locally) Symbols: $\Gamma\left(\NVar{z}\right)$ : gamma function, ${\left(\NVar{a}\right)_{\NVar{n}}}$ : Pochhammer’s symbol (or shifted factorial), $\pi$ : the ratio of the circumference of a circle to its diameter, $!$ : factorial (as in $n!$ ), $m$ : integer, $n$ : nonnegative integer, $s$ : nonnegative integer, $z$ : complex variable and $G_{p}(z)$ : expansion Referenced by: §13.29(i) Permalink: http://dlmf.nist.gov/13.7.E11 Encodings: TeX, pMML, png See also: Annotations for §13.7(iii), §13.7 and Ch.13

where $m$ is an arbitrary nonnegative integer, and

13.7.12		$G_{p}(z)=\frac{e^{z}}{2\pi}\Gamma\left(p\right)\Gamma\left(1-p,z\right).$
ⓘ Defines: $G_{p}(z)$ : expansion (locally) Symbols: $\Gamma\left(\NVar{z}\right)$ : gamma function, $\pi$ : the ratio of the circumference of a circle to its diameter, $\mathrm{e}$ : base of natural logarithm, $\Gamma\left(\NVar{a},\NVar{z}\right)$ : incomplete gamma function and $z$ : complex variable Permalink: http://dlmf.nist.gov/13.7.E12 Encodings: TeX, pMML, png See also: Annotations for §13.7(iii), §13.7 and Ch.13

(For the notation see §8.2(i).) Then as $z\to\infty$ with $\left|\left|z\right|-n\right|$ bounded and $a, b, m$ fixed

13.7.13		$R_{m,n}(a,b,z)=\begin{cases}O\left(e^{-\|z\|}z^{-m}\right),&\|\operatorname{ph}z\|% \leq\pi,\\ O\left(e^{z}z^{-m}\right),&\pi\leq\|\operatorname{ph}z\|\leq\tfrac{5}{2}\pi-% \delta.\\ \end{cases}$
ⓘ Symbols: $O\left(\NVar{x}\right)$ : order not exceeding, $\pi$ : the ratio of the circumference of a circle to its diameter, $\mathrm{e}$ : base of natural logarithm, $\operatorname{ph}$ : phase, $m$ : integer, $n$ : nonnegative integer, $z$ : complex variable, $\delta$ : small positive constant and $R_{n}(a,b,z)$ : remainder Permalink: http://dlmf.nist.gov/13.7.E13 Encodings: TeX, pMML, png See also: Annotations for §13.7(iii), §13.7 and Ch.13

For proofs see Olver (1991b, 1993a). For the special case $\operatorname{ph}z=\pm\pi$ see Paris (2013). For extensions to hyperasymptotic expansions see Olde Daalhuis and Olver (1995a).

13.6 Relations to Other Functions 13.8 Asymptotic Approximations for Large Parameters

Site Privacy Accessibility Privacy Program Copyrights Vulnerability Disclosure No Fear Act Policy FOIA Environmental Policy Scientific Integrity Information Quality Standards Commerce.gov Science.gov USA.gov

Note: This service is not intended for secure transactions such as banking, social media, email, or purchasing. Use at your own risk. We assume no liability whatsoever for broken pages.

§13.7 Asymptotic Expansions for Large Argument

Contents

§13.7(i) Poincaré-Type Expansions

§13.7(ii) Error Bounds

§13.7(iii) Exponentially-Improved Expansion

Pfad - The Proxy pFad of © 2024 Garber Painting. All rights reserved.