19 Elliptic Integrals Symmetric Integrals 19.16 Definitions 19.18 Derivatives and Differential Equations

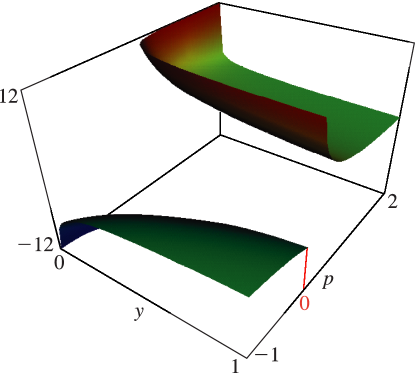
§19.17 Graphics

ⓘ

Keywords:: graphics, symmetric elliptic integrals
Notes:: These graphics were produced at NIST.
Permalink:: http://dlmf.nist.gov/19.17
See also:: Annotations for Ch.19

See Figures 19.17.1–19.17.8 for symmetric elliptic integrals with real arguments.

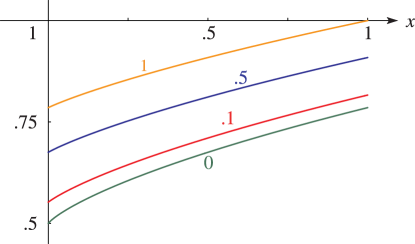
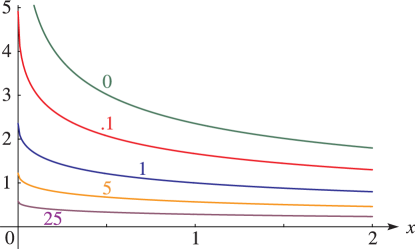
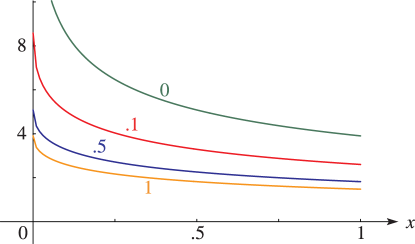
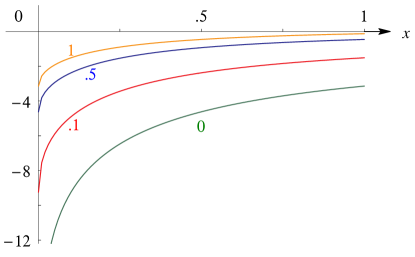
Because the $R$ -function is homogeneous, there is no loss of generality in giving one variable the value $1$ or $-1$ (as in Figure 19.3.2). For $R_{F}$ , $R_{G}$ , and $R_{J}$ , which are symmetric in $x, y, z$ , we may further assume that $z$ is the largest of $x, y, z$ if the variables are real, then choose $z=1$ , and consider only $0\leq x\leq 1$ and $0\leq y\leq 1$ . The cases $x=0$ or $y=0$ correspond to the complete integrals. The case $y=1$ corresponds to elementary functions.

To view $R_{F}\left(0,y,1\right)$ and $2R_{G}\left(0,y,1\right)$ for complex $y$ , put $y=1-k^{2}$ , use (19.25.1), and see Figures 19.3.7–19.3.12.

See accompanying text — Figure 19.17.1: $R_{F}\left(x,y,1\right)$ for $0\leq x\leq 1$ , $y=0,\,0.1,\,0.5,\,1$ . $y=1$ corresponds to $R_{C}\left(x,1\right)$ . Magnify

To view $R_{F}\left(0,y,1\right)$ and $2R_{G}\left(0,y,1\right)$ for complex $y$ , put $y=1-k^{2}$ , use (19.25.1), and see Figures 19.3.7–19.3.12.

19.16 Definitions 19.18 Derivatives and Differential Equations

Site Privacy Accessibility Privacy Program Copyrights Vulnerability Disclosure No Fear Act Policy FOIA Environmental Policy Scientific Integrity Information Quality Standards Commerce.gov Science.gov USA.gov

Note: This service is not intended for secure transactions such as banking, social media, email, or purchasing. Use at your own risk. We assume no liability whatsoever for broken pages.

§19.17 Graphics

Pfad - The Proxy pFad of © 2024 Garber Painting. All rights reserved.