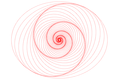
DescriptionOsculating circles of the Archimedean spiral.svg	English: Osculating circles of the Archimedean spiral. "The spiral itself is not not drawn: we see it as the locus of points where the circles are especially close to each other." [1]
Date	27 May 2019
Source	Own work
Author	Adam majewski
Other versions	Nested Ellipses.png Osculating circle.svg Log spiral with osculating circles.jpg
SVG development InfoField	The SVG code is valid.   This plot was created with Gnuplot.    This plot uses embedded text that can be easily translated using a text editor.

Point ${\displaystyle z_{t}}$ of an Archimedean spiral for angle t

  ${\displaystyle x_{t}=f(t)=t*cos(t)}$

  ${\displaystyle y_{t}=g(t)=t*sin(t)}$

 ${\displaystyle z_{t}=x_{t}+y_{t}*i}$

The curvature of Archimedes' spiral is

${\displaystyle K(t)={\frac {2+t^{2}}{(1+t^{2})^{3/2}}}}$

Radius of osculating circle is^[2]

${\displaystyle R(t)={\frac {1}{|K(t)|}}}$

Center of osculating circle is

 ${\displaystyle z_{c,t}=x_{c,t}+y_{c,t}*i}$

 ${\displaystyle x_{c,t}=f-{\frac {(f'^{2}+g'^{2})g'}{f'^{2}g''-f''g'}}}$

 ${\displaystyle y_{c,t}=g+{\frac {(f'^{2}+g'^{2})f'}{f'^{2}g''-f''g'}}}$

where

• ${\displaystyle f=f(t)}$
• ${\displaystyle f'={\frac {df}{dt}}(t)}$ is first derivative
• ${\displaystyle f'^{2}=f'*f'}$
• ${\displaystyle f''}$ is a second derivative

Program computes 130 values of angle ( list tt) from 1/5 to 26:

 [1/5,2/5,3/5,4/5,1,6/5,7/5,8/5,9/5,2,11/5,12/5,13/5,14/5,3,16/5,17/5,18/5,19/5,4,21/5,22/5,23/5,24/5,5,26/5,27/5,28/5,29/5,6,31/5,32/5,
        33/5,34/5,7,36/5,37/5,38/5,39/5,8,41/5,42/5,43/5,44/5,9,46/5,47/5,48/5,49/5,10,51/5,52/5,53/5,54/5,11,56/5,57/5,58/5,59/5,12,61/5,62/5,
        63/5,64/5,13,66/5,67/5,68/5,69/5,14,71/5,72/5,73/5,74/5,15,76/5,77/5,78/5,79/5,16,81/5,82/5,83/5,84/5,17,86/5,87/5,88/5,89/5,18,91/5,92/5,
        93/5,94/5,19,96/5,97/5,98/5,99/5,20,101/5,102/5,103/5,104/5,21,106/5,107/5,108/5,109/5,22,111/5,112/5,113/5,114/5,23,116/5,117/5,118/5,
        119/5,24,121/5,122/5,123/5,124/5,25,126/5,127/5,128/5,129/5,26]

For each angle t computes circle ( list for draw2d). It gives a new list Circles

 Circles : map (GiveCircle, tt)$ 

Command draw2d takes list Circles and draw all circles. Commands from draw package accepts list as an input.

• compute a list of angles
• For each angle t from list tt compute a point ${\displaystyle z_{t}}$
• for each point ${\displaystyle z_{t}}$ compute and draw osculating circle

/*


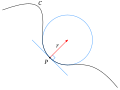
http://mathworld.wolfram.com/OsculatingCircle.html
The osculating circle of a curve C at a given point  P 
is the circle that has the same tangent as C at point P as well as the same curvature. 



https://en.wikipedia.org/wiki/Archimedean_spiral
https://www.mathcurve.com/courbes2d.gb/archimede/archimede.shtml

https://www.mathcurve.com/courbes2d.gb/enveloppe/enveloppe.shtml

the osculating circles of an Archimedean spiral. There is no need to trace the envelope...

http://xahlee.info/SpecialPlaneCurves_dir/ArchimedeanSpiral_dir/archimedeanSpiral.html

The tangent circles of Archimedes's spiral are all nested. need to proof that archimedes spiral's osculating circles are nested inside each other.

https://arxiv.org/abs/math/0602317
https://www.researchgate.net/publication/236899971_Osculating_Curves_Around_the_Tait-Kneser_Theorem



Osculating Curves: Around the Tait-Kneser Theorem
March 2013The Mathematical Intelligencer 35(1):61-66
DOI: 10.1007/s00283-012-9336-6
Elody GhysElody GhysSerge TabachnikovSerge TabachnikovVladlen TimorinVladlen Timorin

Osculating circles of a spiral. The spiral itself is not not drawn:
we see it as the locus of points where the circles are especially close to each
other.




https://math.stackexchange.com/questions/568752/curvature-of-the-archimedean-spiral-in-polar-coordinates

===============
Batch file for Maxima CAS
save as a a.mac
run maxima : 
 maxima
and then : 
batch("a.mac");




*/


kill(all);
remvalue(all);
ratprint:false;


/* ---------- functions ---------------------------------------------------- */




/* 
converts complex number z = x*y*%i 
to the list in a draw format:  
[x,y] 
*/
draw_f(z):=[float(realpart(z)), float(imagpart(z))]$

/* give Draw List from one point*/
dl(z):=points([draw_f(z)])$

ToPoints(myList):= points(map(draw_f , myList))$








f(t):= t*cos(t)$
g(t) :=t*sin(t)$


define(fp(t), diff(f(t),t,1));
define(fpp(t),	diff(f(t),t,2));
define(gp(t), diff(g(t),t,1));
define(gpp(t), diff(g(t),t,2));


/* 
 point of the Archimedean spiral
 
 
 
 t is angle in turns 
 1 turn = 360 degree = 2*Pi radians 
 
 
*/
give_spiral_point(t):= f(t)+ %i*g(t)$


/* The curvature of Archimedes' spiral is
http://mathworld.wolfram.com/ArchimedesSpiral.html

 */
GiveCurvature(t) := (2+t*t)/sqrt((1+t*t)*(1+t*t)*(1+t*t)) $


GiveRadius(t):= float(1/GiveCurvature(t));
/*
center of The osculating circle of a curve C at a given point  P = give_spiral_point(t)
*/
GiveCenter(T):= block(
	[x, y,f_, f_p, f_pp, g_, g_p, g_pp, n, d ],
	f_ : f(T),
	f_p : fp(T),
	f_pp : fpp(T),
	g_ : g(T),
	g_p : gp(T),
	g_pp : gpp(T),
	n : f_p*f_p + g_p*g_p, 
	d : f_p*g_pp - f_pp*g_p,
	x: f_ - g_p*n/d,
	y: g_ + f_p* n/d,
	return ( x+y*%i)
	
)$


GiveCircle(T):= block(
	[Center, Radius],
	Center : GiveCenter(T),
	Radius : GiveRadius(T),
	return(ellipse (float(realpart(Center)), float(imagpart(Center)), Radius, Radius, 0, 360))

)$ 





/* compute */

iMin:1;
iMax:130;
id:5;

tt: makelist(i/id, i, iMin, iMax)$

zz: map(give_spiral_point, tt)$ /* points of the spiral */

Circles : map (GiveCircle, tt)$

/* convert lists  to draw format */
points: ToPoints(zz )$



/* draw lists using draw package */

path:"~/maxima/batch/spiral/ARCHIMEDEAN_SPIRAL/a2/"$ /*  pwd, if empty then file is in a home dir , path should end with "/" */

/* draw it using draw package by */

 load(draw); 
/* if graphic  file is empty (= 0 bytes) then run draw2d command again */

 draw2d(
  user_preamble="set key top right; unset mouse",
  terminal  = 'svg,
  file_name = sconcat(path,"spiral_rc13_", string(iMin),"_", string(iMax)),
  font_size = 13,
  font = "Liberation Sans", /* https://commons.wikimedia.org/wiki/Help:SVG#Font_substitution_and_fallback_fonts */
  title= "Osculating circles of the Archimedean spiral.\ The spiral itself is not not drawn: we see it as the locus of points where the circles are especially close to each other.",
    
  dimensions = [1000, 1000],
  /* points  of the spiral, if you want to check 
  point_type    = filled_circle,
  point_size    = 1,
  points_joined = true,
  points,*/
  /* circles */
  key = "",
  line_width = 1,
  line_type = solid,
  border = true, 
  nticks = 100, 
  color = red,
  fill_color = white,
  transparent = true,
  Circles
  
  
  
  )$
  

I, the copyright holder of this work, hereby publish it under the following license:

This file is licensed under the Creative Commons Attribution-Share Alike 4.0 International license.

You are free:

• to share – to copy, distribute and transmit the work
• to remix – to adapt the work

Under the following conditions:

• attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
• share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.

https://creativecommons.org/licenses/by-sa/4.0CC BY-SA 4.0 Creative Commons Attribution-Share Alike 4.0 truetrue

• benice-equation : nested-ellipses

1. ↑ Osculating curves: around the Tait-Kneser Theoremby E. Ghys, S. Tabachnikov, V. Timorin
2. ↑ mathworld.wolfram : OsculatingCircle