|
| 1 | +<!--?title 15 Puzzle Game: Existence Of The Solution --> |
| 2 | + |
| 3 | +# 15 Puzzle Game: Existence Of The Solution |
| 4 | + |
| 5 | +This game is played on board, which size is 4×4 cells. On this board there are 15 playing tiles numbered from 1 to 15. One cell is left empty. It is required to come to position presented below by moving some tiles to the free space: |
| 6 | + |
| 7 | + |
| 8 | + |
| 9 | +The game "15 Puzzle” was created by Noyes Chapman in 1880. |
| 10 | + |
| 11 | + |
| 12 | + |
| 13 | +## Existence Of The Solution |
| 14 | + |
| 15 | + |
| 16 | + |
| 17 | +Let's consider this problem: given position on the board to determine whether exists such a sequence of moves, which leads to a solution. |
| 18 | + |
| 19 | +Suppose, we have some position on the board: |
| 20 | + |
| 21 | + |
| 22 | + |
| 23 | +where one of the elements equals zero and indicates an empty cell $a_z = 0$ |
| 24 | + |
| 25 | +Let’s consider the permutation: |
| 26 | + |
| 27 | +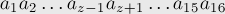 |
| 28 | + |
| 29 | +(i.e. the permutation of numbers corresponding to the position on the board, without a zeroth element) |
| 30 | + |
| 31 | +Let $N$ be a quantity of inversions in this permutation (i.e. the quantity of such elements $a_i$ and $a_j$ that $i < j$, but $a_i > a_j$). |
| 32 | + |
| 33 | +Suppose $K$ is an index of a row where the empty element is located (i.e. in our indications $K = (z - 1) \ div \ 4 + 1$). |
| 34 | + |
| 35 | +Then, **the solution exists iff $N + K$ is even**. |
| 36 | + |
| 37 | + |
| 38 | + |
| 39 | +## Implementation |
| 40 | + |
| 41 | + |
| 42 | + |
| 43 | +The algorithm above can be illustrated with the following program code: |
| 44 | + |
| 45 | +````cpp |
| 46 | +int a[16]; |
| 47 | +for (int i=0; i<16; ++i) |
| 48 | + cin >> a[i]; |
| 49 | + |
| 50 | +int inv = 0; |
| 51 | +for (int i=0; i<16; ++i) |
| 52 | + if (a[i]) |
| 53 | + for (int j=0; j<i; ++j) |
| 54 | + if (a[j] > a[i]) |
| 55 | + ++inv; |
| 56 | +for (int i=0; i<16; ++i) |
| 57 | + if (a[i] == 0) |
| 58 | + inv += 1 + i / 4; |
| 59 | + |
| 60 | +puts ((inv & 1) ? "No Solution" : "Solution Exists"); |
| 61 | +```` |
| 62 | +
|
| 63 | +
|
| 64 | +## Proof |
| 65 | +
|
| 66 | +
|
| 67 | +In 1879 Johnson proved that if $N + K$ is odd, then the solution doesn’t exist, and in the same year Story proved that all positions when $N + K$ is even have a solution. |
| 68 | +
|
| 69 | +However, all these proofs were quite complex. |
| 70 | +
|
| 71 | +In 1999 Archer proposed much more simple proof (you can download his article [here](http://www.cs.cmu.edu/afs/cs/academic/class/15859-f01/www/notes/15-puzzle.pdf)). |
0 commit comments