Abstract
Linkage studies of complex traits frequently yield multiple linkage regions covering hundreds of genes. Testing each candidate gene from every region is prohibitively expensive and computational methods that simplify this process would benefit genetic research. We present a new method based on commonality of functional annotation (CFA) that aids dissection of complex traits for which multiple causal genes act in a single pathway or process. CFA works by testing individual Gene Ontology (GO) terms for enrichment among candidate gene pools, performs multiple hypothesis testing adjustment using an estimate of independent tests based on correlation of GO terms, and then scores and ranks genes annotated with significantly-enriched terms based on the number of quantitative trait loci regions in which genes bearing those annotations appear. We evaluate CFA using simulated linkage data and show that CFA has good power despite being conservative. We apply CFA to published linkage studies investigating age-of-onset of Alzheimer's disease and body mass index and obtain previously known and new candidate genes. CFA provides a new tool for studies in which causal genes are expected to participate in a common pathway or process and can easily be extended to utilize annotation schemes in addition to the GO.
INTRODUCTION
Analysis of Mendelian traits is characterized by phenotypes being highly informative about the underlying genotypes (1). In contrast, analysis of complex traits is characterized by phenotypes being uninformative about the underlying genotypes (1). Complex traits are typically weakly correlated to many genes or chromosomal regions distributed across the genome. If a trait is quantitatively measured, regions of the genome containing genetic variation that influences the quantitative trait being considered are called quantitative trait loci (QTL). One limitation of linkage analysis is that its resolution is generally low, such that potentially hundreds of genes may be contained within a single QTL. Narrowing the list of positional candidate genes via comprehensive wet-lab experimentation is often prohibitively laborious and expensive.
If multiple genes correlate to the same trait, then it is reasonable to hypothesize that those genes are more likely to share one or more annotations compared with genes not correlated to that trait (2). If the hypothesis is correct, then one way to narrow a list of candidate genes resulting from a genome-wide linkage study is to search for annotations that are enriched among the candidate genes relative to randomly sampled genes and then prioritize candidate genes on the basis of those annotations. The benefit is a reduced amount of wet-lab experimentation required to identify causal genes. In the past few years, several groups have published bioinformatic methods for narrowing lists of candidate genes using a variety of gene annotations, such as gene length, expression profiles and patterns of gene duplication (3). If the hypothesis is incorrect, so long as the prioritization procedure does not result in the removal of any genes from the list or introduce misinformation, then there is minimal cost.
In this study, we used a statistical bioinformatic approach based on Gene Ontology (GO) annotation (4) to prioritize candidate genes from multiple QTL. The GO is a controlled vocabulary of terms that are organized in parent-child relationships, in which each term may have one or more parent terms. All terms ultimately descend from one of three roots: molecular function, cellular component, or biological process. These roots and their descendent child terms represent three different ways of categorizing knowledge about genes and gene products: (i) their known or predicted molecular function (e.g. type of biochemical activity), (ii) cellular locale (e.g. nucleus), or (iii) their biological role (e.g. transcription, learning and memory). A given gene, depending on the level of knowledge about it, can be annotated with terms from any of these three parts of the GO, which are also sometimes called sub-ontologies.
The GO has been used extensively in recent years as a way to mine large data sets obtained from genome-scale experiments. The typical approach has been to determine which GO terms are enriched among a given group of ‘interesting genes’, such as a list of differentially expressed genes obtained from an expression microarray experiment [see the review (5)]. Enriched GO terms serve as a description of molecular functions, cellular components, or biological processes that are most relevant to the trait under investigation.
Enrichment of GO terms for a list of genes is commonly evaluated using Fisher's exact test (5,6), which is based on the hypergeometric distribution for sampling without replacement (7). One limitation of this approach, however, is that terms are tested one at a time, ignoring the relationships between terms. As a result, subsequent corrections for multiple hypothesis testing tend to be too extreme, since tests of highly correlated terms (e.g. parents and their children) are incorrectly treated as independent. Another issue is that although the three sub-ontologies are structurally disjoint, terms both within and between sub-ontologies may be further correlated due to the fact that genes may be annotated by many terms from any of the three sub-ontologies simultaneously. To account for both sources of correlation, we developed a method that achieves dimension reduction, through principal components analysis, of the correlation structure across all GO terms in conjunction with testing for enrichment of GO terms. We then applied this method to the task of candidate gene identification and implemented a novel scoring scheme for prioritizing all candidate genes under each of any arbitrary number of QTL. We named this method Commonality of Functional Annotation (CFA). We assessed the false positive error rate and power of CFA through simulation. Finally, we applied CFA to real data sets for two quantitative, complex human traits: (i) for age-of-onset of Alzheimer's disease and (ii) for body mass index (BMI).
MATERIALS AND METHODS
Materials
For the data set for Alzheimer's disease, we considered a set of three QTL shown in Table 1. The quantitative trait was age-of-onset and none of the three QTL was specific for early- versus late-onset disease (8). For the data set for BMI, we performed a PubMed search to identify genome-wide linkage scans in humans. BMI is an anthropometric measure defined as weight in kilograms divided by the square of height in meters. BMI is thus a continuous measure and can be used as a quantitative trait. A BMI from 25 to 30 kg/m2 refers to overweight and a BMI in excess of 30 kg/m2 refers to obese (http://win.niddk.nih.gov/publications/glossary/AthruL.htm). The compiled list of 18 QTL for BMI (9–18) is displayed in Table 2.
Table 1.
QTL analyzed for Alzheimer's disease
Table 2.
QTL analyzed for body mass index
| Chromosome | Nucleotide start | Nucleotide end | Reference |
|---|---|---|---|
| 1p36 | 1 | 13368006 | (18) |
| 1p22 | 81686191 | 101686191 | (17) |
| 2q14 | 114345119 | 134345119 | (18) |
| 3q22 | 138413583 | 158413583 | (17) |
| 3q27 | 167105819 | 187105819 | (16) |
| 4q12 | 47597526 | 67597526 | (18) |
| 5q12 | 56263229 | 76263229 | (14) |
| 5q32 | 135232609 | 155232609 | (14) |
| 6p25 | 765305 | 12968512 | (15) |
| 6q23-25 | 137282655 | 162104889 | (12) |
| 7p21 | 18028844 | 27780107 | (15) |
| 7q32 | 121695999 | 141695999 | (13) |
| 10p11 | 18725142 | 31684305 | (14) |
| 11q14 | 117235383 | 128161860 | (12) |
| 13q14 | 42330695 | 62330695 | (13) |
| 16p11-12 | 23004204 | 26125659 | (11) |
| 19q13 | 50237821 | 70237821 | (10) |
| 20q13 | 28737193 | 48737193 | (9) |
Methods
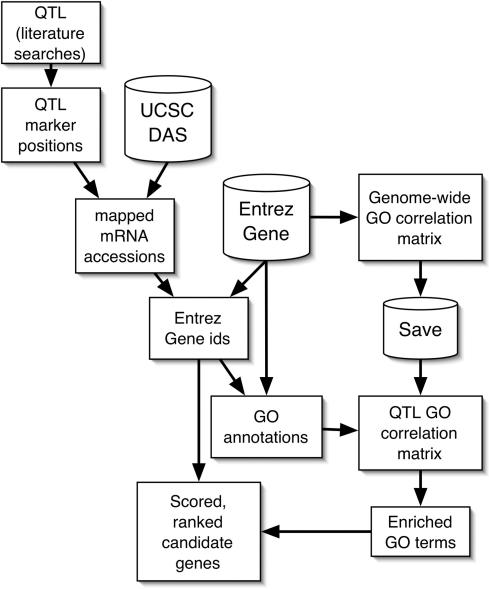
Figure 1 depicts the flow of data through the CFA procedure. A collection of Python scripts, R code, data files and documentation is freely available at http://www.transvar.org/candi_gene. The details of each step are described below.
Figure 1.
Workflow diagram. The flow of data from each step is schematically depicted. The genome-wide correlation matrix is computed for all GO terms and saved for subsequent analysis with different data sets. Genes overlapping with QTL regions and their associated GO annotations are obtained from the UCSC Genome Informatics DAS/1 server and the Entrez Gene database, respectively. For each data set, a study-specific correlation matrix is blocked from the genome-wide correlation matrix. Genes from each QTL are combined to form a study-wide gene list and each term is then tested for over-representation using Fisher's exact test. The effective number of independent tests is estimated using Velicer's minimum average partial test, and P-values obtained are adjusted upward based on the effective number of independent tests. Genes are then scored using weights computed from principal components of the study-specific correlation matrix and the number of QTL containing genes with enriched annotations. Rectangles indicate products of data processing and cylinders indicate databases.
Collecting genes and GO annotations
We obtained the genomic coordinates for each marker from the primary reference or from the International HapMap Project (http://www.hapmap.org). If provided in the primary reference, we used the stated confidence intervals to determine genomic coordinates for QTL. If a confidence interval was not provided, we assumed that the interval spanned ±10 Mb centered on the marker. Assuming that 1 Mb corresponds to 1 cM, this width corresponds to a confidence interval of ±10 cM (19). This parameter is user-definable for use with any data set. We then used the UCSC Genome Informatics DAS/1 server (http://genome.ucsc.edu) [NCBI B35 assembly (20)] to retrieve GenBank accessions for mRNAs mapping to each QTL. A list of unique Entrez Gene ids corresponding to the retrieved mRNA accessions (a many-to-one mapping) was generated using the 9 May 2006 release of the gene2accession file available from the NCBI Entrez Gene ftp site (ftp://ftp.ncbi.nlm.nih.gov/gene). All GO annotations for unique Entrez Gene ids (a one-to-many mapping) were retrieved from the 9 May 2006 release of the gene2go file, also available from the NCBI Entrez Gene ftp site (ftp://ftp.ncbi.nlm.nih.gov/gene).
Constructing a genome-wide GO term correlation matrix
The gene2go file release used in this study included 5147 GO terms annotating 16 114 Homo sapiens genes. For each term, we recorded the number of unique Entrez Gene ids annotated with that term. Let fi represent the count of genes annotated by the i-th term and let pi = fi / n with n = 16 114 genes. Then, for each pair of GO terms, we recorded the number of genes annotated with both of those terms. Let fij represent the count of genes annotated by both the i-th and j-th terms, for i ≠ j. We built a genome-wide correlation matrix R of dimensions n × n from these counts using the Pearson correlation coefficient for binomially distributed data, also known as the phi coefficient (http://www.visualstatistics.net/Visual%20Statistics%20Multimedia/crosstabulation.htm), defined as
To illustrate, consider GO:0005634 and GO:0003700, which represent the cellular component ‘nucleus’ and molecular function ‘transcription factor activity’, respectively. The number of unique Entrez Gene ids annotated with ‘nucleus’ is f1 = 3701, the number of unique Entrez Gene ids annotated with ‘transcription factor activity’ is f2 = 890 and the number of unique Entrez Gene ids annotated with both ‘nucleus’ and ‘transcription factor activity’ is f12 = 868. Using n = 16 114, the phi coefficient between ‘nucleus’ and ‘transcription factor activity’ is rij = 0.429.
Additionally, conditional probabilities can be used to demonstrate that there is a relationship between terms that belong to disjoint sub-ontologies. For example, the conditional probability of a gene being annotated with ‘nucleus’, given that the gene is annotated with ‘transcription factor activity’, is pr(p1/p2)=0.975. Similarly, the conditional probability of a gene being annotated with ‘transcription factor activity’, given that the gene is annotated with ‘nucleus’, is pr(p1/p2)=0.234. Thus, there is strong correlation between these two terms even though they belong to disjoint sub-ontologies.
Testing for GO term enrichment
Consider the union of all K genes and L terms over all QTL linked to a trait. Table 3 shows the set-up for testing GO terms for enrichment. Let A represent the observed count of genes in the list annotated by a GO term. Let A + B represent the total count of genes annotated by a GO term among all genes. Let K = A + C represent the total number of genes in the list. Let A + B + C + D represent the total number of genes, which is also given by n = 16 114. Enrichment for the GO term was determined using a one-tailed Fisher's exact test.
Table 3.
2 × 2 Table for Fisher's exact test for enrichment of a Gene Ontology term
| Gene in list | Gene not in list | Total | |
|---|---|---|---|
| Gene annotated with term | A | B | A + B |
| Gene not annotated with term | C | D | C + D |
| Total | A + C | B + D | A + B + C + D |
Adjusting for multiple, correlated tests
A popular method for controlling the false positive error rate among m independent tests is the full Bonferroni correction, which involves decreasing the per comparison significance level from α to α/m. If the tests are correlated, then a partial Bonferroni correction is more appropriate, with the correction being some value smaller than m. Since tests of GO term enrichment are correlated, a partial Bonferroni correction is more appropriate than a full Bonferroni correction.
To determine an appropriate correction factor for multiple tests in the presence of correlation, we first partitioned the genome-wide correlation matrix as
in which R1 is an L × L block corresponding to the L observed GO terms relevant to the data set being analyzed. Then, we performed Velicer's minimum average partial (MAP) test on R1 to estimate the number of principal components that should be retained (21,22). Briefly, Velicer's MAP test involves partialling out principal components from the correlation matrix and computing the average squared partial correlation (22). The number of retained principal components minimizes the average squared partial correlation (22). Since each principal component is associated with one eigenvector, and eigenvectors are orthogonal, we equated the number of retained principal components to the effective number of independent tests and all P-values were multiplied by this value. If all principal components were retained, then the partial and full Bonferroni corrections were identical. If only some principal components were retained, then the partial Bonferroni correction was smaller than the full Bonferroni correction, allowing for more rejections and retaining more power. The criterion for declaring a test for enrichment significant was that the adjusted P-value be <0.05.
Scoring genes
Let M represent a binary incidence matrix of k=1,2, …, K rows (genes) and l = 1,2,…,L columns (GO terms). Values in the incidence matrix are
 |
Let P represent the L × L matrix of orthonormalized eigenvectors calculated from the L × L correlation matrix R1. Eigenvectors are used to model the correlation among GO terms so that redundant information represented by correlated GO terms is not double-counted in the score for a given gene. Let w represent a L × 1 vector of weights, in which weights were assigned to each term by counting the number of QTL in which that term annotated at least one gene. A K × 1 vector of weighted scores was calculated as s=MPw. For the list of genes under a QTL, scores were ranked and the top ranked gene (or genes, in the case of ties) was considered to be the prioritized candidate gene for that QTL. This weighting scheme yields higher scores for enriched GO terms associated with multiple QTL. This scheme is based on the assumption that the recurrence of a significantly enriched GO term, with respect to multiple QTL, increases our belief that concluding significant enrichment for that particular GO term reflects a true positive result.
Assessment of the false positive error rate
To assess the false positive error rate for GO term enrichment, we simulated data under the null hypothesis that a GO term annotates genes contained in the QTL as often as it annotates genes not in the QTL. To randomly generate a QTL, we randomly sampled a genomic position, using probabilities proportional to chromosome length, and defined the QTL as the interval covering 20 Mb centered on that position. The false positive error rate was defined as the percent of GO terms that were determined to be significantly enriched. We simulated data sets of two sizes, one containing three non-overlapping QTL and one containing six non-overlapping QTL. For both sizes, we generated 100 independent replicates (i.e. data sets).
Assessment of power
To assess power, we simulated data under the alternative hypothesis. Under the alternative hypothesis, a GO term annotates genes in the QTL more often that it annotates genes not in the QTL. To simulate data under this alternative hypothesis, we randomly sampled a GO term that annotated at least as many genes as QTL we were simulating and then randomly sampled genes annotated by that term. These genes were treated as quantitative trait genes and were used to seed the QTL. We then defined a QTL as the interval containing 20 Mb centered on the quantitative trait gene. We simulated data sets of two sizes, one containing three non-overlapping QTL and one containing six non-overlapping QTL. For both sizes, we generated 100 independent replicates. We defined power as the percent of replicates for which the true GO term was determined to be significantly enriched at an experiment-wide significance level α = 5.0%.
Fold-enrichment
Consider a QTL containing N total genes. In the absence of any information with which to prioritize genes within the QTL, genes can be arbitrarily ranked from 1 (highest) to N (lowest). Let ug represent the rank of the g-th gene, g = 1,2,…,N. The average rank for a gene is 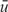 = (N + 1) / 2. In the presence of information with which to prioritize genes within the QTL, causal genes should move toward the top of the list. We defined fold-enrichment (FE) for the g-th gene in the QTL as the average rank of a gene before prioritization divided by the rank of the g-th gene after prioritization,
= (N + 1) / 2. In the presence of information with which to prioritize genes within the QTL, causal genes should move toward the top of the list. We defined fold-enrichment (FE) for the g-th gene in the QTL as the average rank of a gene before prioritization divided by the rank of the g-th gene after prioritization,
Plausibility analysis
Some GO terms that CFA identified as significantly enriched for a particular data set may have been previously associated with the relevant phenotype. To test the biological plausibility of the GO terms identified as significantly enriched, we assessed the co-occurrence of those terms in both the Entrez Gene and Online Mendelian Inheritance in Man (OMIM, http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?db=OMIM) databases. First, we searched the current records in Entrez Gene using the phenotype, GO term and organism. An example of such a query was ‘Alzheimer's and “membrane” [GO] and Homo sapiens’. We recorded all unique genes returned by this query. We repeated this search using all significantly enriched GO terms for a phenotype and compiled all genes into a single list. For each gene in this list, we reviewed its corresponding record in OMIM and searched for the occurrence of the relevant phenotype in the gene's description. The proportion of genes in OMIM associated with the phenotype among the genes in Entrez Gene also associated with the phenotype provides a measure of consistency across the two databases.
RESULTS
Characterization of the genome-wide GO term correlation matrix
In the 9 May 2006 release of the gene2go file, there were 16 114 unique human genes annotated by 5147 distinct GO terms. Annotations included 2308 molecular function terms, 548 cellular component terms and 2291 biological process terms. Among all pairs of GO terms, 99.27% of the correlation coefficients were negative and 0.73% were positive. This result indicated that for the vast majority of pairs of GO terms, explicit co-annotation with multiple terms is very uncommon.
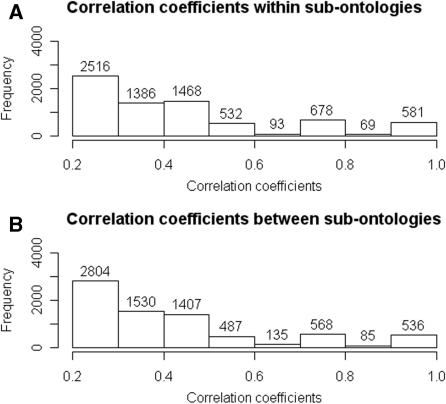
The smallest correlation coefficient was −0.287 and the largest correlation coefficient was 1. Figure 2 shows the distribution of correlation coefficients larger than 0.2. Annotation guidelines published on the GO web site advise annotators to consider the GO True Path rule when assigning annotations to gene products. Because annotation with a child term implies annotation by all parental terms, GO annotations for a given genome should not include examples of co-annotation by parents and their descendents. We counted 576 correlation coefficients equal to one for pairs of terms within the same sub-ontology. Only seven of these correlation coefficients involved terms in ancestor-descendent relationships. Among all correlation coefficients larger than 0.2 for pairs of terms within the same sub-ontology, 6.6% involved terms in ancestor-descendent relationships.
Figure 2.
Distributions of positive correlation coefficients. (A) Correlation coefficients >0.2 for term pairs in which both terms belong to the same sub-ontology. (B) Correlation coefficients >0.2 for term pairs in which the terms belong to different sub-ontologies.
There were more correlation coefficients larger than 0.2 between terms between sub-ontologies, which was surprising given disjoint sub-ontologies. A total of 515 correlation coefficients between terms between sub-ontologies were one. By definition, none of these correlation coefficients involved terms in ancestor-descendent relationships. Hence, ∼97% of large, positive correlation coefficients did not reflect ancestor-descendent relationships. Furthermore, these results indicated that 1091 GO terms were redundant, in the sense that annotation with one term implied annotation by the other in this vocabulary.
Assessment of the false positive error rate
To assess the validity of CFA, we generated data sets under the null hypothesis of no significant enrichment of GO terms. To generate a data set under the null hypothesis, we randomly sampled a nucleotide position from a randomly sampled chromosome. A QTL was defined as the 20 Mb region centered on the nucleotide position. To match the size of the Alzheimer's data set, we generated three QTL per simulated data set. We repeated this process to randomly generate 100 simulated data sets. On average, a data set contained 275 genes annotated by a total of 554 distinct GO terms.
We then assessed how many GO terms were declared significantly enriched by the CFA method. Since data were simulated under the null hypothesis, any finding of significant enrichment represents a false positive finding. Using a full Bonferroni correction (assuming independence among tests), the false positive error rate for enriched GO terms was 0.93%. Using a partial Bonferroni correction (accounting for correlated tests), the false positive error rate for enriched GO terms was 2.0%. Both of these false positive error rates were smaller than the experiment-wide significance level α=5.0%, indicating that there were too few rejections of the null hypothesis. Thus, both the full and partial Bonferroni corrections for multiple tests were conservative. Furthermore, the partial Bonferroni correction was less conservative than the full Bonferroni correction.
We then assessed how CFA behaves with larger data sets. We considered two approaches to increase the size of data sets: (i) increase the size of QTL or (ii) increase the number of QTL. To a wet-lab experimentalist, a larger QTL implies a loss of mapping resolution and is less likely to occur in studies utilizing whole-genome, high-throughput tools such as array- or bead-based SNP assays. On the other hand, the latter approach of increasing the number of QTL is more consistent with the genetics underlying complex traits, which are typically associated with multiple QTL. We therefore chose to implement the latter approach by doubling the number of simulated QTL per data set. We randomly generated 100 data sets, with each data set consisting of six randomly generated, unlinked QTL. Each QTL was 20 Mb long. On average, each data set contained 525 genes annotated by a total of 848 distinct GO terms. The false positive error rates using the full and partial Bonferroni corrections were 0.67 and 1.3%, respectively. These results indicated that both the full and partial Bonferroni corrections became increasingly conservative with larger data sets (i.e. as the number of tests increased) and that the partial Bonferroni correction remained less conservative than the full Bonferroni correction.
Assessment of power
In order to assess the power of CFA, we generated data sets under the alternative hypothesis of significant enrichment of GO terms among putative causal genes. To generate a data set under the alternative hypothesis, we first randomly sampled one GO term from all GO terms from the human annotation set. Then, we randomly sampled three genes annotated by that GO term to represent causal genes. As before, QTL were defined as 20 Mb regions centered on those genes. We repeated this process to randomly generate 100 simulated data sets for 100 randomly selected terms. We found that the randomly sampled GO term was significantly enriched in 71% of the simulations; that is, CFA successfully detected a true pattern of enrichment among genes under the three simulated QTL with 71% power.
We further assessed the ability of CFA to identify a causal gene among all genes within a QTL. CFA scores each gene in a QTL based on annotation by significantly enriched GO terms. Genes can be prioritized by ranking these scores. Based on rankings, the average enrichment was ∼12-fold across all replicates, that is, the average number of genes that would have to be experimentally tested before the causal gene was found was reduced ∼12-fold. This corresponded to causal genes being among the top 23% of ranked candidates, on average. One of the causal genes was the top-ranked gene in 14% of all simulated QTL sets. Conditional on the true GO term being significantly enriched, the average enrichment increased to ∼15-fold. This corresponded to causal genes being among the top 13% of ranked candidates, on average.
To assess the effect of larger data sets on power, we again doubled the number of simulated QTL per data set. We randomly sampled one GO term from all GO terms from the human annotation set and then we randomly sampled six genes annotated by that GO term to represent causal genes. QTL were defined as 20 Mb regions centered on those genes. We repeated this process to randomly generate 100 simulated data sets. The randomly sampled GO term was significantly enriched in 78% of the simulations. This result indicated that power increased with more information represented by sharing a GO term across more QTL, despite the increased conservativeness of controlling the false positive error rate when performing more tests in larger data sets. The average enrichment was ∼13-fold across all replicates. This corresponded to causal genes being among the top 22% of ranked candidates, on average. The causal gene was the top-ranked gene in 17% of all QTL. Conditional on the true GO term being significantly enriched, the average enrichment increased to ∼15-fold. This corresponded to causal genes being among the top 16% of ranked candidates, on average. Assuming that all causal genes exposed in multiple QTL conform to the expectation that they share some common annotation, these results demonstrate that CFA gains power as the number of QTL increases and therefore will work best with traits associated with greater numbers of QTL.
Application to QTL linked to Alzheimer's disease
We next applied the CFA method to an analysis of three QTL for age-of-onset of Alzheimer's disease (Table 1). These three QTL covered 449 genes, of which 341 were annotated by 629 GO terms; the remaining 108 genes were not annotated. Velicer's MAP test (22) performed on the correlation matrix for the 629 GO terms indicated that only 50 principal components were required to minimize the average squared partial correlation. We therefore adjusted the P-values from the 629 Fisher's exact tests using a partial Bonferroni correction for 50 tests. Of the 629 GO terms, 11 had adjusted P-values <0.05 and were therefore considered to be significantly enriched (Table 4). These 11 terms range from general to more specific annotations, spanning six levels of the GO hierarchies. Table S1 presents the list of 341 Alzheimer's candidate genes, sorted by QTL, and ranked by score within each QTL.
Table 4.
Significantly enriched Gene Ontology terms for Alzheimer's disease
| Term | Adjusted P-value |
|---|---|
| MHC class I protein complex | 0.0017 |
| Antigen presentation | 0.0020 |
| MHC class I receptor activity | 0.0057 |
| Integral to membrane | 0.0080 |
| Olfactory receptor activity | 0.0081 |
| Sensory perception of smell | 0.0087 |
| Palmitoyl-CoA hydrolase activity | 0.0090 |
| Estrogen receptor activity | 0.0223 |
| Photoreceptor cell maintenance | 0.0223 |
| Endoplasmic reticulum | 0.0321 |
| Membrane | 0.0398 |
The QTL at chromosome 6q27 illustrates the correlation of terms between sub-ontologies in this data set. The 11 significantly enriched terms included the biological process ‘antigen presentation’, the molecular function ‘MHC class I receptor activity’, and the cellular component ‘MHC class I protein complex’. Each of these three terms annotated each of six genes located at chromosome 6q27, including: retinoic acid early transcript 1E (RAET1E), retinoic acid early transcript 1G (RAET1G), retinoic acid early transcript 1L (RAET1L), the top-scoring gene in this QTL (Table S1) UL16 binding protein 1 (ULBP1, also known as RAET1I), UL16 binding protein 2 (ULBP2, also known as RAET1H) and UL16-binding protein 3 (ULBP3, also known as RAET1N).
The QTL at chromosome 11q25 was notable for containing many members of a multi-gene family encoding odorant receptors. Eighteen odorant receptor genes were tied for the top score, and two additional odorant receptor genes were tied for the second highest score (Table S1). No genes in the other two QTL were annotated with the molecular function ‘odorant receptor activity’ or the biological process ‘sensory perception of smell’, suggesting that significant enrichment of these two correlated terms may reflect gene duplication within this one QTL. An alternative candidate, SORL1 directs trafficking of amyloid precursor protein into recycling pathways and has recently been reported to be associated with late-onset Alzheimer's disease (23). The score for SORL1 was tied for sixth in rank (Table S1). The QTL at chromosome 14q22 may represent linkage to presenilin 1 (PSEN1). PSEN1 has been linked to early-onset Alzheimer's disease (24,25). The score for PSEN1 was tied for second in rank (Table S1).
One of the most straightforward methods of testing the biological plausibility of the GO terms identified as significantly enriched is to examine the co-occurrence of those terms along with the term ‘Alzheimer's’ in databases such as Entrez Gene and OMIM (Tables 5 and S2). For each significant term, we searched Entrez Gene using a query that retrieved records containing both the GO term and the keyword ‘Alzheimer's’. For example, querying Entrez Gene using the keyword ‘Alzheimer's’ and the GO term ‘membrane’ retrieved 113 human genes. Searches using the terms ‘integral to membrane’ and ‘endoplasmic reticulum’ in combination with ‘Alzheimer's’ retrieved 39 and 18 gene records, respectively. Of the 11 significantly enriched GO terms in Table 4, six co-occurred in Entrez Gene with ‘Alzheimer's’, yielding a total of 115 co-annotated human genes. These results indicated that these six significantly enriched GO terms have already been associated with Alzheimer's disease and represented confirmatory findings, and the other five represented novel findings, suggesting new hypotheses regarding the molecular basis of Alzheimer's disease. Cross-referencing the QTL locations (Table 1) with the chromosomal locations of these 115 genes (Tables 5 and S2) uncovered four additional candidate genes, including ESR1 at 6q25 (the score was 10th in rank), ESR2 at 14q23 (the score was 9th in rank), PTGER2 at 14q22 (the score was 10th in rank) and TMED10 at 14q22 (the score was 11th in rank) (Table S1).
Table 5.
Enriched GO terms cross-referenced with occurrence of term and Alzheimer's in Entrez Gene and OMIM among human genes
| GO Term | |||||||
|---|---|---|---|---|---|---|---|
| Gene | Membrane (113 total) | Integral to membrane (39 total) | Endoplasmic reticulum | Estrogen receptor | MHC Class 1 protein complex | Sensory perception of smell | Chromosome |
| APH1A | X | X | 1p36-q31 | ||||
| APP | X | X | X | 21q21 | |||
| BCHE | X | 3q26 | |||||
| CASP7 | X | X | 10q25 | ||||
| CYP19A1 | X | X | 15q21 | ||||
| CYP46A1 | X | X | X | 14q32 | |||
| CYP7B1 | X | X | 8q21 | ||||
| DHCR24 | X | X | X | 1p33-31 | |||
| ESR1 | X | X | 6q25 | ||||
| ESR2 | X | 14q23 | |||||
| GNAS | X | X | 20q13 | ||||
| HFE | X | X | 6p21 | ||||
| HMOX1 | X | X | 22q13 | ||||
| HSD17B10 | X | X | X | Xp11 | |||
| ITGB1 | X | X | X | 10p11 | |||
| NCSTN | X | X | 1q22-23 | ||||
| OPRS1 | X | X | 9p13 | ||||
| PRNP | X | X | 20p13 | ||||
| PSEN1 | X | X | 14q24 | ||||
| PSEN2 | X | X | X | 1q31-42 | |||
| PSENEN | X | X | 19q13 | ||||
| STX8 | X | X | 17p12 | ||||
The terms ‘antigen presentation’, ‘MHC Class I receptor activity’, ‘photoreceptor cell maintenance’, ‘olfactory’ and ‘palmitoyl-CoA hydrolase activity’ did not return any human genes containing the GO term and ‘Alzheimer's’ from Entrez Gene. Only a partial listing for genes annotated with ‘membrane’ or ‘integral to membrane’ is shown. Genes that contain ‘Alzheimer’ in their OMIM reference are indicated in bold. Chromosomal regions for genes that co-localize with QTL included in this study are indicated in bold italics.
Another source of confirmation of the biological plausibility is the occurrence of the term ‘Alzheimer’ in the Online Mendelian Inheritance in Man (OMIM) database for genes identified in the Entrez Gene analysis. For example, GNAS (annotated with significantly enriched GO terms ‘membrane’ and ‘sensory perception of smell’) does not co-occur with ‘Alzheimer’ in OMIM, whereas HFE (annotated with significantly enriched GO terms ‘membrane’ and ‘MHC Class I protein complex’) does co-occur with ‘Alzheimer’ (OMIM #104300). Of the 115 genes for which ‘Alzheimer’ and a significantly enriched GO term co-occurred in Entrez Gene, 44 were associated with ‘Alzheimer’ in OMIM (Tables 5 and S2). These results are encouraging in the sense of reliability across these two different databases, an important consideration given the currently incomplete states of the databases.
Application to QTL linked to BMI
We next analyzed a larger data set of QTL linked to BMI, which is a measure of obesity. A total of 18 QTL from 10 different studies were included in this analysis (Table 2). The QTL together included 2150 genes, of which 1655 were annotated by 1678 GO terms; the remaining 495 genes were not annotated. Analysis of the GO term co-annotation correlation matrix revealed that the GO terms were reducible to 140 principal components. After correcting for 140 effectively independent tests, 12 GO terms were significantly enriched (Table 6). These 12 terms span four levels of the GO hierarchies.
Table 6.
Significantly enriched Gene Ontology terms for body mass index
| Term | Adjusted P-value |
|---|---|
| Homophilic cell adhesion | 1.727e-23 |
| Calcium-dependent cell-cell adhesion | 1.366e-8 |
| Cell adhesion | 3.520e-8 |
| Transcription | 2.570e-6 |
| Regulation of transcription, DNA-dependent | 1.526e-6 |
| Synaptogenesis | 2.920e-5 |
| Protein binding | 2.932e-4 |
| Serine-type endopeptidase inhibitor activity | 0.0101 |
| Nucleus | 0.0133 |
| Metal ion binding | 0.0148 |
| Lipid binding | 0.0182 |
| Membrane | 0.0426 |
The list of 1655 genes, sorted by QTL and ranked by score within each QTL, is shown in Table S3. None of the top-scoring genes have been previously linked to BMI. Genes in all 18 QTL were annotated by the significantly enriched terms ‘metal ion binding’, ‘nucleus’, ‘regulation of transcription, DNA-dependent’, ‘membrane’, ‘transcription’, and ‘protein binding’. Based on these results, we hypothesize that multiple transcription factors are linked to BMI [for possible examples of other transcriptional regulators associated with BMI, see (26–28)]. The significantly enriched GO term ‘cell adhesion’ annotated genes in 16 of the 18 QTL. Three of the 16 QTL (5q32, 13q14 and 20q13) included members of the cadherin superfamily. Like the odorant receptors in the Alzheimer's disease data, the cadherin superfamily is notable for gene duplication (Table S3). For the QTL at chromosomes 5q32, 13q14 and 20q13, protocadherin or cadherin genes were the top-scoring genes. Since these three QTL were identified in three independent studies (Table 2), we suggest that this novel result is more likely to represent a true positive finding rather than a false positive finding and we therefore hypothesize that cadherin superfamily genes are also linked to BMI.
The results of the search for significantly enriched GO terms and ‘body mass index’ or ‘BMI’ in Entrez Gene are shown in Table 7. As with the Alzheimer's disease data, the more general GO terms such as ‘membrane’ returned the most genes co-annotated by the GO term along with ‘body mass index’ or ‘BMI’. Of the 12 significantly enriched GO terms in Table 6, nine co-occurred in Entrez Gene with disease terms ‘body mass index’ or ‘BMI’ for a total of 34 co-annotated human genes (Table 7). These results indicated that nine significantly enriched GO terms associated with BMI represented confirmatory findings and that CFA generated three novel findings. Comparing QTL locations (Table 2) with the chromosomal locations of these 34 genes (Table 7) revealed seven additional candidate genes, including TGFBI (the score was 9th in rank), ADRB2 (the score was 13th in rank) and NR3C1 (the score was 21st in rank) at 5q32; ESR1 (the score was 8th in rank) at 6q25; TNFRSF1B (the score was 7th in rank) at 1p36; IL6 at 7p21 (the score was 16th in rank) and LEP at 7q31 (the score was 17th in rank) (Table S3).
Table 7.
Enriched GO terms cross-referenced with occurrence of term body mass index or BMI in Entrez Gene and OMIM
| GO Term | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Gene | Metal ion binding | Nucleus | Regulation of transcription, DNA-dependent | Membrane | Transcription | Protein binding | Cell Adhesion | Serine-type endopeptidase inhibitor activity | Lipid binding | Chromosome |
| ACE | X | X | 17q23 | |||||||
| ADRB1 | X | X | 10q24-26 | |||||||
| ADRB2 | X | X | X | X | 5q31-32 | |||||
| ADRB3 | X | 8p11-12 | ||||||||
| AGT | X | 1q42-43 | ||||||||
| APOC3 | X | 11q23 | ||||||||
| BDNF | X | 11p13 | ||||||||
| CYP17A1 | X | 10q24 | ||||||||
| DGAT1 | X | 8q24 | ||||||||
| DRD4 | X | 11p15 | ||||||||
| ENPP1 | X | 6q22-23 | ||||||||
| ESR1 | X | X | X | X | X | X | X | 6q25 | ||
| IL1RN | X | 2q14 | ||||||||
| IL6 | X | 7p21 | ||||||||
| INS | X | 11p15 | ||||||||
| LEP | X | 7q31 | ||||||||
| LEPR | X | X | 1p31 | |||||||
| LPL | X | 8p22 | ||||||||
| MAOA | X | Xp11 | ||||||||
| NR3C1 | X | X | X | X | X | X | 5q31 | |||
| NTRK2 | X | X | 9q22 | |||||||
| PPARA | X | X | X | X | X | 22q13 | ||||
| PPARD | X | X | X | 6p21 | ||||||
| PPARG | X | X | X | X | X | 3p25 | ||||
| PPP1R3A | X | 7q31 | ||||||||
| SERPINE1 | X | X | 7q21-22 | |||||||
| SORBS1 | X | X | 10q23-24 | |||||||
| TFRC | X | 3q29 | ||||||||
| TGFBI | X | X | 5q31 | |||||||
| TNF | X | X | X | X | X | 6p21 | ||||
| TNFRSF1B | X | X | 1p36 | |||||||
| UCP1 | X | X | 4q31 | |||||||
| UCP3 | X | 11q13 | ||||||||
| VDR | X | X | X | X | X | 12q13 | ||||
The terms ‘homophilic cell adhesion’, ‘calcium-dependent cell–cell adhesion’, other more general related terms such as ‘calcium-dependent adhesion’, and ‘synaptogenesis’ did not return any hits when searched for co-occurrence with ‘body mass index’ or ‘BMI’ in Entrez Gene. Genes that contain ‘body mass index’ or ‘BMI’ in their OMIM reference are indicated in bold. Chromosomal regions for genes that co-localize with QTL included in this study are indicated in bold italics.
Of the 34 genes for which a significantly enriched GO term co-occurred with ‘body mass index’ or ‘BMI’ in Entrez Gene, 21 were associated with either ‘body mass index’ or ‘BMI’ in OMIM (Table 7). The level of co-annotation between Entrez Gene and OMIM for BMI (21/34 = 62%) was higher than the level of co-annotation between Entrez Gene and OMIM for Alzheimer's disease (44/115 = 38%), indicating a higher degree of concordance between Entrez Gene and OMIM for previously suspected candidate genes for BMI.
DISCUSSION
In this study, we describe CFA, a method for prioritizing candidate genes from genome-wide linkage studies. The fundamental assumption of the method is that genes linked to a complex trait are more likely to share annotation (such as GO annotation) than genes chosen at random, such that some shared annotations will be enriched among genes linked to the trait. Of 163 genes involved in 29 diseases for which at least three genes are reported to affect risk, 80% shared an annotation with another gene for the same disease (29). Researchers have taken advantage of this enrichment to identify genes involved in breast cancer (30). Ritchie et al. (31) identified four SNPs in three genes from the estrogen metabolism pathway that are strongly associated with sporadic breast cancer. Pathway information has been used to identify candidate genes in expression-based studies for autism (32) and prostate cancer (33). Recently, a follow-up study to the identification of the involvement of complement factor H in age-related macular degeneration (34) identified several SNPs in the complement pathway, indicating that other genes in the complement pathway besides factor H may be involved in this disease (35). On the other hand, it is possible that complex traits are characterized by genetic heterogeneity such that annotations are not enriched among genes correlated to the same trait. For such traits, CFA is a valid statistical procedure in the sense that the false positive error rate is properly controlled, but will have no power to detect true positives.
CFA utilizes principal components analysis to account for the correlation structure both within and between the three GO sub-ontologies. Furthermore, since the genome-wide correlation matrix is constructed by considering all possible pairs of terms, CFA is completely independent of the location of terms within the GO hierarchy, allowing terms to be compared regardless of their generality. We test for enrichment of GO terms using Fisher's exact test. We stress that the unit of testing is a GO term and not a gene. Principal components analysis further allows for dimension reduction, thereby mitigating multiple testing. As the GO hierarchy acquires more terms and the level of annotation of human gene products deepen, the problems related to multiple hypothesis testing will become more severe, thus increasing the need for estimating the true number of independent tests using the PCA approach presented here. As an additional benefit, the principal components analysis can be used in conjunction with any term-by-term test, not just Fisher's exact test. We develop a scoring function in which a gene score is determined by the presence or absence of annotation by significantly enriched GO terms for that gene. Genes annotated with more significantly enriched GO terms have higher scores. Genes can be prioritized by ranking them on the basis of their scores in descending order, such that genes with higher scores receive higher priority. We tested CFA using simulated data and found that it was conservative (in our opinion, acceptably so for an exploratory, data-mining task), but had good power. We used this method to prioritize candidate genes for QTL linked to two complex traits, Alzheimer's disease and BMI (Tables S1 and S3, respectively).
To our knowledge, CFA is the first method to use principal components analysis to account for the correlation structure among all GO terms. In concept, this approach is similar to the use of principal components analysis of gene expression data for groups of genes (36–38). The correlation structure among GO terms affects analysis in two ways: (i) tests for enrichment for individual GO terms are dependent and (ii) weights for GO terms in the gene scores are correlated. Several methods have been developed that account for dependencies within sub-ontologies but do not (as yet) account for dependencies between sub-ontologies (39–43). For gene expression data, Delongchamp et al. (44) developed a meta-analytic method to combine P-values that accounts for the correlation of P-values within a group of genes defined by a single GO term but does not account for correlation among groups. Several groups have developed resampling-based procedures to assess significance (37,45). Permutation testing and bootstrapping of gene expression data do not require estimation of the correlation structure but are computationally expensive. Pinto et al. (46) used bootstrapping to assess significance of correlation coefficients between distance measures for gene expression and annotation measures. Our use of Velicer's MAP test to achieve dimension reduction and the use of this dimension reduction to mitigate multiple testing appears to be novel. Velicer's MAP test has a statistically justified basis and does not require subjective thresholding in terms of the proportion of variance explained when determining the number of principal components to retain (22).
Bioinformatic methods for identifying candidate genes employing GO annotation include SUSPECTS (47,48), G2D (49,50) and POCUS (29). Of these methods, CFA is most similar to POCUS. In contrast to SUSPECTS and G2D, POCUS and CFA do not require training sets. A critical limitation of training sets is that only candidate genes sharing annotation with training genes can be detected; true candidate genes not sharing annotation with training genes cannot be detected. POCUS bases it score on the frequency with which genes from more than one locus share a given annotation. POCUS's power was estimated to be 65% for data sets containing an average of 20 genes, 19% for data sets containing an average of 94 genes and 15% for data sets containing an average of 187 genes (29). In comparison, CFA's power was estimated to be 71% for data sets containing three loci of ∼130 genes each and 78% for data sets containing six loci of ∼137 genes each. Whereas POCUS loses power as the size of the data set increases, CFA gains power. A full Bonferroni correction is more conservative than a partial Bonferroni correction, and this difference increases with larger data sets. By accounting for correlations among GO terms, a partial Bonferroni correction based on principal components analysis of the correlation matrix effectively preserves power for larger data sets. Furthermore, for similarly sized data sets, CFA appears to be substantially more powerful than POCUS. POCUS requires more than one susceptibility locus; CFA works with any number of susceptibility loci. POCUS further assumes sharing events (i.e. GO terms) are independent; CFA explicitly accounts for two sources of correlation among GO terms.
We applied the CFA method to the results from studies investigating the genetic basis of two different quantitative traits: BMI and age-of-onset for Alzheimer's disease. Our analyses revealed several previously known candidate genes and proposed several new candidate genes influencing these traits. However, our findings may represent false positives, and we give five reasons for why this might be the correct explanation. First, QTL reported in the original studies might be false positives. Our simulation demonstrated that CFA retained validity in the absence of true positive QTL, so this possibility is unlikely. Second, genes may be incorrectly located on the current assembly of the human genome. Third, given the low resolution of linkage studies, a region of 20 Mb centered on the nearest significant marker may have missed the true linked gene(s). Given that significant linkage indicates either QTL with small effects close to the marker or QTL with large effects distant from the marker, and given that complex traits generally involve many loci with small effects, we believe this possibility to be unlikely. Fourth, the annotation of genes in GO is incomplete and biased toward highly studied genes; thus, novel or poorly characterized genes could be missed. Fifth, significantly small P-values from Fisher's exact test might represent false positives, even after correcting for multiple tests. Our simulation indicated that power to detect true patterns of enriched GO terms is >70%, strongly suggesting that the candidate genes reported here may represent true positives.
A recurrent finding of CFA is that significant enrichment of GO terms appears to result from linkage of genes from the same family arising from gene duplication. Duplication can give rise to genes in the same QTL that are more likely to share annotations than are unrelated genes. If one QTL contains many such duplicates, the associated annotations may remain significantly enriched even when combined across multiple QTL. This phenomenon may apply to the antigen presentation genes and odorant receptor genes for Alzheimer's disease and the cadherin superfamily genes forBMI. In the former two cases, relevant GO terms annotated genes in only one QTL, and we may be more inclined to believe that significant enrichment resulted solely from gene duplication. In contrast, in the latter case, cell adhesion GO terms annotated genes in 16 of 18 QTL, with QTL derived from multiple studies, and we may be more inclined to believe that significant enrichment resulted from true commonality. A possible implication of these findings is that QTL for complex traits may tend to contain gene duplicates, such that the duplication may be a predictive correlate to disease susceptibility (51).
Candidate genes associated with Alzheimer's disease have been identified for the QTL at 11q25 (SORL1) (23) and 14q22 (PSEN1) (24,25). No clear identification of candidate genes exists for the QTL at 6q27. Based on our results, we hypothesize that candidate genes at this QTL may affect age-on-onset via MHC class I antigen presentation. Interestingly, ULBP expression renders cells sensitive to cytotoxicity mediated by natural killer cells and is blocked by human cytomegalovirus glycoprotein UL16 (52). At this time, it is unclear if this process reflects infection, possibly with a herpesvirus (53), or an autoimmunity-related phenomenon.
For the BMI data, none of the top-scoring genes has been previously associated with this quantitative trait. We observed two potentially meaningful groupings of significantly enriched GO terms. One group annotated transcription factors and the other group annotated cell adhesion molecules. Cell adhesion is the biological process defined as ‘the attachment of a cell, either to another cell or to an underlying substrate such as the extracellular matrix, via cell adhesion molecules’ (http://www.godatabase.org). For these GO terms, several of the top-scoring genes are members of the cadherin superfamily. According to Entrez Gene, cadherin superfamily genes, such as PCDH17, PCDH20, CDH22 and PCDHB7, are speculated to affect cell–cell neural connections. Based on our results, we hypothesize that there may be an association between BMI and genes in the cadherin superfamily. In support of this hypothesis, the cadherin gene fat was recently found to affect organ size in Drosophila (54).
There are many possible extensions to this work. First, more linkage studies could be examined, and a scheme that weights for replicability of QTL across studies could be devised. Second, GO annotations are accompanied by evidence codes that also have a hierarchical structure of reliability. A weighting scheme that incorporates this information could be devised [for one example see (55)]. Third, tests for composite annotation could be investigated (56). Fourth, additional sources of information such as gene expression, protein–protein interaction networks, tissue specificity, KEGG or BioCarta pathways and sequence homology, could be integrated into a combined statistic in a manner similar to Maestro (57) or Endeavour (58). For these types of integrative methods, it is critical to account for the covariance of the different data sources. Principal components analysis provides a way to account for covariance while also allowing for dimension reduction. Fifth, biological confirmation of the candidate genes should be performed. Sixth, more powerful methods of correcting for multiple tests could be implemented (59). Interestingly, for both real data analyses, the partial Bonferroni correction and the Benjamini–Hochberg false discovery rate yield the same number of rejected null hypotheses (data not shown), suggesting that these two post hoc methods are comparably powerful. Seventh, by taking advantage of extensive GO annotations available for multiple species, we have generated genome-wide GO term correlation matrices for Arabidopsis thaliana, Drosophila melanogaster, Mus musculus and Saccharomyces cerevisiae. Thus, CFA can be readily applied to linkage data from these model organisms.
Taken together, our work has generated a promising new set of candidate genes that may assist in defining genetic factors linked to Alzheimer's disease and BMI. If confirmed, these genes may offer new targets for diagnosis and treatment. More broadly, CFA can generate a prioritized set of candidate genes that may assist in defining genes linked to complex traits.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
ACKNOWLEDGEMENTS
We thank Jasmin Divers for assistance in porting code for Velicer's minimum average partial test from SAS to R. We thank the anonymous reviewers for their comments, which helped to improve this manuscript. Funds were provided by National Institutes of Health (DK062710, AR052658-03S1, CA100949 and AR007450). Funding to pay the Open Access publication charges for this article was provided by National Institutes of Health grant DK062710.
Conflict of interest statement. None declared.
REFERENCES
- 1.Lynch M, Walsh B. Genetics and Analysis of Quantitative Traits. Inc., Sunderland, MA: Sinauer Associates; 1998. [Google Scholar]
- 2.Badano JL, Katsanis N. Beyond Mendel: an evolving view of human genetic disease transmission. Nat. Rev. Genet. 2002;3:779–789. doi: 10.1038/nrg910. [DOI] [PubMed] [Google Scholar]
- 3.Tiffin N, Adie E, Turner F, Brunner HG, van Driel MA, Oti M, López-Bigas N, Ouzounis C, Perez-Iratxeta C, Andrade-Navarro MA, et al. Computational disease gene identification: a concert of methods prioritizes type 2 diabetes and obesity candidate genes. Nucleic Acids Res. 2006;34:3067–3081. doi: 10.1093/nar/gkl381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight SS, Eppig JT, et al. Gene ontology: tool for the unification of biology. Nat. Genet. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Khatri P, Drăghici S. Ontological analysis of gene expression data: current tools, limitations, and open problems. Bioinformatics. 2005;21:3587–3595. doi: 10.1093/bioinformatics/bti565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Curtis RK, Orešič M, Vidal-Puig A. Pathways to the analysis of microarray data. Trends Biotechnol. 2005;23:429–435. doi: 10.1016/j.tibtech.2005.05.011. [DOI] [PubMed] [Google Scholar]
- 7.Rivals I, Personnaz L, Taing L, Potier M-C. Enrichment or depletion of a GO category within a class of genes: which test? Bioinformatics. 2007;23:401–407. doi: 10.1093/bioinformatics/btl633. [DOI] [PubMed] [Google Scholar]
- 8.Blacker D, Bertram L, Saunders AJ, Moscarillo TJ, Albert MS, Wiener H, Perry RT, Collins JS, Harrell LE, Go RC, et al. Results of a high-resolution genome screen of 437 Alzheimer's disease families. Hum. Mol. Genet. 2003;12:23–32. doi: 10.1093/hmg/ddg007. [DOI] [PubMed] [Google Scholar]
- 9.Hunt SC, Abkevich V, Hensel CH, Gutin A, Neff CD, Russell DL, Tran T, Hong X, Jammulapati S, Riley R, et al. Linkage of body mass index to chromosome 20 in Utah pedigrees. Hum. Genet. 2001;109:279–285. doi: 10.1007/s004390100581. [DOI] [PubMed] [Google Scholar]
- 10.Bell CG, Benzinou M, Siddiq A, Lecoeur C, Dina C, Lemainque A, Clément K, Basdevant A, Guy-Grand B, Mein CA, et al. Genome-wide linkage analysis for severe obesity in French Caucasians finds significant susceptibility locus on chromosome 19q. Diabetes. 2004;53:1857–1865. doi: 10.2337/diabetes.53.7.1857. [DOI] [PubMed] [Google Scholar]
- 11.Li X, Wang D, Yang K, Guo X, Lin Y-C, Samayoa CG, Yang H. Genome-wide linkage analysis using cross-sectional and longitudinal traits for body mass index in a subsample of the Framingham heart study. BMC Genet. 2003;4(Suppl. 1):S35. doi: 10.1186/1471-2156-4-S1-S35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Atwood LD, Heard-Costa NL, Cupples LA, Jaquish CE, Wilson PW, D'Agostino RB. Genomewide linkage analysis of body mass index across 28 years of the Framingham heart study. Am. J. Hum. Genet. 2002;71:1044–1050. doi: 10.1086/343822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Feitosa MF, Borecki IB, Rich SS, Arnett DK, Sholinsky P, Myers RH, Leppert M, Province MA. Quantitative-trait loci influencing body-mass index reside on chromosomes 7 and 13: the national heart, lung, and blood institute family heart study. Am. J. Hum. Genet. 2002;70:72–82. doi: 10.1086/338144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hager J, Dina C, Francke S, Dubois S, Houari M, Vatin V, Vaillant E, Lorentz N, Basdevant A, Clément K, et al. A genome-wide scan for human obesity genes reveals a major susceptibility locus on chromosome 10. Nat. Genet. 1998;20:304–308. doi: 10.1038/3123. [DOI] [PubMed] [Google Scholar]
- 15.Heijmans BT, Beem AL, Willemsen G, Posthuma D, Slagboom PE, Boomsma D. Further evidence for a QTL influencing body mass index on chromosome 7p from a genome-wide scan in Dutch families. Twin Res. 2004;7:192–196. doi: 10.1375/136905204323016177. [DOI] [PubMed] [Google Scholar]
- 16.Lewis CE, North KE, Arnett D, Borecki IB, Coon H, Ellison RC, Hunt SC, Oberman A, Rich SS, Province MA, et al. Sex-specific findings from a genome-wide linkage analysis of human fatness in non-Hispanic whites and African Americans: The HyperGEN study. Int. J. Obes. 2005;29:639–649. doi: 10.1038/sj.ijo.0802916. [DOI] [PubMed] [Google Scholar]
- 17.Beck SR, Brown WM, Williams AH, Pierce J, Rich SS, Langefeld CD. Age-stratified QTL genome scan analyses for anthropometric measures. BMC Genet. 2003;4(Suppl. 1):S31. doi: 10.1186/1471-2156-4-S1-S31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Deng H-W, Deng H, Liu Y-J, Liu Y-Z, Xu F-H, Shen H, Conway T, Li J-L, Huang Q-Y, Davies KM, et al. A genomewide linkage scan for quantitative-trait loci for obesity phenotypes. Am. J. Hum. Genet. 2002;70:1138–1151. doi: 10.1086/339934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Darvasi A, Weinreb A, Minke V, Weller JI, Soller M. Detecting marker-QTL linkage and estimating QTL gene effect and map location using a saturated genetic map. Genetics. 1993;134:943–951. doi: 10.1093/genetics/134.3.943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Karolchik D, Baertsch R, Diekhans M, Furey TS, Hinrichs A, Lu YT, Roskin KM, Schwartz M, Sugnet CW, Thomas DJ, et al. The UCSC genome browser database. Nucleic Acids Res. 2003;31:51–54. doi: 10.1093/nar/gkg129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.O'Connor BP. SPSS and SAS programs for determining the number of components using parallel analysis and Velicer's MAP test. Behav. Res. Methods, Instrum. Comput. 2000;32:396–402. doi: 10.3758/bf03200807. [DOI] [PubMed] [Google Scholar]
- 22.Velicer WF. Determining the number of components from the matrix of partial correlations. Psychometrika. 1976;41:321–327. [Google Scholar]
- 23.Rogaeva E, Meng Y, Lee JH, Gu Y, Kawarai T, Zou F, Katayama T, Baldwin CT, Cheng R, Hasegawa H, et al. The neuronal sortilin-related receptor SORL1 is genetically associated with Alzheimer disease. Nat. Genet. 2007;39:168–177. doi: 10.1038/ng1943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rogaeva EA, Fafel KC, Song YQ, Medeiros H, Sato C, Liang Y, Richard E, Rogaev EI, Frommelt P, Sadovnick AD, et al. Screening for PS1 mutations in a referral-based series of AD cases: 21 novel mutations. Neurology. 2001;57:621–625. doi: 10.1212/wnl.57.4.621. [DOI] [PubMed] [Google Scholar]
- 25.van Duijn CM, Cruts M, Theuns J, Van Gassen G, Backhovens H, van den Broeck M, Wehnert A, Serneels S, Hofman A, Van Broeckhoven C. Genetic association of the presenilin-1 regulatory region with early-onset Alzheimer's disease in a population-based sample. Eur. J. Hum. Genet. 1999;7:801–806. doi: 10.1038/sj.ejhg.5200373. [DOI] [PubMed] [Google Scholar]
- 26.Bell CG, Walley AJ, Froguel P. The genetics of human obesity. Nat. Rev. Genet. 2005;6:221–234. doi: 10.1038/nrg1556. [DOI] [PubMed] [Google Scholar]
- 27.Özcan U, Cao Q, Yilmaz E, Lee A-H, Iwakoshi NN, Özdelen E, Tuncman G, Görgün C, Glimcher LH, Hotamisligil GS. Endoplasmic reticulum stress links obesity, insulin action, and type 2 diabetes. Science. 2004;306:457–461. doi: 10.1126/science.1103160. [DOI] [PubMed] [Google Scholar]
- 28.Rankinen T, Zuberi A, Chagnon YC, Weisnagel SJ, Argyropoulos G, Walts B, Pérusse L, Bouchard C. The human obesity gene map: the 2005 update. Obesity. 2006;14:529–644. doi: 10.1038/oby.2006.71. [DOI] [PubMed] [Google Scholar]
- 29.Turner FS, Clutterbuck DR, Semple CA. POCUS: mining genomic sequence annotation to predict disease genes. Genome Biol. 2003;4:R75. doi: 10.1186/gb-2003-4-11-r75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kristensen VN, Edvardsen H, Tsalenko A, Nordgard SH, Sorlie T, Sharan R, Vailaya A, Ben-Dor A, Lonning PE, Lien S, et al. Genetic variation in putative regulatory loci controlling gene expression in breast cancer. Proc. Natl Acad. Sci. USA. 2006;103:7735–7740. doi: 10.1073/pnas.0601893103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ritchie MD, Hahn LW, Roodi N, Bailey LR, Dupont WD, Parl FF, Moore JH. Multifactor-dimensionality reduction reveals high-order interactions among estrogen-metabolism genes in sporadic breast cancer. Am. J. Hum. Genet. 2001;69:138–147. doi: 10.1086/321276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yonan AL, Palmer AA, Smith KC, Feldman I, Lee HK, Yonan JM, Fischer SG, Pavlidis P, Gilliam TC. Bioinformatic analysis of autism positional candidate genes using biological databases and computational gene network prediction. Genes, Brain Behav. 2003;2:303–320. doi: 10.1034/j.1601-183x.2003.00041.x. [DOI] [PubMed] [Google Scholar]
- 33.Manoli T, Gretz N, Grone HJ, Kenzelmann M, Eils R, Brors B. Group testing for pathway analysis improves comparability of different microarray datasets. Bioinformatics. 2006;22:2500–2506. doi: 10.1093/bioinformatics/btl424. [DOI] [PubMed] [Google Scholar]
- 34.Klein RJ, Zeiss C, Chew EY, Tsai JY, Sackler RS, Haynes C, Henning AK, SanGiovanni JP, Mane SM, Mayne ST, et al. Complement factor H polymorphism in age-related macular degeneration. Science. 2005;308:385–389. doi: 10.1126/science.1109557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dinu V, Miller PL, Zhao H. Evidence for association between multiple complement pathway genes and AMD. Genet. Epidemiol. 2007;31:224–237. doi: 10.1002/gepi.20204. [DOI] [PubMed] [Google Scholar]
- 36.Jiang Z, Gentleman R. Extensions to gene set enrichment. Bioinformatics. 2007;23:306–313. doi: 10.1093/bioinformatics/btl599. [DOI] [PubMed] [Google Scholar]
- 37.Kong SW, Pu WT, Park PJ. A multivariate approach for integrating genome-wide expression data and biological knowledge. Bioinformatics. 2006;22:2373–2380. doi: 10.1093/bioinformatics/btl401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kustra R, Shioda R, Zhu M. A factor analysis model for functional genomics. BMC Bioinformatics. 2006;7:216. doi: 10.1186/1471-2105-7-216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Falcon S, Gentleman R. Using GOstats to test gene lists for GO term association. Bioinformatics. 2007;23:257–258. doi: 10.1093/bioinformatics/btl567. [DOI] [PubMed] [Google Scholar]
- 40.Kirac M, Ozsoyoglu G, Yang J. Annotating proteins by mining protein interaction networks. Bioinformatics. 2006;22:e260–e270. doi: 10.1093/bioinformatics/btl221. [DOI] [PubMed] [Google Scholar]
- 41.Alexa A, Rahnenführer J, Lengauer T. Improved scoring of functional groups from gene expression data by decorrelating GO graph structure. Bioinformatics. 2006;22:1600–1607. doi: 10.1093/bioinformatics/btl140. [DOI] [PubMed] [Google Scholar]
- 42.Brameier M, Wiuf C. Co-clustering and visualization of gene expression data and gene ontology terms for Saccharomyces cerevisiae using self-organizing maps. J. Biomed. Inform. 2007;40:160–173. doi: 10.1016/j.jbi.2006.05.001. [DOI] [PubMed] [Google Scholar]
- 43.Sevilla JL, Segura V, Podhorski A, Guruceaga E, Mato JM, Martínez-Cruz LA, Corrales FJ, Rubio A. Correlation between gene expression and GO semantic similarity. IEEE/ACM Trans. Comput. Biol. Bioinform. 2005;2:330–338. doi: 10.1109/TCBB.2005.50. [DOI] [PubMed] [Google Scholar]
- 44.Delongchamp R, Lee T, Velasco C. A method for computing the overall statistical significance of a treatment effect among a group of genes. BMC Bioinformatics. 2006;7(Suppl. 2):S11. doi: 10.1186/1471-2105-7-S2-S11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Barry WT, Nobel AB, Wright FA. Significance analysis of functional categories in gene expression studies: a structured permutation approach. Bioinformatics. 2005;21:1943–1949. doi: 10.1093/bioinformatics/bti260. [DOI] [PubMed] [Google Scholar]
- 46.Pinto FR, Cowart LA, Hannun YA, Rohrer B, Almeida JS. Local correlation of expression profiles with gene annotations - proof of concept for a general conciliatory method. Bioinformatics. 2005;21:1037–1045. doi: 10.1093/bioinformatics/bti074. [DOI] [PubMed] [Google Scholar]
- 47.Adie EA, Adams RR, Evans KL, Porteous DJ, Pickard BS. Speeding disease gene discovery by sequence based candidate prioritization. BMC Bioinformatics. 2005;6:55. doi: 10.1186/1471-2105-6-55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Adie EA, Adams RR, Evans KL, Porteous DJ, Pickard BS. SUSPECTS: enabling fast and effective prioritization of positional candidates. Bioinformatics. 2006;22:773–774. doi: 10.1093/bioinformatics/btk031. [DOI] [PubMed] [Google Scholar]
- 49.Perez-Iratxeta C, Bork P, Andrade MA. Association of genes to genetically inherited diseases using data mining. Nat. Genet. 2002;31:316–319. doi: 10.1038/ng895. [DOI] [PubMed] [Google Scholar]
- 50.Perez-Iratxeta C, Wjst M, Bork P, Andrade MA. G2D: a tool for mining genes associated with disease. BMC Genet. 2005;6:45. doi: 10.1186/1471-2156-6-45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.López-Bigas N, Ouzounis CA. Genome-wide identification of genes likely to be involved in human genetic disease. Nucleic Acids Res. 2004;32:3108–3114. doi: 10.1093/nar/gkh605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Sutherland CL, Chalupny NJ, Schooley K, VandenBos T, Kubin M, Cosman D. UL16-binding proteins, novel MHC class I-related proteins, bind to NKG2D and activate multiple signaling pathways in primary NK cells. J. Immunol. 2002;168:671–679. doi: 10.4049/jimmunol.168.2.671. [DOI] [PubMed] [Google Scholar]
- 53.Itzhaki RF, Wozniak MA. Herpes simplex virus type 1, apolipoprotein E, and cholesterol: a dangerous liaison in Alzheimer's disease and other disorders. Prog. Lipid Res. 2006;45:73–90. doi: 10.1016/j.plipres.2005.11.003. [DOI] [PubMed] [Google Scholar]
- 54.Bennett FC, Harvey KF. Fat cadherin modulates organ size in Drosophila via the Salvador/Warts/Hippo signaling pathway. Curr. Biol. 2006;16:2101–2110. doi: 10.1016/j.cub.2006.09.045. [DOI] [PubMed] [Google Scholar]
- 55.Popescu M, Keller JM, Mitchell JA. Fuzzy measures on the gene ontology for gene product similarity. IEEE/ACM Trans. Comput. Biol. Bioinform. 2006;3:263–274. doi: 10.1109/TCBB.2006.37. [DOI] [PubMed] [Google Scholar]
- 56.Nam D, Kim S-B, Kim S-K, Yang S, Kim S-Y, Chu I-S. ADGO: analysis of differentially expressed gene sets using composite GO annotation. Bioinformatics. 2006;22:2249–2253. doi: 10.1093/bioinformatics/btl378. [DOI] [PubMed] [Google Scholar]
- 57.Calvo S, Jain M, Xie X, Sheth SA, Chang B, Goldberger OA, Spinazzola A, Zeviani M, Carr SA, Mootha VK. Systematic identification of human mitochondrial disease genes through integrative genomics. Nat. Genet. 2006;38:576–582. doi: 10.1038/ng1776. [DOI] [PubMed] [Google Scholar]
- 58.Aerts S, Lambrechts D, Maity S, Van Loo P, Coessens B, De Smet F, Tranchevent L-C, De Moor B, Marynen P, Hassan B, et al. Gene prioritization through genomic data fusion. Nat. Biotechnol. 2006;24:537–544. doi: 10.1038/nbt1203. [DOI] [PubMed] [Google Scholar]
- 59.Storey JD. A direct approach to false discovery rates. J. Roy. Stat. Soc. Ser. B. 2002;64:479–498. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.