Abstract
Cells regulate gene expression using a complex network of signaling pathways, transcription factors and promoters. To gain insight into the structure and function of these networks we analyzed gene expression in single and multiple mutant strains to build a quantitative model of the Hog1 MAPK-dependent osmotic stress response in budding yeast. Our model reveals that the Hog1 and general stress (Msn2/4) pathways interact, at both the signaling and promoter level, to integrate information and create a context-dependent response. This study lays out a path to identifying and characterizing the role of signal integration and processing in other gene regulatory networks.
A full understanding of gene regulation will require the construction of detailed circuit diagrams that describe how signals influence transcription factor (TF) activity and how these TFs cooperate to regulate mRNA levels1,2. However, current experimental approaches used to examine these networks, such as chromatin immunoprecipitation (ChIP) and microarray analysis of strains with a single network component deleted3–6, provide only a limited view of their structure and function.
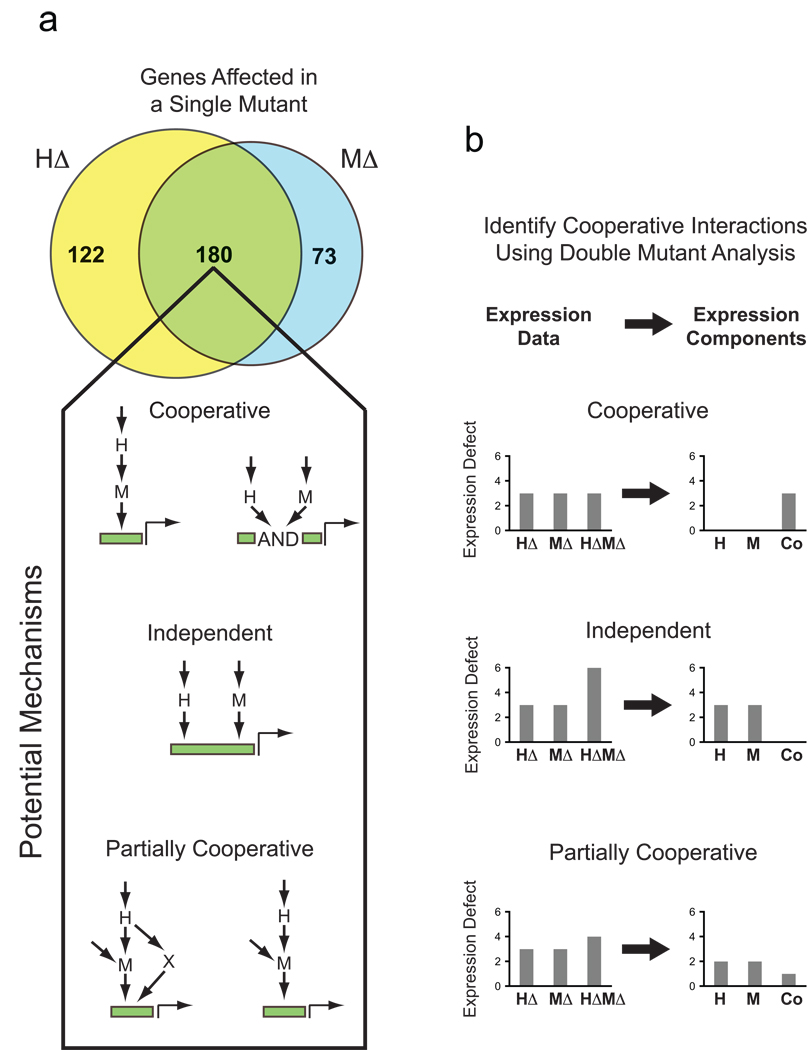
For example, when single mutant analysis is used, an interaction between two network components is inferred if they regulate overlapping gene-sets (e.g. HΔ and MΔ, Fig. 1a). However, it is not possible to tell from single-mutant data if two factors act fully cooperatively, independently, or partially cooperatively to regulate gene expression (Potential Mechanisms, Fig. 1a). Moreover, the nature of the interaction could vary from one target gene to another. As a result, network models derived from such data are incomplete and likely inaccurate.
Fig. 1.
Single and double mutant analysis of gene expression. (A) Venn diagram summarizing the overlap in the number of genes with a >2-fold (log2=1) defect in gene expression in the hog1Δ (HΔ) and msn2Δ msn4Δ (MΔ) mutants, following salt induction. Wiring diagrams indicate the possible ways factors H and M can interact to regulate expression of overlapping sets of genes. (B) Schematic illustrating the application of the double mutant approach to analyzing transcriptional network structure and function (see text for details).
To overcome this problem, and distinguish between possible regulatory mechanisms, double mutant (or epistasis) analysis can be applied7. Here, if two network components H and M act cooperatively to regulate a gene, then the single mutants (HΔ and MΔ) and double mutants (HΔMΔ) will have identical expression defects (Cooperative Mechanism, Fig. 1b). By contrast, if H and M act independently, then the expression defect in the double mutant will be the sum of the defects found in the single mutants (Independent Mechanism, Fig. 1b). In mechanisms with partial cooperativity, the observed behavior will lie between that found for cooperative and independent mechanisms (Partially Cooperative Mechanism, Fig. 1b). This approach has been used previously in conjunction with microarrays to examine regulatory mechanisms and pathway interactions at a coarse-grained or qualitative level5,8–12.
Here we show that double mutant analysis can be used to build a detailed and quantitative model of transcriptional regulation, including the strength and type of each edge in the network and the logic gate at each node (in a given condition). To achieve this goal, we developed a microarray-based strategy that allows us to overcome the significant noise in microarray measurements and accurately quantify the influence and interaction of network factors at individual genes. To do this we calculate the value of what we term the expression components for each gene. In the example of the interacting factors H and M, there are three such expression components (Fig. 1b, Expression Components column): the activation from H alone (H component); the activation from M alone (M component); and the activation that results from the interaction between H and M (Co component). These values are determined using a mutant cycle (similar to the mutant cycles used to probe inter- and intra-molecular protein interactions13, see Supplement) where we directly compare the expression in the wild-type, single, and double mutant strains (arrays C–F, Fig. 2a). We calculate the expression component values for each gene by regression using the equations that describe the expression components measured in each microarray (Fig. 2a, equations and Methods). Finally, we estimate the statistical significance of each expression component at each gene with a null hypothesis of <1.5-fold regulation, using the variance calculated in the global fit (see Methods and Supplement).
Fig. 2.
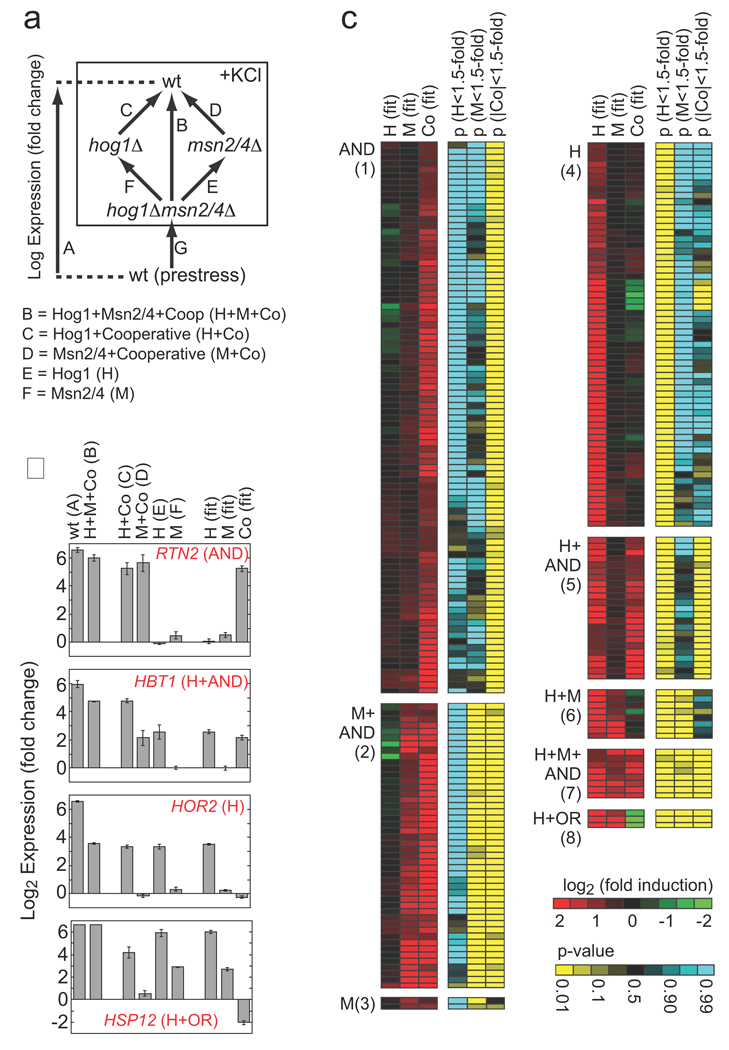
Role of Hog1 and Msn2/4 in osmotic stress-dependent gene induction. (A) Schema describing the experiments and equations used to break the influence of Hog1 and Msn2/4 into components. Each arrow represents a single microarray (measured in triplicate) comparing gene expression in two strains. The equations listed below the diagram describe the relationship between the data from each measurement and the underlying expression components. Note here that expression is in Log terms and thus an OR gate is manifest as a negative cooperative component equal to the H or M component (see Supplement). (B) Sample data for four genes showing the errors associated with the microarray measurements and expression component values. (C) Heat map showing the best-fit value of the expression components (red/green), and their statistical significance (yellow/blue), for all genes that are upregulated more than 3-fold in response to hyperosmotic stress, by Hog1 or Msn2/4 (>2-fold). Each row of six columns shows the data for a single gene. Genes are placed into groups (1–8) and labeled according to the combination of expression components (p<0.05 cut-off) that influence their induction (AND = +Co, OR = −Co). Data is not shown for 15 genes that are induced in the wild-type strain (>3 fold) by Hog1 and/or Msn2/4 (>2-fold) but have no significant expression component. See Tables S2 and S3 for full data.
We apply our strategy to analyze the regulatory network responsible for the hyper-osmotic stress response in budding yeast. In osmotic stress, the mitogen activated protein kinase (MAPK) Hog1 and the paralogous (general stress) TFs Msn2 and Msn4 are transported into the nucleus14 where, together, they activate a transcriptional program involving hundreds of genes (Fig. 1a, Venn diagram and Ref 15). Studies of strains lacking Hog1 or Msn2/4 have led to a model in which Msn2 and Msn4 function downstream of Hog1 in the osmotic stress response15. However, it is unclear if Hog1 and Msn2/4 act independently, cooperatively, or partially cooperatively and how this interaction differs between target genes.
RESULTS
A quantitative model of the Hog1-Msn2/4 Network
To examine the interaction between Hog1 and Msn2/4 in detail, we used the mutant cycle approach (Fig. 2a) to determine the value of the three expression components in the system: H, M and Co. Expression was examined after 20 min of stress treatment (0.4 M KCl) since this is near the peak of the transient response10 but is early enough to avoid monitoring secondary effects in the mutant strains (Hog1 and Msn2/4 are inactive in prestress conditions; Table S1). We find that the influence and interaction of Hog1 and Msn2/4 varies dramatically from gene to gene (Fig. 2b); we observe a total of eight distinct regulatory modes based on the combination of statistically significant expression components at genes induced in osmotic stress (Fig. 2c). From these data it is clear that: (i) Hog1 and Msn2/4 interact, since 190 of the 273 genes in the network have a statistically significant Co component (Groups 1, 2, 5, 7, 8; Fig. 2c); and (ii) that both Hog1 and Msn2/4 are activated, and can act, separately since significant H and M components are found at 112 (Groups 4–8; Fig. 2c) and 64 genes (Groups 2, 3, 6–8; Fig. 2c), respectively.
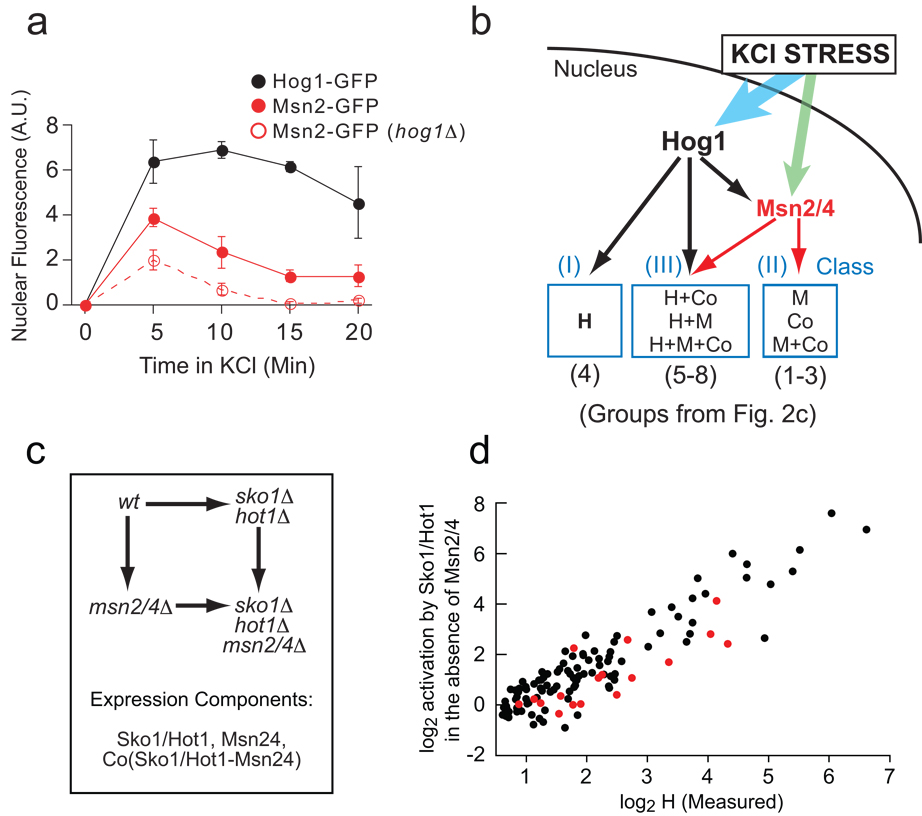
It is not possible to translate these data directly into a mechanistic network wiring diagram since the cooperative interaction between Hog1 and Msn2/4 could be established at either the promoter (Hog1 and Msn2/4 interacting on the promoter) or signaling level (Msn2/4 activity being regulated by Hog1) (Cooperative Mechanism, Fig. 1a). We surmised that the interaction between Hog1 and Msn2/4 is likely to be established, at least in part, at the signaling level, since Hog1 is a protein kinase and is required for full expression of almost all Msn2/4-dependent genes (190/203; Groups 1, 2, 5–7; Fig. 2c). Therefore, to test for activation of Msn2/4 by Hog1, we monitored the stress-induced import of Msn2/4 into the nucleus in wild-type and hog1Δ mutant strains containing GFP-tagged Msn2 or Msn4 and a nuclear marker. We observe that Hog1 is activated in KCl stress (black points, Fig. 3a) and that it contributes to activation of Msn2/4 (compare nuclear Msn2 levels in the wt and hog1Δ strains, Fig. 3a). However, Msn2/4 must also be activated by another pathway since some Msn2 is imported into the nucleus (in response to stress) even in the absence of Hog1 (Fig. 3a, Msn2-GFP in hog1Δ).
Fig. 3.
Mechanism of Hog1-dependent gene activation. (A) Hog1 promotes the nuclear import of Msn2/4 in hyper-osmotic stress. Fluorescence microscopy was used to measure the relative nuclear concentration of Hog1-GFP or Msn2-GFP, in live cells, after exposure to 0.4 M KCl. Each time-point shows the average and standard deviation from three replicate experiments, each involving 100 or more cells (Table S4). (B) Model of the Hog1 transcriptional network, explaining the expression component data found in Fig. 2 (see text for details). (C) Schema describing the experiments and equations used to break the influence of Sko1, Hot1 and Msn2/4 into components (as in Fig. 2a). (D) Correlation between the level of induction measured for Hog1 alone (H component, Fig. 2) and that from Sko1/ Hot1 in the absence of Msn2/4 (Sko1/Hot1 component, cycle part Fig. 3c) plus Sko1 repression in YEPD data (Table S1 and Supplement).
Given these connections at the signaling level, the data from the Hog1-Msn2/4 mutant cycle (Fig. 2c) can be explained by a simple wiring diagram (Fig. 3b) in which the Co component is assigned to Hog1-dependent gene activation through Msn2/4 while the H and M components are due to direct activation by Hog1 and Msn2/4, respectively. Hog1 could activate Msn2/4 through phosphorylation at one or more of 10/11 MAPK consensus sites found in these proteins, or indirectly through the other kinases, phosphatases and 14-3-3 proteins that regulate Msn2/4 nuclear import and export16–18.
Our Hog1-Msn2/4 network model defines only three classes of genes (Fig. 3b): (I) genes regulated by Hog1 alone; (II) genes regulated primarily by Hog1 through Msn2/4 (3 genes by Msn2/4 only); and (III) genes regulated by Hog1 both through Msn2/4 and independently of Msn2/4 (mixed regulation). However, the genes in Classes II (Groups 1–3) and III (Groups 5–8) show distinct behavior in deletion mutants, resulting in several groups in the expression component analysis (Fig. 2c). This can be explained if different groups of genes within a given class have different thresholds for gene activation by Msn2/4: high, low or intermediate. For example, genes in Groups 1 (Co) and 5 (H+Co) appear to have a high threshold for activation by Msn2/4 as they are insensitive to the low levels of nuclear Msn2/4 found in the absence of Hog1 (Fig. 2c; no M component). In contrast, genes in Groups 3 (M) and 6 (H+M) appear to have a low threshold for activation by Msn2/4 as they are fully activated at the low levels of nuclear Msn2/4 found in the absence of Hog1 (Fig. 2c; M but no Co component). Finally, genes in Groups 2 (M+Co) and 7 (H+M+Co) appear to have an intermediate threshold for activation as they are partially activated at the low nuclear level of Msn2/4 (Fig. 2c; M and Co component) (see Supplement for explanation of all groups).
Incorporation of Sko1 and Hot1 into the Network Model
To explain how Hog1 activates genes independently of Msn2/4 (112 genes with an H component, Groups I and III Fig. 3b) we used microarray analysis to test the role of all five TFs known or suspected to be activated by Hog1 (Sko1, Hot1, Msn1, Smp1 and Cin519–22). To our surprise, we find that only two TFs, Sko1 and Hot1, have a significant effect on osmotic stress dependent gene expression (Table S1), and that Sko1 activates many more genes (40 at >2-fold induction) than previously23,24 appreciated (Fig. S4).
To incorporate these factors into the network model we used the mutant cycle approach to dissect the influence of, and interaction between, Sko1/Hot1 and Msn2/4 (Fig. 3c). We find a striking correlation between the Sko1/Hot1 component determined in this analysis and the H component determined in the Hog1-Msn2/4 mutant cycle analysis (R=0.90, Fig. 3d). Therefore, Msn2/4-independent gene induction by Hog1 occurs almost entirely through Sko1 and Hot1. In fact, by measuring the influence that Hog1 has on gene expression in the absence of Sko1, Hot1 and Msn2/4 (on a single array, Table S1), we find that Sko1, Hot1 and Msn2/4 are required for 88% of Hog1-dependent gene activation (calculated by comparing the sum of the fold induction by Hog1 in the absence of Sko1, Hot1 and Msn2/4 to that in the wild-type strain). Only 17 of the 273 genes regulated by the HOG pathway (red points, Fig. 3d) are activated >1.5-fold (p<0.05) by additional (unknown) Hog1-dependent TFs.
By analyzing the cooperative component from the Sko1/Hot1-Msn2/4 mutant cycle (Fig. 3c) we were also able to define the logic gates at individual promoters. We find that there are very few positively cooperative (AND) interactions between Sko1/Hot1 and Msn2/4 (i.e. few genes with a statistically significant positive cooperative component; 5 observed versus 2 false positives expected, at p<0.01, and 9 versus 9 at p<0.05), validating our assertion that positive Hog1-Msn2/4 cooperativity is established at the signaling level (i.e. Hog1 regulating Msn2/4 activity; Fig. 3b). Instead, we find that Sko1/Hot1 and Msn2/4 act redundantly (negative Co component, OR interactions) or through SUM gate logic (no Co component; the output is the log sum of the individual components) at the promoter level (see Supplement).
To complete our model, we dissected the influence of Sko1/Hot1 into individual expression components using two further mutant cycles (see Supplement and Table S2) and identified the Sko1 and Hot1 target genes using chromatin immunoprecipitation followed by microarray hybridization (ChIP-chip) analysis (Fig. 4a). These data revealed that 65–80% of the genes repressed by Sko1 (27 total), activated by Sko1 (52 total), or activated by Hot1 (15 total) are bound by the appropriate factor in the appropriate condition at p<0.05 (Fig. 4b and Supplement); these findings are further supported by our detailed analysis of regulatory motifs where we find that Sko1, Hot1 and Msn2/4 binding sites are highly enriched in the appropriate gene-sets (see Supplement). Finally, we find that over half of the Sko1 and Hot1 target sites identified through ChIP analysis are silent (<1.5-fold activation), and thus non-functional, in the conditions studied here (Fig. 4c, d and Supplement). These results highlight both the accuracy of our mutant cycle approach and the limitations of using ChIP-chip (alone) for identifying functional interactions within transcriptional networks.
Fig. 4.
ChIP analysis of Sko1 and Hot1 binding sites (A) Sample raw data for Sko1 (upper panel) and Hot1 (lower panel) for a region of chromosome 8 (approximately 1% of the genome). Each data point shows the Cy5/Cy3 ratio for one probe on the array. The inset shows an example of a fit of the data to the peak shape model used to analyze the data (see Methods and Supplement). The solid line shows the best-fit prediction of the binding site position, while the dotted lines show the 99% confidence interval. The ChIP data is listed in Tables S2 and S3. (B) Overlap of ChIP and expression data. The target genes shown in Fig. S5c for Sko1, Hot1 and Msn2/4 alone (p<0.05) were compared to the target genes identified in the ChIP analysis from the peak fitting (p<0.05). In the case of Sko1 (+KCl) the p-value was relaxed to 0.058 since we found significantly better coverage at this value. This is likely due to a lower binding affinity of Sko1 to genes that are only bound in stress conditions (and thus a lower peak height/significance). (C) Venn diagram showing the overlap between ChIP data (p<0.05) and expression data (p<0.058) for Sko1. The number of binding sites at genes without significant Sko1 induction and/or repression, is adjusted for the expected number of false positives. The bar graphs show the number of genes that are repressed (R), repressed and activated (R+A) or just activated, for genes where there is both significant binding and expression data. (D) Venn diagram showing the overlap between ChIP data (p<0.05) and expression data (p<0.05) for Hot1. Again here the number of binding sites at genes without significant Hot1 induction is corrected for the number of false positives expected.
Signal Integration in the Hog1 Network
Taken together, our data provide a detailed model of the Hog1 transcriptional network in KCl-induced osmotic stress (Fig. 5). Examination of this network reveals that the signals sent through Hog1 and the general stress (Msn2/4) pathways are integrated at two levels. At the signaling level, Hog1 and at least one additional pathway function together to activate Msn2/4 and trigger its nuclear import (Fig. 3b). At the promoter level, the signal transmitted through Hog1, via Sko1 and Hot1, combines with Msn2/4 at a subset of the general stress response genes (Fig. 5). Therefore, the Hog1-Msn2/4 transcriptional network appears to have evolved to create an osmotic stress response that is modulated by signals that regulate Msn2/4 (which could include the PKA, TOR, Snf1 and other pathways16–18,25).
Fig. 5.
Structure of the transcriptional network activated by the MAPK Hog1. Genes are grouped based on common regulatory mechanisms (denoted by a box with the names of two sample genes) and only shown if two or more genes have the same connections as determined by expression and confirmed by ChIP. Broken lines indicate interactions that that exist for only part of a group. The number in each box refers to the number of genes in a group based on expression data alone. To simplify the figure silent binding events are not shown and there is no representation of cooperativity at the promoter level. All of the values describing the network are listed in Table S2.
To test this prediction, we examined the Hog1-Msn2/4 network in an additional stress condition: hyper-osmotic stress caused by high glucose concentrations. Glucose is known to reduce Msn2/4 activity16,25 and is biologically relevant, as high glucose levels (including levels similar to those tested here) are encountered by yeast when they grow on fruit26. To simplify our analysis, the level of osmotic stress (total molar osmolarity) used in the glucose and KCl experiments was identical. Since the HOG pathway senses the level of osmotic stress (turgor pressure27), we expected that Hog1 would be activated to a similar level in both KCl and glucose, but that Msn2/4 activation would be different in these two conditions.
We find that the HOG pathway activates fewer genes in glucose than in KCl (187 vs 367 at >1.5-fold). To identify the basis of this change, we applied the mutant cycle approach (Fig. 2a) to determine the value of the three expression components (H, M and Co) in glucose and compared the data to that from KCl stress for each gene (Figs. 6a–c). In agreement with our initial predictions, we find that in the absence of Msn2/4, Hog1 has a similar impact on gene expression in glucose and KCl stress (H component, Fig. 6a). By contrast, Msn2/4-dependent gene activation (M+Co components) is substantially decreased in glucose (Fig. 6b) and this decrease extends to Hog1-Msn2/4 dependent gene induction (Co component, Fig. 6c). In accord with these results, activation of Msn2/4 (monitored by nuclear localization) is decreased in glucose compared to KCl stress, while activation of Hog1 is identical in the two stress conditions (Fig. 6d). Thus, the osmotic stress response in high glucose is modulated, when compared to that in high salt, by inhibition of Msn2/4 activity (Fig. 6e, left vs. right panels). This leads to an overall decrease in the activation of the general stress response, and shifts the Hog1-dependent expression program towards genes regulated by Sko1 and Hot1.
Fig. 6.
Context-dependent gene activation by the Hog1-Msn2/4 network. (A) Plot comparing the H component in KCl stress (0.4 M) and glucose stress (0.8 M). Each point shows the data for a single gene; colored red if (HGlu-HKCl)<1.5, p<0.05; green if (HKCl-HGlu)<1.5, p<0.05); and black if there is no significant change. The solid and broken lines show the values expected for perfect correlation and a ±1.5-fold difference, respectively. Data is shown for all genes with a significant H component (H<1.5-fold, p<0.01) in KCl or glucose (n=170). (B) Plot comparing the total influence of Msn2/4 (M component + Co component), in osmotic stress due to 0.4 M KCl (X-axis) or 0.8 M glucose (Y-axis). Gene selection (M+Co<1.5-fold, p<0.01; n=280) and lines are as in (A). (C) Plot comparing the cooperative influence of Hog1 and Msn2/4 (Co component) on gene expression, in osmotic stress due to 0.4 M KCl or 0.8 M glucose. The lines are as in (C) and the genes are those shown in (B). (D) Time-course of Hog1 and Msn2 nuclear import during KCl and glucose stress (as described for Fig. 3a). (E) Model of the Hog1-Msn2/4 network in KCl (left panel) and high glucose (right panel).
Discussion
Previous analysis of the Hog1 dependent stress response led to a coarse-grained model of Hog1 function where the kinase regulates gene expression through three entirely independent paths: activation of Msn2/4; activation of Hot1; and de-repression of Sko1, with Sko1 and Hot1 acting at only 12 genes15,28. Since the transcription factors Msn2/4 are activated in diverse stress conditions and regulate >100 genes, this model led to the view that the osmotic stress response is largely nonspecific29. This network structure, and previous data comparing the gene expression program in salt and sorbitol, also suggested that the Hog1 dependent transcriptional response is the same in all osmolytes10.
Using the mutant cycle approach, we have converted the previously incomplete and qualitative description of Hog1 dependent gene activation into a quantitative and nearly complete network model (Fig. 5 and values in Table S3). Our model shows that the signal from Hog1 is spread out to multiple transcription factors and then recombined in different ways at different promoters (Fig. 5). This network architecture allows stress signals transmitted through Hog1 to not only influence the general stress program via Msn2/4 but to supplement and tune it as well (Fig. 5 and 6e). The osmotic stress response is therefore highly specific as Hog1 acts at least partially independently of Msn2/4 at many genes (112 in total; Fig. 2). It is likely that these genes – which are involved in a wide-range of processes including glycerol synthesis, free radical breakdown, ion transport, general metabolism and signaling (Table S2) – play a central role in adapting to osmotic stress. In addition, we find that in KCl stress, signals are transmitted through both the Hog1 and general stress (Msn2/4) pathways and then integrated at the signaling and promoter level (Fig. 6). By comparing the transcriptional response in glucose to that in KCl we show that this network architecture allows budding yeast to respond to different osmolytes in different ways (as described in detail below); that is, the transcriptional program activated by Hog1 is context dependent.
What is the functional significance of the Hog1 network structure and the signal integration we have uncovered? A recent study of Hog1 signaling dynamics demonstrates that the Hog1 dependent transcriptional response in high salt stress functions to prepare cells for future changes in osmolarity while the immediate response to osmotic stress depends on more rapid post-translational mechanisms30. We find that this transcriptional response includes the 200-gene general stress response (through Msn2/4) as well as 70 additional genes activated by Hog1 alone (through Sko1/Hot1 and at least one unknown factor; Fig. 3d). This broad program likely prepares the cell for both the damage caused by salt (due to disruption of protein-protein and protein-DNA interactions31) and the osmotic imbalance induced in these harsh conditions. By contrast, when the osmotic stress is created by glucose, cells activate the 70 genes controlled by Hog1 alone, but do not expend the energy needed to activate the full 200 gene general (Msn2/4 dependent) stress program. This makes sense, as cell damage is likely to be limited under such conditions and Msn2/4 activation leads to energy conservation and slow growth32, a process that is likely to be disadvantageous in a high glucose environment such as fruit. Instead, only a subset of the Msn2/4 dependent genes are activated in high glucose – those where Sko1/Hot1 and Msn2/4 cooperate to induce expression (Fig. 6). Interestingly, these genes are regulated in two distinct ways by the Hog1 network. At genes where Sko1/Hot1 and Msn2/4 cooperate with SUM gate logic, the expression levels are boosted above that created by the general stress response (Msn2/4) whenever Hog1 is activated. This form of regulation is found at several genes involved in converting glucose into the osmolyte glycerol (HXT1, YGR043C, DAK1 and TKL2), suggesting that additional capacity (beyond that created by Msn2/4 alone) through this pathway is beneficial in all osmotic stress conditions. By contrast, Sko1/Hot1 activity only alters expression at genes with OR gate logic when Msn2/4 activity is low (e.g. in high glucose). The genes regulated in this manner play more generic roles in stress recovery such as neutralizing free radicals and cell wall/cell membrane repair (e.g. CTT1, HSP12, SPI1 and YNL194c) and appear to be required at some minimum level after osmotic stress.
Overall, our model of the Hog1 network provides insight into the way a signal can create a context dependent gene expression program using a limited number of transcription factors. Because Hog1 acts through the general stress regulators Msn2/4, the response to osmotic stress depends on the combined action of multiple pathways (those regulating Msn2/4) and thus the overall state of the cell. However, by acting in parallel through the osmotic stress specific transcription factors Sko1 and Hot1, this generic stress response is adapted so that it is specific to, and presumably appropriate for, osmotic stress in at least two different stress conditions. We therefore anticipate that other stress signals will be transmitted through networks with a similar overlapping structure.
Beyond establishing the structure and function of the Hog1 transcriptional network, our results demonstrate the utility of double mutant analysis, and the overall strategy taken here, for dissecting gene regulatory systems. We have shown that, starting with two or more known/putative network components, it is possible to build a quantitative genome-wide network model and to identify the genes regulated by missing components. By performing a screen for the factors that act on these genes (using bioinformatics, microarrays, or reporter strains), it is possible to identify the missing components and integrate them into the network model. This approach has immediate application to studying conditionally activated pathways (and drug-pathway interactions) using gene KOs, and can be extended to other systems through the use of RNAi and chemical inhibitors.
Methods
S. cerevisiae Strains
The strains examined in this study were constructed in a W303 background, as described in the supplement, and are listed in Table S5.
Expression Microarrays
An overnight culture of yeast was used to inoculate a 1 L culture to an OD600 of 0.05 in a 2 L conical flask shaking at 200 rpm at 30 °C. These cells were grown to an OD600 between 0.55–0.60 and then 250 ml of cells were collected by filtration and frozen in liquid nitrogen. At this time 500 ml of YEPD containing 0.9375 M KCl (at 30 °C) was added to the culture, and then the cells were harvested (after 20min), again using filtration, and frozen. In each case, strains that were compared on a single two-color microarray were grown in parallel in the same batch of medium and treated with identical YEPD + KCl. RNA was then purified from the frozen cells, converted into cDNA using reverse transcription, labeled with Cy3 or Cy5 and examined using Agilent G4140A microarrays (see supplement for details).
Microscopy
Strains expressing a GFP-tagged protein and RFP-tagged Nhp6a (a nuclear marker), were grown in SD medium to an OD600 of 0.1 at 30 °C. These tubes were then transferred to a roller-drum in the microscope room (23 °C) for approx 1 hr. 50 µl of cells were then added to a well of a 96 well glass bottomed plate and allowed to settle for 5–10 min. At this time 30 µl of 1.0 M KCl in SD medium (or SD medium alone for the background control) were added to the cells and DIC and fluorescence images (in the eGFP and RFP channels) were collected in five separate fields using a Zeiss Axiovert inverted microscope fitted with a Cascade 512B camera and an oil-immersion Zeiss 63x achromatic objective. The nuclear fluorescence of each cell was then determined in both the GFP and RFP channels using Metamorph (version 7). The nuclear region was identified using the signal in the RFP channel and overlaid onto the GFP image. The nuclear fluorescence within these regions was then calculated for each cell, and averaged. Data was only recorded for cells that were free from overlap in the DIC image and had their nuclei in the focal plane (based on a cutoff for low RFP signal intensity), usually 100–200 cells per time point. The values reported are the average and standard deviation from three separate experiments. Sample images are shown in Table S4.
Chromatin immunoprecipitation and read out on microarrays (ChIP-chip)
Cells with HA-tagged Sko1 or TAP-tagged Hot1 were grown to OD600 of 0.6 in YEPD as described for the expression arrays, and then treated with YEPD + KCl (to 0.375 M final) or YEPD alone. Five minutes after the application of stress, cells were treated with 1% formaldehyde for 15 min at room temperature. Cross-linking was then stopped by the addition of 125 mM glycine to the culture and the cells were washed twice with PBS at 4 °C and harvested by centrifugation. Cells were lysed by bead beating as described in (33) and the chromatin sheared using a Missonex 3000 sonicator fitted with a microtip (5 × 15 sec, power setting 1.5). This led to an average fragment size of 500–1000 bp. The DNA crosslinked to the TF was then immunopreciptated using 12CA5 and protein G Fastflow Sephadex (Pharmacia) for Sko1-HA, or IgG magnetic beads (Dynal) for Hot1-TAP, and purified as described in (33). These samples were then amplified, in parallel with the original sonicated DNA from the same strains (as a genomic control), using random priming PCR34 with amino allyl-UTP in the mix, as described in (35). Immunoprecipitated samples were then labeled with Cy5, and genomic DNA labeled with Cy3, as described for the expression arrays. 2 µg of a Cy5-labeled sample and 2 µg of the appropriate Cy3-labeled genomic control were then hybridized to a custom Agilent microarray with 44,000 60bp probes (see supplement for a description). These arrays were then washed and scanned using the procedure described for the expression arrays. Similar procedures were also carried out for Msn2 (tagged with HA or TAP), but here we were unable to detect significant binding by real-time PCR even at well-established target genes (including CTT1 and HSP12). Inspection of previous ChIP data for Msn2 and Msn4 reveals that only a small subset of the known target genes for these factors are enriched by ChIP4, suggesting that the problems arise from a property of the TFs themselves.
Expression Component Analysis
As described in detail in the supplement, the system of equations listed in Fig. 2a can be formulated as the following matrix multiplication:
or Y = X * β + ε, where Y are the measured values from each microarray, X is the design matrix, β is the contribution of the three expression components, and ε is the noise. For each gene, we wish to find a β which minimizes the errors, ε.
To solve this linear model, we applied a multiple linear regression algorithm which minimizes the least squares fit of X*β, assuming a zero-mean Normal distribution of the errors ε. Specifically, the equation above X * β = Y is multiplied (from the left) by XT, to get: XT * X * β = XT * Y. In our case, the matrix XT *X is non-singular, and so we invert XT *X and use it to multiply the equation (from left), and obtain a unique solution for the vector of regression coefficient β = (XT * X)−1 * XT * Y.
It is assumed that all the coefficients in β have a zero-centered normal distribution, and so we can estimate their variance and covariance values. Specifically, Cov(β) = σ2 * (XT * X)−1, where σ2 is the variance of the fit. As described in the supplement, these properties pave the way for testing hypotheses about the estimated values of regression coefficients β. A similar approach was used to analyze the other mutant cycles in this study (see supplement).
Supplementary Material
Acknowledgments
We thank Dave Steger, Dennis Wykoff, Adam Carroll, and Chris Hopkins from Agilent for advice regarding microarray, ChIP and other procedures; Tony Lee and Rick Young for sharing their tilling array design and hybridization protocol prior to publication; Hanah Margalit and members of the O’Shea, Friedman and Regev labs for helpful discussions; and Paul Grosu for help with Rosetta Resolver. We are also grateful to Eric Lander, Dana Pe’er, Daphne Koller, Rich Losick, Michael Brenner and Bodo Stern for reading the manuscript prior to publication. APC was a Howard Hughes Medical Institute (HHMI) Fellow of the Life Sciences Research Foundation. This work was supported by HHMI (EKO) and a grant from the Human Frontiers Science Program.
Footnotes
ChIP Analysis
ChIP on chip analysis was preformed using a custom peak-fitting algorithm described in the supplement and http://compbio.cs.huji.ac.il/HOG/.
URLs
The supplementary datasets and figures are available at http://compbio.cs.huji.ac.il/HOG/
Accession Codes
The microarray data for this study have been deposited in the GEO database and have accession number GSE 12270.
References
- 1.Alon U. An introduction to systems biology : design principles of biological circuits. Boca Raton, FL: Chapman & Hall/CRC; 2007. [Google Scholar]
- 2.Davidson EH. The regulatory genome : gene regulatory networks in development and evolution. Burlington, MA: Academic; 2006. [Google Scholar]
- 3.Boyer LA, et al. Core transcriptional regulatory circuitry in human embryonic stem cells. Cell. 2005;122:947–956. doi: 10.1016/j.cell.2005.08.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Harbison CT, et al. Transcriptional regulatory code of a eukaryotic genome. Nature. 2004;431:99–104. doi: 10.1038/nature02800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hu Z, Killion PJ, Iyer VR. Genetic reconstruction of a functional transcriptional regulatory network. Nat Genet. 2007;39:683–687. doi: 10.1038/ng2012. [DOI] [PubMed] [Google Scholar]
- 6.Hughes TR, et al. Functional discovery via a compendium of expression profiles. Cell. 2000;102:109–126. doi: 10.1016/s0092-8674(00)00015-5. [DOI] [PubMed] [Google Scholar]
- 7.Avery L, Wasserman S. Ordering gene function: the interpretation of epistasis in regulatory hierarchies. Trends Genet. 1992;8:312–316. doi: 10.1016/0168-9525(92)90263-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lee TI, et al. Redundant roles for the TFIID and SAGA complexes in global transcription. Nature. 2000;405:701–704. doi: 10.1038/35015104. [DOI] [PubMed] [Google Scholar]
- 9.Van Driessche N, et al. Epistasis analysis with global transcriptional phenotypes. Nat Genet. 2005;37:471–477. doi: 10.1038/ng1545. [DOI] [PubMed] [Google Scholar]
- 10.O'Rourke SM, Herskowitz I. Unique and redundant roles for HOG MAPK pathway components as revealed by whole-genome expression analysis. Mol Biol Cell. 2004;15:532–542. doi: 10.1091/mbc.E03-07-0521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Roberts CJ, et al. Signaling and circuitry of multiple MAPK pathways revealed by a matrix of global gene expression profiles. Science. 2000;287:873–880. doi: 10.1126/science.287.5454.873. [DOI] [PubMed] [Google Scholar]
- 12.Eichenberger P, et al. The program of gene transcription for a single differentiating cell type during sporulation in Bacillus subtilis. PLoS Biol. 2004;2:e328. doi: 10.1371/journal.pbio.0020328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Horovitz A, Fersht AR. Co-operative interactions during protein folding. J Mol Biol. 1992;224:733–740. doi: 10.1016/0022-2836(92)90557-z. [DOI] [PubMed] [Google Scholar]
- 14.Reiser V, Ruis H, Ammerer G. Kinase activity-dependent nuclear export opposes stress-induced nuclear accumulation and retention of Hog1 mitogen-activated protein kinase in the budding yeast Saccharomyces cerevisiae. Mol Biol Cell. 1999;10:1147–1161. doi: 10.1091/mbc.10.4.1147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rep M, Krantz M, Thevelein JM, Hohmann S. The transcriptional response of Saccharomyces cerevisiae to osmotic shock. Hot1p and Msn2p/Msn4p are required for the induction of subsets of high osmolarity glycerol pathway-dependent genes. J Biol Chem. 2000;275:8290–8300. doi: 10.1074/jbc.275.12.8290. [DOI] [PubMed] [Google Scholar]
- 16.Garreau H, et al. Hyperphosphorylation of Msn2p and Msn4p in response to heat shock and the diauxic shift is inhibited by cAMP in Saccharomyces cerevisiae. Microbiology. 2000;146(Pt 9):2113–2120. doi: 10.1099/00221287-146-9-2113. [DOI] [PubMed] [Google Scholar]
- 17.De Wever V, Reiter W, Ballarini A, Ammerer G, Brocard C. A dual role for PP1 in shaping the Msn2-dependent transcriptional response to glucose starvation. Embo J. 2005;24:4115–4123. doi: 10.1038/sj.emboj.7600871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Beck T, Hall MN. The TOR signalling pathway controls nuclear localization of nutrient-regulated transcription factors. Nature. 1999;402:689–692. doi: 10.1038/45287. [DOI] [PubMed] [Google Scholar]
- 19.de Nadal E, Casadome L, Posas F. Targeting the MEF2-like transcription factor Smp1 by the stress-activated Hog1 mitogen-activated protein kinase. Mol Cell Biol. 2003;23:229–237. doi: 10.1128/MCB.23.1.229-237.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nevitt T, Pereira J, Azevedo D, Guerreiro P, Rodrigues-Pousada C. Expression of YAP4 in Saccharomyces cerevisiae under osmotic stress. Biochem J. 2004;379:367–374. doi: 10.1042/BJ20031127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Proft M, Serrano R. Repressors and upstream repressing sequences of the stress-regulated ENA1 gene in Saccharomyces cerevisiae: bZIP protein Sko1p confers HOG-dependent osmotic regulation. Mol Cell Biol. 1999;19:537–546. doi: 10.1128/mcb.19.1.537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Rep M, et al. Osmotic stress-induced gene expression in Saccharomyces cerevisiae requires Msn1p and the novel nuclear factor Hot1p. Mol Cell Biol. 1999;19:5474–5485. doi: 10.1128/mcb.19.8.5474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rep M, et al. The Saccharomyces cerevisiae Sko1p transcription factor mediates HOG pathway-dependent osmotic regulation of a set of genes encoding enzymes implicated in protection from oxidative damage. Mol Microbiol. 2001;40:1067–1083. doi: 10.1046/j.1365-2958.2001.02384.x. [DOI] [PubMed] [Google Scholar]
- 24.Proft M, Gibbons FD, Copeland M, Roth FP, Struhl K. Genomewide identification of Sko1 target promoters reveals a regulatory network that operates in response to osmotic stress in Saccharomyces cerevisiae. Eukaryot Cell. 2005;4:1343–1352. doi: 10.1128/EC.4.8.1343-1352.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gorner W, et al. Nuclear localization of the C2H2 zinc finger protein Msn2p is regulated by stress and protein kinase A activity. Genes Dev. 1998;12:586–597. doi: 10.1101/gad.12.4.586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Erasmus DJ, van der Merwe GK, van Vuuren HJ. Genome-wide expression analyses: Metabolic adaptation of Saccharomyces cerevisiae to high sugar stress. FEMS Yeast Res. 2003;3:375–399. doi: 10.1016/S1567-1356(02)00203-9. [DOI] [PubMed] [Google Scholar]
- 27.Reiser V, Raitt DC, Saito H. Yeast osmosensor Sln1 and plant cytokinin receptor Cre1 respond to changes in turgor pressure. J Cell Biol. 2003;161:1035–1040. doi: 10.1083/jcb.200301099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hohmann S, Krantz M, Nordlander B. Yeast osmoregulation. Methods Enzymol. 2007;428:29–45. doi: 10.1016/S0076-6879(07)28002-4. [DOI] [PubMed] [Google Scholar]
- 29.Gasch AP, et al. Genomic expression programs in the response of yeast cells to environmental changes. Mol Biol Cell. 2000;11:4241–4257. doi: 10.1091/mbc.11.12.4241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mettetal JT, Muzzey D, Gomez-Uribe C, van Oudenaarden A. The frequency dependence of osmo-adaptation in Saccharomyces cerevisiae. Science. 2008;319:482–484. doi: 10.1126/science.1151582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Proft M, Struhl K. MAP kinase-mediated stress relief that precedes and regulates the timing of transcriptional induction. Cell. 2004;118:351–361. doi: 10.1016/j.cell.2004.07.016. [DOI] [PubMed] [Google Scholar]
- 32.Durchschlag E, Reiter W, Ammerer G, Schuller C. Nuclear localization destabilizes the stress-regulated transcription factor Msn2. J Biol Chem. 2004;279:55425–55432. doi: 10.1074/jbc.M407264200. [DOI] [PubMed] [Google Scholar]
- 33.Robyr D, Kurdistani SK, Grunstein M. Analysis of genome-wide histone acetylation state and enzyme binding using DNA microarrays. Methods Enzymol. 2004;376:289–304. doi: 10.1016/S0076-6879(03)76019-4. [DOI] [PubMed] [Google Scholar]
- 34.Bohlander SK, Espinosa R, 3rd, Le Beau MM, Rowley JD, Diaz MO. A method for the rapid sequence-independent amplification of microdissected chromosomal material. Genomics. 1992;13:1322–1324. doi: 10.1016/0888-7543(92)90057-y. [DOI] [PubMed] [Google Scholar]
- 35.Iyer VR, et al. Genomic binding sites of the yeast cell-cycle transcription factors SBF and MBF. Nature. 2001;409:533–538. doi: 10.1038/35054095. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.