Abstract
Motivation: Ontologies are essential in biomedical research due to their ability to semantically integrate content from different scientific databases and resources. Their application improves capabilities for querying and mining biological knowledge. An increasing number of ontologies is being developed for this purpose, and considerable effort is invested into formally defining them in order to represent their semantics explicitly. However, current biomedical ontologies do not facilitate data integration and interoperability yet, since reasoning over these ontologies is very complex and cannot be performed efficiently or is even impossible. We propose the use of less expressive subsets of ontology representation languages to enable efficient reasoning and achieve the goal of genuine interoperability between ontologies.
Results: We present and evaluate EL Vira, a framework that transforms OWL ontologies into the OWL EL subset, thereby enabling the use of tractable reasoning. We illustrate which OWL constructs and inferences are kept and lost following the conversion and demonstrate the performance gain of reasoning indicated by the significant reduction of processing time. We applied EL Vira to the open biomedical ontologies and provide a repository of ontologies resulting from this conversion. EL Vira creates a common layer of ontological interoperability that, for the first time, enables the creation of software solutions that can employ biomedical ontologies to perform inferences and answer complex queries to support scientific analyses.
Availability and implementation: The EL Vira software is available from http://el-vira.googlecode.com and converted OBO ontologies and their mappings are available from http://bioonto.gen.cam.ac.uk/el-ont.
Contact: rh497@cam.ac.uk
1 INTRODUCTION
The amount and complexity of data in the life sciences has instigated the development of a large number of biological databases. However, our ability to discover knowledge across these heterogeneous data is impaired without a common framework to semantically annotate the data so as to facilitate the archival, retrieval, integration and analysis of multiply authored knowledge. In the past decade, ontologies have filled the gap of being able to explicitly specify the meaning of terms in a vocabulary (Gruber, 1993; Guarino, 1998). With over 200 ontologies listed in the BioPortal (Noy et al., 2009), specifying the meaning of more than 1.4 million terms, ontologies have become an important component in the integration of biomedical data. Although many biomedical ontologies are made available using the OBO Flatfile Format (Horrocks, 2007), they are increasingly being represented in more expressive formal languages, in particular the Web Ontology Language (OWL) (Grau et al., 2008) or they can be converted to OWL (Hoehndorf et al., 2010c). OWL ontologies can be used with automated reasoners to determine whether the ontology contains contradictory assertions, whether classes in the ontology are satisfiable (i.e. is it logically possible for a class to have instances?) or for subsumption checking (i.e. is a class C a subclass of a class D?).
Most major biomedical databases employ one or more of these ontologies. Yet, to successfully apply ontologies to data integration and interoperability, it is necessary to integrate the ontologies in a common model, for example by formally relating their terms to the terms in other ontologies. This problem is now being addressed as terms in biomedical ontologies are increasingly being defined using terms from multiple, often domain-independent, ontologies (Gkoutos et al., 2004; Mungall et al., 2010a, b, c). For example, the phenotype Abnormal bile secretion [from Human or Mammalian Phenotype Ontology (Robinson et al., 2008; Smith et al., 2004)] can be defined as a Secretion [from Gene Ontology (Ashburner et al., 2000)] that has Hepatocyte [from Celltype Ontology (Bard et al., 2005)] as agent, occurs in the Liver [from Foundational Model of Anatomy (FMA) (Rosse and Mejino, 2003) or Mouse Anatomy Ontology (Hayamizu et al., 2005)] and results in a movement of Bile (from FMA or Mouse Anatomy Ontology) into the Bile canaliculus (from FMA or Mouse Anatomy Ontology). Data annotated to the phenotype Abnormal bile secretion can be formally related to data annotated with the biological process Secretion or the anatomical structures Bile canaliculus and Liver, as well as to the secreted product Bile and the cell type Hepatocyte involved in the secretory process. This permits the ontology-based discovery of relations between data that are not made explicit at the time of annotation. In this example, the anatomical location Bile canaliculus is not asserted in the term, but is used in the term's definition. Therefore, it would be possible to automatically search databases for processes which are anatomically co-localized with bile secretion, provided that the data in multiple databases are available in a shared model and that multiple formally defined ontologies are exploitable through automatic reasoning.
While the use of OWL offers many advantages, and significant advancements were made to develop efficient and highly optimized algorithms for reasoning, the established theoretical lower bounds for inference over OWL means that tractable (i.e. guaranteed polynomial time) algorithms will never be available for reasoning over these ontologies. Reasoning in OWL is 2NEXPTIME-hard (Tobies, 2000), and therefore the time required to decide relevant problems in OWL increases, in the worst case, doubly exponentially (22x) with the number of logical operators used in an ontology. Although this complexity is rarely reached in ontologies currently used within the biomedical domain (Horrocks et al., 2000; Motik et al., 2009a; Rector and Brandt, 2008), several large biomedical ontologies cannot yet be utilized for automated reasoning in OWL, in particular when an ontology's classes are richly defined (Golbreich et al., 2006; Mungall et al., 2010a, c).
As a consequence, current ontology-based resources such as the various model organism databases, search engines, ontology repositories, ontology browsers and interfaces, make little or no use of the semantic power of the ontologies at all. Instead, unique, case-based interpretations are assigned to the entities found in ontologies, and documented in software code and database schemata. Unless an ontology's semantics can be employed by ontology-based applications and methods, the original goal of ontologies to facilitate data integration and interoperability cannot be achieved, thereby diminishing the value of the ontology development and maintenance efforts of the past decade.
In the most recent version of OWL (OWL2), three profiles (syntactic and semantic subsets) were developed: OWL EL, OWL QL and OWL RL (Motik et al., 2009b). Of interest here is that these profiles support tractable automated reasoning while sacrificing some of the OWL expressivity (Baader et al., 2006b; Motik et al., 2009b). For example, OWL EL does not support the use of class descriptions that utilize union or negation statements, and neither does it support symmetric or functional object properties. When using OWL EL, the use of ontologies for consistency verification is impaired due to the lack of negation in OWL EL. The reduction in expressivity further leads to fewer inferences that can be drawn from an ontology. For example, when inferring the taxonomic backbone of a phenotype ontology based on its formal definitions, statements involving negation play an important role in representing abnormality and absence (Hoehndorf et al., 2010b). Inferences using such definitions of abnormality and absence would not be possible in OWL EL, and consequently, the taxonomic structure of some ontologies could not be inferred.
However, once an ontology's taxonomic structure has been computed using automated reasoning in OWL, the resulting structure can be represented in OWL EL and used for automated inferences. OWL EL is particularly useful for representing and processing ontologies that contain a large number of classes, and despite the limitations that OWL EL places on OWL expressivity, OWL EL is already being applied in large-scale medical classification systems like SNOMED CT (Schulz et al., 2009a; Suntisrivaraporn, 2008). Additionally, an increasing number of automated reasoners provide support for OWL EL (http://www.w3.org/2007/OWL/wiki/Implementations).
Here, we investigate the use of EL as a common layer of formal interoperability for all biomedical ontologies. We developed EL Vira, a software package to convert ontologies into OWL EL. Using the EL Vira, software guarantees that ontologies can be converted and disseminated in the EL subset of OWL, while both maintaining compatibility with more expressive version of the ontologies and sacrificing as little of their inferences as possible. The use of such a layer of interoperability is necessary if ontologies are to achieve their goal of data integration and interoperability, not only in a static sense that is applied in database annotations but also in the more important dynamic sense that is determined by how these ontologies are used.
2 SYSTEM AND METHODS
2.1 OWL EL
The OWL EL profile is a subset of OWL that is based on the description logic EL++ (Baader et al., 2006b). In EL++, class intersections and existential quantifications, which make up a large fraction of the axioms in biomedical ontologies, can be used without limitation. EL++ further supports property chains and transitivity of object properties. It does not support the use of disjunctive class descriptions and symmetry constraints on object properties, and also restricts the use of negation and universal quantification. The supported and unsupported OWL fragments in the EL profile are specified in a W3C recommendation (Motik et al., 2009b) and listed in Table 1.
Table 1.
Allowed and disallowed OWL constructs in OWL EL (Motik et al., 2009b)
| Type of OWL construct | Allowed | Disallowed |
|---|---|---|
| Class axioms | Class inclusion | |
| Class equivalence | ||
| Class disjointness | ||
| Object property axioms | Domain restrictions | Disjoint object properties |
| Range restrictions | Irreflexive object properties | |
| Object property inclusion (with property chains) | Functional object properties | |
| Object property equivalence | Inverse-functional object properties | |
| Transitive object properties | Symmetric object properties | |
| Reflexive object properties | Asymmetric object properties | |
| Functional object properties | ||
| Inverse-functional object properties | ||
| Inverse object properties | ||
| Data property axioms | Data property inclusion | Disjoint data properties |
| Data property equivalence | ||
| Functional data properties | ||
| Class restrictions | Intersection of classes | Disjunction of classes |
| Negation of classes | ||
| Intersection of data ranges | Disjunction of data ranges | |
| Existential quantification to class expression | Universal quantification to class expression | |
| Existential quantification to data range | Universal quantification to a data range | |
| Existential quantification to an individual | ||
| Cardinality restrictions | ||
| Enumerations to a single individual | Enumerations involving more than one individual | |
| Enumerations to a single literal | Enumerations involving more than one literal | |
| Individual assertions | All types |
To achieve tractable reasoning, existential quantifications and intersections of classes are permitted. No disjunctions, negations or universal restrictions are allowed in OWL EL, as they lead to higher complexity (Baader et al., 2005).
Class satisfiability (i.e. can a class have instances?) and subsumption checking (i.e. is a class C a subclass of a class D?) is decidable in polynomial time in EL++ (Baader et al., 2005). Consequently, it can be used for the classification of and queries over much larger knowledge bases than OWL, albeit with the loss of some expressivity. Reasoning on EL++ can further be parallelized (Battista and Dumontier, 2009) and distributed using the Map-Reduce framework (Mutharaju et al., 2010), thereby providing scalability even for large ontologies. This makes EL++ useful for the implementation of ontology-based applications, in particular when large biomedical ontologies are used. Table 2 lists biomedical ontologies that are not readily available in EL++.
Table 2.
Selected OBO ontologies (and their respective OWL constructs) that are not directly available in EL
| Ontology | Expressivity |
|---|---|
| Fungal gross anatomy ontology | ALEI+ |
| Spatial ontology | ALEHI+ |
| Teleost anatomy ontology | ALERI+ |
| Dentritic cell ontology | ALC |
| Lipid ontology | ALCHIN |
| Software ontology | ALCHOIQ(D) |
| Celltype ontology | S |
| Uberon anatomy ontology | SR |
| Sequence ontology | SHI |
| Chemical information ontology | SHIQ(D) |
| Infectious disease ontology | SHOI |
| Influenza ontology | SHOIN(D) |
| Information artifact ontology | SHOIN(D) |
| Ontology of biomedical investigations | SHOIN(D) |
| Vaccine ontology | SHOIN(D) |
The letters in the expressivity column signify the used OWL constructs, and stand for: AL—language with negation of primitive classes, intersection, universal quantification, (limited) existential quantification; C—class negation; E—existential restriction; I—inverse properties; H—property inclusions; N—cardinality restrictions; Q—qualified cardinality restrictions; (D)—use of data properties; O—use of enumerations; R—reflexive, irreflexive and disjoint object properties and property chains; S—ALC with transitive object properties.
2.2 OWL EL reasoners
We evaluated our method using available OWL and OWL EL reasoners. While OWL reasoners may reason over OWL EL ontologies, EL reasoners should implement tractable (i.e. polynomial time) algorithms. The reasoners we investigated are listed in Table 3 along with whether they process EL constructs, implement polynomial time reasoning, implement the Manchester OWL API (Horridge et al., 2007) and support queries for arbitrary class descriptions (e.g. queries for anonymous classes). We evaluated the following reasoners: FaCT++ (Tsarkov and Horrocks, 2006), HermiT (Motik et al., 2009a), Pellet (Sirin and Parsia, 2004), ELLY (http://elly.sourceforge.net/), CEL and JCEL (Baader et al., 2006a). HermiT and FaCT++ support general purpose algorithms for reasoning over OWL that are not guaranteed to terminate in polynomial time. ELLY does not support recent versions of the OWL API, while CEL and JCEL do not support queries for anonymous classes. The algorithm used by Pellet guarantees polynomial time only for a subset of OWL EL. Consequently, while no reasoner exactly satisfies our requirements, Pellet, ELLY and CEL provide the closest match to them. To utilize the potential that EL can bring to the ontology-based applications, we focus on the Pellet-compliant subset of EL in the EL Vira software application.
Table 3.
Evaluated OWL-EL reasoners
| Reasoner | EL support | Polynomial time | OWLAPI support | Anonymous classes |
|---|---|---|---|---|
| ELLY | ✓ | ✓ | # | ✓ |
| HermiT | ✓ | ✗ | ✓ | ✓ |
| Pellet | ✓ | # | ✓ | ✓ |
| CEL | # | ✓ | ✓ | ✗ |
| FaCT++ | # | ✗ | ✓ | ✓ |
| JCEL | # | ✓ | ✓ | ✗ |
‘✓’ means that a requirement is satisfied, ‘✗’ means it is not satisfied and ‘#’ means it is partially satisfied.
2.3 Conversion method
An OWL ontology consists of a set of axioms Ax. Using inference in the description logic underlying OWL, the deductive closure (Ax)⊢ of these axioms can be constructed: (Ax)⊢ is the smallest set including Ax which is closed under a logical entailment operation ⊢. We chose the operation ⊢ so that it is sound and complete for the logic underlying OWL (Horrocks et al., 2006). As a result, the set (Ax)⊢ is the set of all statements in OWL that can be inferred from Ax.
The OWL EL profile is a syntactic subset of OWL, and we define the set ((Ax)⊢)EL as the largest subset of (Ax)⊢ which contains only statements in OWL EL. The task in our modularization approach is to find a finite subset AxEL of ((Ax)⊢)EL such that a large (or maximal) set of statements from ((Ax)⊢)EL can be inferred from AxEL.
For example, an ontology of abnormalities can contain two classes1: Abnormality of appendix and Absence of appendix. An Abnormality of appendix is a property of entities that have no Normal appendix as part, while an Absence of appendix is a property of entities that have no Appendix as part. Furthermore, Normal appendix is a subclass of Appendix. The set of axioms Ax for this ontology consists of:

Based on these axioms, we can use inference in OWL to derive:
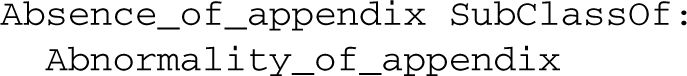
Of these four statements, two are expressed in OWL EL: Absence_of_appendix SubClassOf: Abnormality_of_appendix and Normal_appendix SubClassOf: Appendix. These two statements can be retained in an EL compliant subset of the ontology.
The number of OWL EL statements that can be derived from a set of axioms is usually infinite. Consequently, in our implementation, we rely on predefined patterns to identify the EL statements we retain. The patterns are based on those used in the Manchester OWL API (Horridge et al., 2007) to generate inferred axioms for a given ontology:
two named classes are subclasses of, equivalent to or disjoint from each other;
a named class is a subclass of an existential restriction asserted in one of its (asserted or inferred) super-classes;
a named individual is an instance of a named class;
a named data/object property is a sub-property or equivalent property of another data/object property; and
an object property is inferred to be transitive or reflexive.
2.4 Implementation
The EL Vira software package, available under the GNU General Public License from http://el-vira.googlecode.com, is capable of identifying whether an ontology is within the OWL EL profile or the Pellet-compliant subset of OWL EL, and can convert OWL ontologies to OWL EL. It does so by reading an OWL ontology using the Manchester OWL API (Horridge et al., 2007) and subsequently classifying the ontology using an automated OWL reasoner. The OWL EL ontology is created by copying only the statements allowed in OWL EL from the inferred model of the ontology into the new OWL ontology. In this step, each axiom is analyzed with respect to its expressivity, and only those axioms expressed in OWL EL are copied.
In cases where it is either impossible or unfeasible to classify an OWL ontology using an automated reasoner (e.g. the ontology is in OWL-Full), it may be desirable to create an EL ontology from the asserted axioms alone. This is implemented in a separate application that is combined with the EL Vira software package.
Since many EL reasoners only support a subset of the OWL EL profile, El Vira can be configured to use a custom OWL profile using the -p parameter. Using this approach, we specified the subset supported by the Pellet EL reasoner, which does not support datatype and annotation properties as well as limits the use of class disjointness and different individuals declarations. Annotation and datatype properties may explicitly be ignored, when required, using the -a parameter. Since inference of disjointness axioms is time consuming, these must explicitly be enabled with the -d parameter. The list of parameters and examples can be found on the EL Vira project web site. EL Vira is implemented in Groovy and can be used with the HermiT (Motik et al., 2009a), Fact++ (Tsarkov and Horrocks, 2006) and Pellet (Sirin and Parsia, 2004) Java libraries. FaCT++ support requires that the FaCT++ Java Native Interface library is available in the Java library path.
3 RESULTS AND DISCUSSION
3.1 Correctness and completeness of translation
EL Vira extracts a subset of the inferred axioms of an ontology without adding any axioms to the created EL ontology that could not be previously derived. Furthermore, EL Vira neither adds nor removes any named classes or relations to an ontology. Consequently, monotonicity of the first-order logic (Barwise and Etchemendy, 2002) guarantees the correctness of the conversion, i.e. that no inferences can be made from the reduced theory that were not possible before. However, when the domain and range of an object property in the asserted ontology are disjoint, object properties are created as partial orders, i.e. as irreflexive, transitive, asymmetric properties. Consequently, in the converted ontologies, many properties are declared as transitive. For example, the has-function relation may have as domain Material object and as range Function (Burek et al., 2006), and the classes Material object and Function are assumed to be disjoint. Transitivity states that, if x has-function y and y has-function z, then x has-function z. This condition will always be true for the has-function relation, since x has-function y implies that y is a function, y has-function z implies that y is a material object, and the disjointness of the classes Material object and Function does not allow both statements to be true. Therefore, transitivity of has-function is not incorrect, because transitivity could never be invoked. However, since the additional transitive object properties may cause confusion for ontology users, we have included the option to remove them in the EL Vira software.
The completeness of the conversion is an open problem. When a finite set of axioms is asserted in an ontology, an infinite number of statements can be inferred. An infinite subset of these inferred statements can be represented in EL. Our conversion algorithm extracts only a finite subset. Ideally, this subset would be chosen in such a way that all EL statements that were derivable in the original ontology can be derived from the chosen subset. It is subject to future research to determine whether and how this is theoretically possible, and to extend the EL Vira software to accommodate these results.
3.2 Loss of expressivity
The conversion of an OWL ontology into the OWL EL profile results in a significant loss of expressivity. In particular, negation, union and universal quantifications can no longer be used in OWL EL, and several axiom types for object properties are not available. However, many biomedical ontologies, in particular those available from the OBO Foundry (Smith et al., 2007) and not listed in Table 2, do not currently utilize these features. Therefore, these ontologies can be used in OWL EL without any loss of expressive power.
Negation is of particular importance in phenotype ontologies to allow the description of abnormality or absence (Hoehndorf et al., 2007, 2010b). Within biomedical ontologies, a group of lacks relations can be used to express negation (Ceusters et al., 2006; 2010c), and these relations are applied in the Protein Ontology and the Celltype Ontology to assert that, for example, instances of some protein class have not undergone a certain modification. Upon conversion to OWL EL using EL Vira, the axioms containing negation will be lost. However, if a class is restricted through an axiom that involves negation and this axiom leads to the inference of a new subclass axiom, such an axiom will be added to the ontology. We have provided such an example in Section 2.3.
Furthermore, axioms involving class unions (‘or’) are not available in OWL EL. Such axioms are used in some biomedical ontologies to group several classes under a common superclass. For example, the Celltype Ontology contains a class CD7-negative lymphoid progenitor OR granulocyte monocyte progenitor (CL:0001012), which is defined as the union of Granulocyte monocyte progenitor cell (CL:0000557) and CD7-negative lymphoid progenitor cell (CL:0001027). This definition would be lost in an OWL EL version of the ontology. Since the conversion to OWL EL using EL Vira utilizes automated reasoning, two inferences of the original definition will be added to the converted OWL EL ontology: that both the classes Granulocyte monocyte progenitor cell and CD7-negative lymphoid progenitor cell are subclasses of CD7-negative lymphoid progenitor OR granulocyte monocyte progenitor.
The loss of universal quantification is of particular importance in the representation of functions and dispositions. Universal quantification is necessary to link functions or dispositions to the processes that may realize them (Schulz et al., 2009a; Schulz et al., 2009b), and is used primarily in ontologies of disease such as the Malaria Ontology (Topalis et al., 2010). Although such axioms can be used to infer subclass relations which will be maintained through the use of EL Vira, the link between functions or dispositions and the processes that may realize them will be lost through the conversion to OWL EL.
Finally, several types of axioms for relations can no longer be expressed and used for reasoning in OWL EL. In particular, symmetric, asymmetric, functional and inverse object properties can no longer be used. Such axioms for relations are asserted in the OBO Relationship Ontology (Smith et al., 2005) and used in several biomedical ontologies. For example, the inheres-in relation between a quality and the entity of which it is a quality is functional: a quality can inhere in at most one entity. The functionality of inheres-in is used in phenotype ontologies to infer subclass relations and verify consistency (Hoehndorf et al., 2010b). While the inferred subclass relations are maintained, functionality could not be utilized for consistency verification in OWL EL alone.
Through the use of EL Vira, the taxonomy and existential restrictions placed on classes in biomedical ontologies are maintained. Therefore, algorithms and analysis methods that only rely on an ontology's graph structure (e.g. the ontology's taxonomy or partonomy) experience no information loss.
3.3 Performance evaluation
We evaluated the EL Vira approach by converting the Ontology of Biomedical Investigations (OBI) (Courtot et al., 2008) and the Foundational Model of Anatomy (FMA) into OWL EL. We show how many axioms are retained in OBI and how the speed of automated reasoning is improved by several orders of magnitude when the EL subset of the ontologies is used.
The OBI (Courtot et al., 2008) is an ontology containing terms that are relevant to biomedical experiments, assays and their reporting. It is developed in OWL and contains 2639 classes, 77 object properties, 6 data properties and 89 individuals. OBI contains 3538 subclass axioms, 158 equivalent class axioms, 6047 disjointness axioms as well as a number of axioms that restrict object and data properties. Table 4 lists the number of asserted/inferred axioms contained in OBI, the number of axioms after the EL Vira conversion into an OWL EL ontology and the number of axioms in the Pellet-compliant OWL EL ontology.
Table 4.
Number of entities in the OBI using different settings of EL Vira
| A/I | EL | EL (PC) | ||
|---|---|---|---|---|
| OWL entities | Classes | 2639/2639 | 2639 | 2639 |
| Object properties | 77/78 | 78 | 78 | |
| Data properties | 6/7 | 7 | 0 | |
| Individuals | 89/89 | 89 | 89 | |
| Class axioms | Class inclusion axioms | 3538/3464 | 3464 | 2713 |
| Class equivalence axioms | 158/111 | 111 | 0 | |
| Class disjointness axioms | 6047/6047 | 6047 | 0 | |
| Object property axioms | Object property inclusion axioms | 35/77 | 77 | 77 |
| Transitive object property axioms | 15/41 | 41 | 41 | |
| Domain restrictions | 39/39 | 39 | 0 | |
| Range restrictions | 40/38 | 38 | 0 | |
| Inverse object property axioms | 23/23 | 0 | 0 | |
| Functional object property axioms | 3/9 | 0 | 0 | |
| Individual assertions | Class assertion axioms | 182/648 | 648 | 647 |
| Object property assertion axioms | 47/75 | 75 | 75 | |
| Data property assertion axioms | 1/1 | 1 | 0 | |
| Different Individuals axioms | 3/3 | 3 | 0 |
‘A’ represents the asserted entities, and both the number of directly asserted as well as the number of inferred entities it provides. The ‘EL’ column provides the number of entities retained after the conversion to EL, while ‘EL (PC)’ lists the number of entities obtained using Pellet-compliant settings of EL Vira.
While certain assertions are lost in the EL translation, the number of lost axioms does not directly correspond to the number of lost inferences. For example, we note that some subclass axioms are removed by the automated reasoner, e.g. redundant subclass assertions: if C is declared to be a subclass of B and A, and B is declared as a subclass of A, then an automated reasoner will remove the redundant subclass assertion between C and A.
We measured the performance of different reasoners applied to different versions of the ontologies. These tests were performed on hardware consisting of two Intel® Xeon® 2.4 GHz quad-core CPUs with 24 GB memory. Despite the availability of these resources, we were not able to classify the FMA and consequently created the OWL EL version of the FMA without the use of an OWL reasoner.
Table 5 shows the performance results for classifying these ontologies using different reasoners and the performance results for queries over the ontologies when querying for direct subclasses of owl:Thing and for direct superclasses of owl:Nothing.
Table 5.
Classification time and query time in seconds for the OBI and FMA using the Pellet and HermiT reasoners
| OBI |
FMA |
|||||
|---|---|---|---|---|---|---|
| Plain | EL | EL(PC) | Plain | EL | ||
| Classification | Pellet | 55.6 | 28.3 | 0.4 | N/A | 38.2 |
| HermiT | 180.2 | 0.8 | 0.6 | N/A | 467.1 | |
| Query | Pellet | 493.2 | 77.5 | 0.4 | N/A | 0.4 |
| HermiT | 1.0 | 0.0 | 0.0 | N/A | 0.3 | |
A ‘N/A’ signifies that we were not able to classify the ontology using this reasoner. Response times listed as 0.0 indicate that the measured time was below 0.05 s. The query was performed for direct subclasses of owl:Thing and direct super-classes of owl:Nothing.
Our results demonstrate that our method decreased the number of axioms in the ontologies that can be utilized for automated reasoning, while greatly improving the speed of reasoning. The number of axioms which are removed due to the conversion to EL is dependent on the ontologies.
While the use of EL Vira and the application of OWL EL reasoning will invariably result in a loss of expressivity for expressive OWL ontologies, several important axioms types continue to be available in EL. In particular, the is-a hierarchy that can be inferred by an automated reasoner based on expressive axioms in OWL is retained through the use of EL Vira. Furthermore, class axioms involving existential restrictions, which make up a large fraction of the axioms in biomedical ontologies, remain available in EL versions of ontologies. Through a conversion to EL, ontologies that could not be classified before, like the FMA, can now be classified and used for inferences.
3.4 Toward a model for ontology development and integration
Although the decreased time complexity of EL makes it suitable for large-scale semantic applications, many biomedical ontologies do not utilize EL directly. Instead, the semantics of the ontologies corresponds to a more expressive subset of OWL enabling them to serve as a reference for the meaning of terms in a vocabulary. The advantages of such an approach is that the ontologies can be utilized for consistency verification, inferences and queries, classification and knowledge discovery (Wolstencroft et al., 2006). In particular, negation and disjointness in combination with domain and range restrictions of object and data properties can be used for verifying the consistency of data. For these purposes, an expressive language is desirable and should not be sacrificed.
On the other hand, when ontologies are employed in information systems, their full expressivity can often not be used because these systems rely on fast response times. In particular, when multiple ontologies are combined and integrated, the complexity of OWL reasoning exceeds the capabilities of current reasoners. Due to the established theoretical upper bounds for reasoning over OWL, future automated reasoners will face the same limitations. Consequently, current ontology-based information systems in biology either ignore formal semantics entirely or provide case-based interpretations encoded in database schemata or software code.
We have demonstrated that formalisms with lower complexity, such as OWL EL, can be utilized in software applications to perform fast queries over large knowledge bases. Although this reduction in expressivity greatly improves the performance of reasoning, it leads to limited utility of ontologies for consistency verification and expressive inferences. Consequently, biomedical ontologies should continue to be developed in expressive formal languages, while the use of our method allows the ontologies to be automatically transformed in a less expressive representation that can be efficiently utilized in software implementations.
4 CONCLUSIONS
Due to the large size and number of biomedical ontologies as well as the high complexity of reasoning in OWL, current OWL reasoners are often unable to process biomedical ontologies. Automated reasoning is necessary to detect errors in ontologies and exploit them for knowledge discovery and retrieval. We described a modularization approach in which ontologies are automatically converted into an OWL profile that enables tractable reasoning. No class or relation is removed from the OWL ontology through this method and inferences that affect the ontologies' taxonomy are maintained. We implemented this method in the EL Vira software. The application of our method and software creates a common layer of interoperability based on which biomedical ontologies can achieve their declared goal of facilitating the semantic integration of biomedical data and research results.
Funding: Funding for R.H. and S.W. was provided by the European Commission's 7th Framework Programme, RICORDO project (grant number 248502). Funding for M.D. was provided by a NSERC Discovery Grant. Funding for A.O. and D.R.-S. was provided by the European Bioinformatics Institute. Funding for P.S. was provided by an National Institutes of Health (grant number R01 HG004838-02). Funding for G.V.G. was provided by BBSRC (grant BBG0043581).
Conflict of Interest: none declared.
Footnotes
1The example is adopted from the phenotype ontology available at http://bioonto.de/uploads/Main/appendix.owl.
REFERENCES
- Ashburner M., et al. Gene ontology: tool for the unification of biology. Nat. Genet. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baader F., et al. Proceedings of the Nineteenth International Joint Conference on Artificial Intelligence IJCAI-05. Edinburgh, UK: Morgan-Kaufmann Publishers; 2005. Pushing the ℰℒ envelope. [Google Scholar]
- Baader F., et al. CEL—a polynomial-time reasoner for life science ontologies. In: Furbach U., Shankar N., editors. Proceedings of the 3rd International Joint Conference on Automated Reasoning (IJCAR'06) Springer; 2006a. pp. 287–291. 4130 of Lecture Notes in Artificial Intelligence. [Google Scholar]
- Baader F., et al. Proceedings of the 2006 International Workshop on Description Logics (DL2006) CEUR-WS; 2006b. Efficient reasoning in ℰℒ+ [Google Scholar]
- Bard J., et al. An ontology for cell types. Genome Biol. 2005;6:R21. doi: 10.1186/gb-2005-6-2-r21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barwise J., Etchemendy J. Center for the Study of Language and Information (CSLI) Stanford, USA: 2002. Language, Proof and Logic. [Google Scholar]
- Battista A.D.L., Dumontier M. Proceedings of the 6th International Workshop on OWL: Experiences and Directions (OWLED 2009) Vol. 529. Innsbruck, Austria: 2009. A platform for reasoning with OWL-EL knowledge bases in a peer-to-peer environment. CEURS-WS.org. [Google Scholar]
- Burek P., et al. A top-level ontology of functions and its application in the open biomedical ontologies. Bioinformatics. 2006;22:e66–e73. doi: 10.1093/bioinformatics/btl266. [DOI] [PubMed] [Google Scholar]
- Ceusters W., et al. Referent tracking: the problem of negative findings. Stud. Health Technol. Inform. 2006;124:741–746. [PubMed] [Google Scholar]
- Courtot M., et al. The OWL of biomedical investigations. In: Dolbear C., et al., editors. Proceedings of the Fourth OWLED Workshop on OWL: Experiences and Directions. Innsbruck, Aachen: 2008. CEUR-WS.org. [Google Scholar]
- Gkoutos G.V., et al. Building mouse phenotype ontologies. Pac. Symp. Biocomput. 2004;9:178–189. doi: 10.1142/9789812704856_0018. [DOI] [PubMed] [Google Scholar]
- Golbreich C., et al. The foundational model of anatomy in owl: Experience and perspectives. Web Semant. 2006;4:181–195. doi: 10.1016/j.websem.2006.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grau B., et al. Owl 2: The next step for owl. Web Semant. 2008;6:309–322. [Google Scholar]
- Gruber T.R. Towards principles for the design of ontologies used for knowledge sharing. In: Guarino N., Poli R., editors. Formal Ontology in Conceptual Analysis and Knowledge Representation. Deventer, The Netherlands: Kluwer Academic Publishers; 1993. [Google Scholar]
- Guarino N. Formal ontology and information systems. In: Guarino N., editor. Proceedings of the 1st International Conference on Formal Ontologies in Information Systems. IOS Press; 1998. pp. 3–15. [Google Scholar]
- Hayamizu T.F., et al. The adult mouse anatomical dictionary: a tool for annotating and integrating data. Genome Biol. 2005;6:R29. doi: 10.1186/gb-2005-6-3-r29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoehndorf R., et al. Representing default knowledge in biomedical ontologies: application to the integration of anatomy and phenotype ontologies. BMC Bioinformatics. 2007;8:377. doi: 10.1186/1471-2105-8-377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoehndorf R., et al. Applying the functional abnormality ontology pattern to anatomical functions. J. Biomed. Semant. 2010a;1:4. doi: 10.1186/2041-1480-1-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoehndorf R., et al. Interoperability between phenotype and anatomy ontologies. Bioinformatics. 2010b;26:3112–3118. doi: 10.1093/bioinformatics/btq578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoehndorf R., et al. Relations as patterns: Bridging the gap between OBO and OWL. BMC Bioinformatics. 2010c;11:441. doi: 10.1186/1471-2105-11-441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horridge M., et al. Proceedings of the OWLED 2007 Workshop on OWL: Experiences and Directions. Vol. 258. Innsbruck, Austria: 2007. Igniting the OWL 1.1 touch paper: The OWL API. CEUR-WS.org. [Google Scholar]
- Horrocks I., et al. Practical reasoning for very expressive description logics. Logic J. IGPL. 2000;8:239–264. [Google Scholar]
- Horrocks I., et al. Proceedings of the 10th International Conference on Principles of Knowledge Representation and Reasoning (KR2006) Menlo Park, California, USA: AAAI Press; 2006. The even more irresistible SROIQ; pp. 57–67. [Google Scholar]
- Horrocks I. Technical report. University of Manchester; 2007. Obo flat file format syntax and semantics and mapping to owl web ontology language. [Google Scholar]
- Motik B., et al. Hypertableau reasoning for description logics. J. Art. Intell. Res. 2009a;36:165–228. [Google Scholar]
- Motik B., et al. OWL 2 Web Ontology Language: profiles. Recommendation, World Wide Web Consortium (W3C); 2009b. Available at http://www.w3.org/TR/owl2-profiles/ [Google Scholar]
- Mungall C.J., et al. Cross-product extensions of the gene ontology. J. Biomed. Inform. 2010a doi: 10.1016/j.jbi.2010.02.002. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mungall C.J., et al. Evolution of the sequence ontology terms and relationships. J. Biomed. Inform. 2010b doi: 10.1016/j.jbi.2010.03.002. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mungall C., et al. Integrating phenotype ontologies across multiple species. Genome Biol. 2010c;11:R2. doi: 10.1186/gb-2010-11-1-r2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mutharaju R., et al. Proceedings of the 23rd International Workshop on Description Logics (DL2010) Vol. 573. Innsbruck, Austria: 2010. A MapReduce algorithm for EL+ pp. 464–474. CEUR-WS.org. [Google Scholar]
- Noy N.F., et al. Bioportal: ontologies and integrated data resources at the click of a mouse. Nucleic Acids Res. 2009;37:W170–W173. doi: 10.1093/nar/gkp440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rector A.L., Brandt S. Why do it the hard way? The case for an expressive description logic for SNOMED. J. Am. Med. Inform. Assoc. 2008;15:744–751. doi: 10.1197/jamia.M2797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson P. N., et al. The human phenotype ontology: a tool for annotating and analyzing human hereditary disease. Am. J. Hum. Genet. 2008;83:610–615. doi: 10.1016/j.ajhg.2008.09.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosse C., Mejino J.L.V. A reference ontology for biomedical informatics: the Foundational Model of Anatomy. J. Biomed. Inform. 2003;36:478–500. doi: 10.1016/j.jbi.2003.11.007. [DOI] [PubMed] [Google Scholar]
- Schulz S., et al. SNOMED reaching its adolescence: Ontologists' and logicians' health check. Int. J. Med. Inform. 2009a;78(Suppl. 1):S86–S94. doi: 10.1016/j.ijmedinf.2008.06.004. [DOI] [PubMed] [Google Scholar]
- Schulz S., et al. Strengths and limitations of formal ontologies in the biomedical domain. RECIIS - Electronic Journal of Communication, Information & Innovation in Health. 2009b;3:31–45. doi: 10.3395/reciis.v3i1.241en. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sirin E., Parsia B. Pellet: an OWL DL reasoner. In: Haarslev V., Möller R., editors. Proceedings of the 2004 International Workshop on Description Logics. Vol. 104. Aachen, Germany: 2004. DL2004, Whistler, British Columbia, Canada, June 6–8, of CEUR Workshop Proceedings. [Google Scholar]
- Smith B., et al. Relations in biomedical ontologies. Genome Biol. 2005;6:R46. doi: 10.1186/gb-2005-6-5-r46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith B., et al. The OBO Foundry: coordinated evolution of ontologies to support biomedical data integration. Nat. Biotech. 2007;25:1251–1255. doi: 10.1038/nbt1346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith C.L., et al. The mammalian phenotype ontology as a tool for annotating, analyzing and comparing phenotypic information. Genome Biol. 2004;6:R7. doi: 10.1186/gb-2004-6-1-r7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suntisrivaraporn B. Proceedings of the 2nd Mahasarakham International Workshop on AI (MIWAI'08) Mahasarakham, Thailand: Mahasarakham University; 2008. Empirical evaluation of reasoning in lightweight DLs on life science ontologies. [Google Scholar]
- Tobies S. The complexity of reasoning with cardinality restrictions and nominals in expressive description logics. J. Artif. Int. Res. 2000;12:199–217. [Google Scholar]
- Topalis P., et al. A set of ontologies to drive tools for the control of vector-borne diseases. J. Biomed. Inform. 2010 doi: 10.1016/j.jbi.2010.03.012. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsarkov D., Horrocks I. FaCT++ description logic reasoner: System description. In: Furbach U., Shankar N., editors. Automated Reasoning: Proceedings of the Third International Joint Conference. Vol. 4130. Berlin: Springer; 2006. IJCAR 2006, Seattle, Washington, USA, August 17–20 of Lecture Notes in Computer Science. [Google Scholar]
- Wolstencroft K., et al. Protein classification using ontology classification. Bioinformatics. 2006;22:e530–e538. doi: 10.1093/bioinformatics/btl208. [DOI] [PubMed] [Google Scholar]
