Abstract
We describe the third generation of the CAP sequence assembly program. The CAP3 program includes a number of improvements and new features. The program has a capability to clip 5′ and 3′ low-quality regions of reads. It uses base quality values in computation of overlaps between reads, construction of multiple sequence alignments of reads, and generation of consensus sequences. The program also uses forward–reverse constraints to correct assembly errors and link contigs. Results of CAP3 on four BAC data sets are presented. The performance of CAP3 was compared with that of PHRAP on a number of BAC data sets. PHRAP often produces longer contigs than CAP3 whereas CAP3 often produces fewer errors in consensus sequences than PHRAP. It is easier to construct scaffolds with CAP3 than with PHRAP on low-pass data with forward–reverse constraints.
The shotgun sequencing strategy has been used widely in genome sequencing projects. A major phase in this strategy is to assemble short reads into long sequences. A number of DNA sequence assembly programs have been developed (Staden 1980; Peltola et al. 1984; Huang 1992; Smith et al. 1993; Gleizes and Henaut 1994; Lawrence et al. 1994; Kececioglu and Myers 1995; Sutton et al. 1995; Green 1996). The FAKII program provides a library of routines for each phase of the assembly process (Larson et al. 1996). The GAP4 program has a number of useful interactive features (Bonfield et al. 1995). The PHRAP program clips 5′ and 3′ low-quality regions of reads and uses base quality values in evaluation of overlaps and generation of contig sequences (Green 1996). TIGR Assembler has been used in a number of megabase microbial genome projects (Sutton et al. 1995). Continued development and improvement of sequence assembly programs are required to meet the challenges of the human, mouse, and maize genome projects.
We have developed the third generation of the CAP sequence assembly program (Huang 1992). The CAP3 program includes a number of improvements and new features. A capability to clip 5′ and 3′ low-quality regions of reads is included in the CAP3 program. Base quality values produced by PHRED (Ewing et al. 1998) are used in computation of overlaps between reads, construction of multiple sequence alignments of reads, and generation of consensus sequences. Efficient algorithms are employed to identify and compute overlaps between reads. Forward–reverse constraints are used to correct assembly errors and link contigs. Results of CAP3 on four BAC data sets are presented. The performance of CAP3 was compared with that of PHRAP on a number of BAC data sets. PHRAP often produces longer contigs than CAP3 whereas CAP3 often produces fewer errors in consensus sequences than PHRAP. It is easier to construct scaffolds with CAP3 than with PHRAP on low-pass data with forward–reverse constraints.
An unusual feature of CAP3 is the use of forward–reverse constraints in the construction of contigs. A forward–reverse constraint is often produced by sequencing of both ends of a subclone. A forward–reverse constraint specifies that the two reads should be on the opposite strands of the DNA molecule within a specified range of distance. By sequencing both ends of each subclone, a large number of forward–reverse constraints are produced for a cosmid or BAC data set. A difficulty with use of forward–reverse constraints in assembly is that some of the forward–reverse constraints are incorrect because of errors in lane tracking and cloning. Our strategy for dealing with this difficulty is based on the observation that a majority of the constraints are correct and wrong constraints usually occur randomly. Thus, a few unsatisfied constraints in a contig may not be sufficient to indicate an assembly error in the contig. However, if a sufficient number of constraints are all inconsistent with a join in a contig and all support an alternative join, it is likely that the current join is an error, and the alternative join should be made.
METHODS
The assembly algorithm consists of three major phases (Fig. 1). In the first phase, 5′ and 3′ poor regions of each read are identified and removed. Overlaps between reads are computed. False overlaps are identified and removed. In the second phase, reads are joined to form contigs in decreasing order of overlap scores. Then, forward–reverse constraints are used to make corrections to contigs. In the third phase, a multiple sequence alignment of reads is constructed and a consensus sequence along with a quality value for each base is computed for each contig. Base quality values are used in computation of overlaps and construction of multiple sequence alignments. We describe each phase in detail below.
Figure 1.

Major steps of the assembly algorithm.
Fast Identification of Pairs of Reads with an Overlap
A fast method is designed to find pairs of sequence reads that overlap. Specifically, let f1,f2,... be all the input reads in given orientation and let rx be the reverse complement of read fx. The method quickly finds pairs of reads fx and fy with x < y that overlap and pairs of reads rx and fy with x < y that overlap. Note that each identified pair of reads represents two symmetric overlaps because of a reverse complementary relationship. An overlap between reads fx and fy is symmetric to one between reads rx and ry and an overlap between reads rx and fy to one between reads fx and ry.
To determine quickly whether two reads have a potential overlap, an overlapping alignment between two reads is simplified as an ordered chain of segment pairs, where each segment pair corresponds to an ungapped portion of sufficient length of the alignment. A largest-scoring chain of segment pairs between two reads can be quickly computed by use of a BLAST-like technique (Altschul et al. 1990; Huang 1996b). A pair of reads has a potential overlap if the reads contain a chain of similarity score greater than a score cutoff. One approach to finding pairs of reads with a potential overlap is to apply the BLAST-like technique to each pair of reads fx and fy with x < y and each pair of reads rx and fy with x < y. However, this approach goes through a large number of pairs of reads that may not overlap. Below, we describe a more efficient approach.
The sequences of all reads f1,f2, ... are concatenated together with a special character inserted at every read boundary. The resulting sequence is called the combined sequence. Then, the following procedure is performed once for each read fx to find pairs of reads fx and fy, x < y, with a potential overlap and once for each read rx to find pairs of reads rx and fy, x < y, with a potential overlap. Let the current read g be fx or rx. High-scoring chains of segment pairs between the read g and the combined sequence are computed. The special boundary character is used to make sure that a chain consists only of segment pairs from the same read in the combined sequence. To find the corresponding read fy in the combined sequence for a chain, a binary search is performed in a sorted list of the start and end positions of each read in the combined sequence. Note that the chains between the read g and any read fy with x ≥ y in the combined sequence are ignored.
For each pair of reads with a potential overlap, a minimum band of diagonals in the dynamic programming matrix is determined to cover all the chains of score greater than the cutoff between the reads. Here, a diagonal k in the dynamic programming matrix consists of all entries (i,j) such that j − i = k (Smith and Waterman 1981). A segment pair beginning with position i of one read and position j of the other read is said to occur on diagonal j − i. A band of diagonals in the matrix covers a chain of segment pairs if each segment pair in the chain occurs on a diagonal inside the band. The band of diagonals for a pair of reads with a potential overlap is later used for efficient computation of the overlap.
Clipping of Low-Quality Regions
Low-quality end regions of reads are located and removed as follows. Both base quality values and sequence similarities are used to compute 5′ and 3′ clipping positions of reads. Our strategy is based on the following definition of good regions of a read. Any sufficiently long region of high-quality values that is highly similar to a region of another read is defined to be good. In addition, any sufficiently long region that is highly similar to a good high-quality region of another read is defined to be good. The 3′ clipping position of a read is the maximum of 3′ end positions of good regions of the read. The 5′ clipping position of a read is the minimum of 5′ end positions of good regions of the read. Figure 2 illustrates computation of the 5′ and 3′ clipping positions of a read. Regions of reads with a strong sequence similarity to other reads are located by computing the start and end positions of an optimal local alignment for each pair of reads with a potential overlap. For efficiency, computation with the algorithm of Smith and Waterman (1981) is restricted to a band of diagonals in the dynamic programming matrix (Pearson and Lipman 1988; Green 1996). Recall that our fast method for finding each pair of reads with a potential overlap reports a band of diagonals for the pair. The band is expanded in both directions by a certain number of bases, which can be specified by the user. A local alignment computation is performed over the expanded band of diagonals.
Figure 2.
Computation of the 5′ and 3′ clipping positions of read f. Read f has high local similarities to reads g and h. A pair of broken lines shows the start and end positions of a similarity. A thick line indicates the high-quality region of a read.
The local alignment algorithm of Smith and Waterman (1981) is generalized to use base quality values. The quality value of a base is q = −10 × log10(p), where p is the estimated error probability for the base (Ewing and Green 1998). Match scores, mismatch scores, and gap penalties are all weighted by the quality values of the bases involved. The intention for using base quality values is that matches at bases of high quality values should receive a large positive score, differences at bases of high quality values a large negative score, but, matches and differences at bases of low quality values should receive small positive and negative scores, respectively. Let a positive integer m be a match score factor, let a negative integer n be a mismatch score factor, and let a positive integer g be a gap extension penalty factor. A match at bases of quality values q1 and q2 is given a score of m * min(q1,q2). A mismatch at bases of quality values q1 and q2 is given a score of n * min(q1,q2). A base of quality value q1 in a gap is given an extension score of −g * min(q1,q2), where q2 is the quality value of the base in the other sequence immediately before the gap if there is a base before the gap and the quality value of the base immediately after the gap otherwise. Another possible definition for q2 is that q2 is the smaller of the quality values of the bases in the other sequence immediately before and after the gap. The second definition is not currently used in the code and will be made available as an option in the future. The score of a gap is the sum of extension scores of each base in the gap minus a gap open penalty. For simplicity, the gap open penalty is a positive integer independent of base quality values. The similarity score of an alignment is the sum of scores of each match, each mismatch, and each gap.
For chimeric reads, their 5′ and 3′ clipping positions are computed in a different way. Chimeric reads are identified by use of the method discussed in Huang (1996a). For each chimeric read, a nonchimeric, good region of the maximum length is found. The 5′ and 3′ clipping positions of the read are the start and end positions of the region, respectively.
Computation and Evaluation of Overlaps
We first describe a method for computing overlaps between reads and then present a method for identifying false overlaps. From now on, a clean read or a read means the good region of the raw read after the 5′ and 3′ poor regions are removed. An overlap between two reads is defined as a global alignment of the reads with the maximum similarity score (Huang 1992). The definition of an overlap as an optimal global alignment of two clean reads instead of as an optimal local alignment between two raw reads is useful for identifying false overlaps. An optimal global alignment may show that some good regions of the reads are not similar, which indicates that the overlap is false, whereas an optimal local alignment shows only similar regions.
For each pair of reads with a potential overlap, a band of diagonals, centered at the start position of the optimal local alignment computed previously, is formed (Fig. 3). The band width is twice the band expansion size used in the local alignment computation. A global alignment with the maximum similarity score is computed over the band. A divide–conquer technique is used to perform the banded computation in linear space (Chao et al. 1992). As in the local alignment computation, match and difference scores are weighted by base quality values. The global alignment is the overlap between the reads. The length, similarity score, and percent identity of the overlap are defined to be those of the alignment, respectively.
Figure 3.
Computation of a global alignment of clean reads f and g with the maximum score over a band. The rectangle represents the dynamic programming matrix, with the rows corresponding to the bases of read f and the columns to the bases of read g. The band is indicated by a shaded area and the start position of an optimal local alignment between raw reads f and g is indicated by a dot.
Each overlap is evaluated by five measures. If the overlap fails under any of the five measures, then the overlap is not considered in construction of contigs. The first three measures determine whether the overlap satisfies the minimum requirements on length, percent identity, and similarity score.
The fourth measure examines the differences of the overlap at bases of high quality values. If the overlap contains a sufficient number of differences at bases of high-quality values, then the overlap is probably false. Specifically, let an integer b be a high quality value cutoff and let an integer d be a quality difference score cutoff. For a difference of the overlap at bases of quality values q1 and q2, the score at the difference is max[0, min(q1,q2) − b]. The use of the term zero implies that no difference is counted at bases of quality values less than b. The quality difference score of the overlap is the sum of scores at each difference. If the quality difference score of the overlap exceeds d, then the overlap is removed. For example, with b = 20, an overlap with 15 differences at bases of quality values 40 or higher has a quality difference score of at least 300 and is removed if d = 250. The values for the parameters b and d can be set by the user.
Under the fifth measure, the difference rate of the overlap is examined with respect to the sequencing error rates of the two regions involved in the overlap. The error rate of any region of a read is estimated using the error vector method (Huang 1996a). For any true overlap, the difference rate of the overlap is close to the sum of the error rates of the two regions involved in the overlap. Thus, if the difference rate of an overlap is sufficiently higher than expected, then the overlap is probably false. Let e be the largest clearance between rates of difference. Let r1 be the estimated error rate for one overlap region and let r2 be that for the other region. If the difference rate of the overlap is greater than r1 + r2 + e, then the overlap is removed. The value for the parameter e can be changed by the user. Giving a smaller value to the parameter e causes more overlaps to be removed. The fourth and fifth measures complement each other; the fourth measure depends on base quality values, but the fifth measure does not.
Use of Constraints in Construction of Contigs
The procedure for using constraints in construction of contigs consists of four major steps. In step 1, an initial layout of reads is performed by use of a greedy method in decreasing order of overlap scores (Huang 1996a). In step 2, the quality of the current layout is assessed by checking constraints. The constraint satisfiability information for each part of the current layout is collected. In step 3, a region of the current layout with the largest number of unsatisfied constraints is located such that the unsatisfied constraints are satisfiable by making corrections to the region. If such a region exists, corrections to the region are made and steps 2 and 3 are repeated. Otherwise, the correction procedure is terminated. In step 4, contigs are linked with constraints. Then, each list of linked contigs is reported. Below, we first give some definitions and then describe steps 2–4.
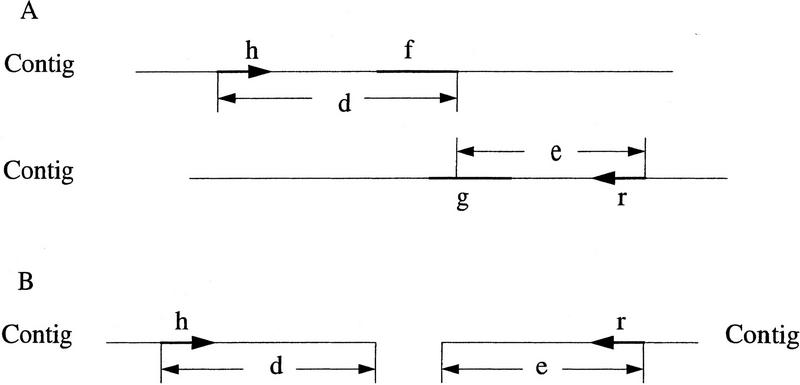
A forward–reverse constraint consists of two reads and two integers that specify a range for the distance between the reads. The constraint is satisfied by a layout if the two reads occur in the same contig, the upstream read is in forward orientation, the downstream read in reverse orientation, and the distance between the two reads is within the given range. Otherwise, the constraint is unsatisfied. An overlap is unused if the overlap is not used in the current layout. Let f → g denote an overlap from read f to read g. An unsatisfied constraint involving reads h and r is satisfiable by an unused overlap f → g if read f occurs downstream of read h (r) in forward orientation in a contig, read g occurs upstream of read r (h) in reverse orientation in a contig, and the sum of the distance between read h (r) in forward orientation and read f and the distance between read g and read r (h) in reverse orientation is within the distance range of the constraint (Fig. 4A). An unsatisfied constraint involving reads h and r is a link between two contigs if read h (r) in the forward orientation occurs in one contig, read r (h) in the reverse orientation occurs in the other contig, and the sum of the distance between read h (r) and the 3′ end of the contig and the distance between the 5′ end of the other contig and read r (h) is less than the maximum distance of the constraint (Fig. 4B). Let u be the minimum number of unsatisfied constraints required to indicate a problem in the layout. The value for u is changeable by the user.
Figure 4.
An unsatisfied constraint involving reads h and r with a distance range of x to y bp. The orientations of reads h and r are indicated by arrows. (A) The constraint is satisfiable by an unused overlap from reads f to g, with x ≤ d + e ≤ y. (B) The constraint serves as a link between two contigs, with d + e ≤ y.
In step 2, every constraint is checked on the current layout. Satisfied constraints are used to compute, for each overlap used in the layout, the number of satisfied constraints that support the overlap. Unsatisfied constraints are partitioned into groups, where all constraints in a group are associated with an unused overlap or a pair of contigs. This is done as follows. For each unsatisfied constraint that is satisfiable by unused overlaps, a unique overlap with the maximum score is selected from the unused overlaps, and the constraint is associated with the overlap. Additional criteria are used to choose only one winner in the case that there are two or more unused overlaps with the maximum score. For each of the remaining unsatisfied constraints, if the constraint is a link between two contigs, then the constraint is associated with the pair of contigs.
In step 3, a group with the largest number of unsatisfied constraints is selected for consideration. First consider the case where the group is associated with an unused overlap f → g. If the number of unsatisfied constraints in the group is greater than the sum of the parameter u, the number of satisfied constraints supporting the used overlap involving f, and the number of satisfied constraints supporting the used overlap involving g, then the layout is corrected by breaking the used overlaps involving f and g, and joining f and g with the overlap f → g. Next, consider the case where the group is associated with a pair of contigs. If the gap between the two contigs can be closed using reads from other regions to make the unsatisfied constraints satisfiable, then the gap closure is implemented. Reads from other regions that are associated by constraints with reads in the two contigs are used to close the gap. If no correction is made to the current layout for the selected group, then the selection process is repeated with the remaining groups of constraints until a correction is made to the current layout or no more group is available for selection.
In step 4, contigs are ordered using constraints as links. Step 2 is performed to obtain groups of unsatisfied constraints that serve as links between contigs. The groups are considered in decreasing order of group size. Let integer v be the minimum number of constraints required to link two contigs. For each group of constraints that are associated with a pair of contigs, if the number of constraints in the group is not less than the parameter v, and neither of the two contigs is already linked to other contigs at the corresponding end, then a link between the contigs is established.
Construction of Alignments and Consensus Sequences
A multiple sequence alignment of reads is constructed for each contig. The construction is performed by repeatedly aligning the next read with the current alignment. The reads are considered in increasing order of their positions in the contig. To produce an accurate alignment, the base quality values of the reads are used in the construction. After an alignment is constructed, a consensus sequence along with a quality value for each base is computed for the contig. For each column of the alignment, a weighted sum of quality values is calculated for each base type and the base type with the largest sum of quality values is taken as the consensus base for the column. The quality value for the consensus base is the sum of quality values for the consensus base type minus the sum of quality values for every other base type. However, if the column contains two base types, each with a very large sum of quality values, then a very low quality value is assigned to the consensus base. The assignment of the low quality value indicates a potential problem often caused by polymorphism or collapsing of highly similar copies of a repetitive element.
A weighted sum of quality values is calculated for each base type as follows. The quality values for the base type are partitioned into two groups, one for each strand. It is assumed that quality values in one group are independent of ones in the other group (Green 1996). The quality values in each group are sorted in decreasing order. The ith value in each group is given a weight of wi. Then a sum of all quality values multiplied by their weights is computed. The following simple set of weights is currently used: w1 = 1.0 and wi = 0.5 for i > 1. For example, consider computing a weighted sum of four quality values 20, 40, 30, and 10 for a base type using the simple set of weights. Assume that the values 20 and 30 are from the plus strand and the values 40 and 10 are from the minus strand. Then the weighted sum of quality values for the base type is 85, where the weight for the values 30 and 40 is 1.0 and the weight for the values 20 and 10 is 0.5. CAP3 quality values for consensus bases are related to estimated error rates for the bases. A proper set of weights will be worked out in the future so that CAP3 quality values accurately correspond to error rates.
We consider aligning one read with the current alignment of reads. For clarity, the current alignment is called a block. Although the block may be very long, a major portion of the block remains unchanged for the rest of the construction. Thus, only the 3′ portion of the block that gets changed is used for alignment. This 3′ portion of the block is replaced by the resulting alignment. In the following, the block means the 3′ portion.
A scoring scheme is introduced that incorporates base quality values into the score of an alignment of the block and the read. In this scheme, several average quality values are computed for each column of the block. Then the average quality values are used along with the quality values of the read to weight match and difference scores. An alignment of the block and the read consists of substitutions, deletion gaps, and insertion gaps. In a substitution, a column of the block is aligned with a base of the read. A deletion gap consists of a number of columns of the block. An insertion gap consists of a number of bases of the read.
Consider a column of the block. Let the column consist of k nonblank characters ci, 1 ≤ i ≤ k. Each ci is in one of A, C, G, T, N, and −, where N denotes any base other than the four regular bases and − is a gap symbol. Let qi be the quality value of ci. If ci is a gap symbol, then qi is the quality value of the base immediately before ci in the same row if such a base exists and the quality value of the base immediately after ci otherwise. Seven average quality values are computed for the column: five for substitution, one for deletion, and one for insertion. Each of the five values for substitution corresponds to one of the five base types. Let qs(d) denote the average quality value for substitution involving base type d of the read, let qd denote the average quality value for deletion, and let qn denote the average quality value for insertion. The values are defined by the following formulas, where d is a regular base.
 |
 |
 |
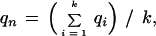 |
 |
Note that the quality values of the gap symbols in the column are excluded from the calculation of the average quality value for deletion. Any substitution involving base N is considered as a mismatch.
It should be pointed out that the current definition of the average quality values assumes that errors in overlapping reads occur independently. This assumption is not true in practice because the same error is likely to occur in the same local context, and overlapping reads contain many identical local contexts. A refined definition can be developed by using read type to address the dependence of errors, as suggested by one referee. In this definition, the quality values in a sum are partitioned into groups by sequencing chemistry and orientation, the quality values in each group are sorted in descending order, and the quality values in each group are given decreasing weights, respectively. For example, the largest value in the group is given a weight of 1.0, the second largest value a weight of 0.5, and so on. We plan to work out a set of decreasing weights for the group in the future.
The scores of a substitution, a deletion, and an insertion are defined as follows. Consider a substitution involving the column of the block and a base d of the read with quality value qr. If qs(d) > 0, then the substitution is considered as a match and its score is m * min[qs(d),qr], where the positive integer m is a match score factor. If qs(d) ≤ 0, then the substitution is considered as a mismatch and its score is n * min[−qs(d),qr], where the negative integer n is a mismatch score factor.
The score of a gap is the gap open score plus the gap extension score of each element in the gap. For simplicity, the gap open score is a small negative number independent of quality values. However, the extension score depends on quality values. Let a positive number g be a gap extension penalty factor. The extension score of a column with average deletion quality value qd in a deletion gap is −g * min(qd,qr), where qr is the quality value of a base of the read immediately before or after the gap. The extension score of a base of the read with quality value qr in an insertion gap is −g * min(qn,qr), where qn is the average insertion quality value of a column of the block immediately before or after the gap. An example for calculation of scores of a match, a mismatch, a deletion, and an insertion is given in Figure 5.
Figure 5.

An example for calculation of scores of a match, a mismatch, a deletion, and an insertion. The quality values of bases are shown next to the bases. In each case, the average quality value of the column and the score are presented, where positive integer m is the match score factor, negative integer n is the mismatch score factor, and positive integer g is the gap extension penalty factor.
A global alignment of the block and the read with the maximum score is computed in linear space using a divide–conquer technique (Hirschberg 1975; Myers and Miller 1988; Huang 1994). Because the pairwise alignment computation is performed at most once for each read, it is affordable to carry out the computation over the entire dynamic programming matrix for best results. The average quality values for the block are precomputed so that each entry in the dynamic programming matrix is calculated in a constant time.
RESULTS
The methods discussed in the previous section have been implemented in the CAP3 program. Most of the 6700 lines of CAP3 code were newly written. CAP3 takes as input a file of sequence reads in FASTA format and two optional files: a file of quality values in FASTA format and a file of forward–reverse constraints. The file of quality values must be named xyz.qual, and the file of forward–reverse constraints must be named xyz.con, where xyz is the name of the sequence file. Each line of the constraint file specifies one forward–reverse constraint of the form ReadA ReadB MinDistance MaxDistance where ReadA and ReadB are the names of two reads, and MinDistance and MaxDistance are the lower and upper limits of a distance range. Assembly results in CAP format go to the standard output and need to be directed to a file. CAP3 also produces assembly results in ace file format (.ace). This step allows CAP3 output to be viewed in CONSED (Gordon et al. 1998). CAP3 reports the status of each constraint in a separate file. CAP3 produces a number of other output files as PHRAP. A version of CAP3 was developed by Kathryn Beal for use in the GAP4 program of the Staden package.
The CAP3 program was developed and tuned on real data sets and artificial data sets generated by GenFrag (Engle and Burks 1993). Those data sets were helpful in the identification of problems with the program. Below, we present results of CAP3 on four real BAC data sets. Although the program is under steady refinement, no change or tuning was made to the program on any of the four data sets.
Information on the four data sets is shown in Table 1. All the data sets contain full-length reads with low-quality regions and masked vector regions. Each data set contains a file of reads and a file of quality values produced by PHRED. Each data set was provided with a consensus sequence. For each data set, a file of forward–reverse constraints was produced by a program named Formcon from the file of reads according to the naming convention. The default values were used for all the parameters of CAP3. All tests were performed on a Sun Ultra 1 workstation.
Table 1.
BAC Data Sets
Assembly results by CAP3 on the four data sets are presented in Table 2. For each data set, the consensus sequence produced by CAP3 was aligned by a program named Check with the provided consensus sequence. The number of differences between the CAP3 consensus sequence and the provided consensus sequence was computed.
Table 2.
Results of CAP3 on BAC Data Sets
| Data set | Running time (min) | No. of large contigs | Length of CAP3 sequence | No. of differencesa |
|---|---|---|---|---|
| 203 | 37 | 1 | 90,292 | 0 |
| 216 | 154 | 1 | 132,057 | 17 |
| 322F16 | 127 | 1 | 157,982 | 11 |
| 526N18 | 73 | 2 | 180,128b | 10 |
The number of differences in highly similar regions of the CAP3 sequence and the provided sequence.
The sum of the lengths of two large contigs produced by CAP3.
CAP3 produced one large contig of 90,292 bp on data set 203. The region of the CAP3 sequence from base 516 to 90,292 (last base) is identical to the region of the provided sequence from base 1 to 89,777. The provided sequence contains two extra bases at the 3′ end because CAP3 trimmed the two bases off its consensus sequence. The CAP3 sequence is 515 bp longer than the provided sequence at the 5′ end. The 515-bp region contains a 144-bp low-quality end region. The 515-bp region in the CAP3 sequence is the consensus sequence of 3′ end regions of 5 reads in forward orientation. This suggests that the extra 515-bp region was probably removed from the provided sequence. CAP3 made no corrections using constraints.
CAP3 produced one large contig of 132,057 bp on data set 216. The region of the CAP3 sequence from base 14 to 120,934 is highly similar to the region of the provided sequence from base 3729 to 124,645 (last base). In other words, the CAP3 sequence and the provided sequence have an overlap of about 120,920 bp. The 3728-bp 5′ end region of the provided sequence is identical to the region of the CAP3 sequence from base 127,869 to 131,596. Both end regions (base 14–1828 and base 130,859–131,814) of the CAP3 sequence are Alu sequences. Because of these Alu sequences, the 3728-bp 5′ end region of the provided sequence was put by CAP3 at a different place. The 6934-bp region of the CAP3 sequence from base 120,935 to 127,868 is not similar to any part of the provided sequence. Because the original assembly is not available, it is not clear whether the 6934-bp region of the CAP3 sequence was removed from the provided sequence or was in a separate contig in the original assembly. CAP3 made one correction using constraints. The correction is supported by 11 constraints.
A total of 17 base differences were found in the 120,920-bp overlapping region between the CAP3 sequence and the provided sequence. The CAP3 alignment was examined at the positions of the 17 differences. Of the 17 differences, 7 occur in regions covered by one or two reads, 1 appears to be an error in the provided sequence, and 9 are errors in the CAP3 sequence due to stacking of two highly similar Alu copies in a 5′ end region of 550 bp.
CAP3 took much more time on data set 216 than on set 203 because CAP3 computed a larger number of overlaps on set 216. The number of overlaps for set 216 is about 6 times that for set 203. In general, an increase in CAP3 running time is mainly due to an increase in the number of overlaps computed by CAP3.
On data set 322F16, CAP3 produced one large contig of 157,982 bp. The region of the CAP3 sequence from base 22 to 157,982 (last base) is highly similar to the region of the provided sequence from base 1218 to 159,179 (last base). The 21-bp 5′ end region of the CAP3 sequence is the consensus sequence of 5′ end regions of three oligonucleotide reads in reverse orientation. The CAP3 sequence has no region similar to the 1217-bp 5′ end of the provided sequence because CAP3 missed a short overlap of 42 bp between a short contig of 1160 bp and the large contig of 157,982 bp.
A total of 11 differences were found in the highly similar regions of the CAP3 sequence and the provided sequence. Of the 11 differences, 2 are errors in the CAP3 sequence, 4 are errors in the provided sequence, and 5 are not clear as they occur in a region of low coverage. CAP3 made two corrections using constraints. One correction is supported by 10 constraints and the other by 9 constraints.
On data set 526N18, CAP3 produced two large contigs of 27,875 bp and 152,253 bp, respectively. CAP3 failed to use a weak overlap of 124 bp between the two contigs, which has a percent identity of 84%. However, CAP3 did report that the 3′ end of the 152,253-bp contig and the 5′ end of the 27,875-bp contig are linked by five constraints. The entire 152,253-bp CAP3 sequence is almost identical to the region of the provided sequence from base 78 to 152,332. The 77-bp 5′ end region of the provided sequence is from a 5′ end region of one read in the forward orientation. This region was removed by CAP3 from its consensus sequence. The almost identical regions contain four base differences: one is an error in the provided sequence, and three are not clear because of lack of consensus.
The entire 27,875-bp CAP3 sequence is highly similar to the region of the provided sequence from base 152,309 to 180,182 (last base). The highly similar regions contain six base differences: one is an error in the CAP3 sequence, and five are not clear because of lack of consensus, which occur at bases of quality values less than 10. All the six differences occur in an initial 66-bp region of the CAP3 sequence. CAP3 made one correction using constraints. The correction is supported by 14 constraints.
Comparison of CAP3 and PHRAP
CAP3 and PHRAP were compared on two types of data: low-pass data with forward–reverse constraints and data of various coverage without forward–reverse constraints. The evaluation goal for the low-pass data (of fivefold coverage) was to determine whether it was possible to construct scaffolds with CAP3 and PHRAP. The evaluation goal for the second type of data was to assess the performance of CAP3 and PHRAP in terms of the number and accuracy of contigs.
The low-pass data consist of seven BAC data sets (shown in Table 3). Forward–reverse constraints were obtained by sequencing both ends of every plasmid subclone. We were able to construct scaffolds with CAP3 in all of the seven BACs and with PHRAP in six of them. Because CAP3 produces a partial order of contigs by constraints, it was easier and faster to construct scaffolds with CAP3. The accuracy of each scaffold was checked by comparing the scaffolded sequence against the answer sequence. The details of this experiment will be published elsewhere.
Table 3.
Ability to Construct Scaffolds with CAP3 and PHRAP
| Data set | Length of answer sequence | No. of reads per kb | Ability to make scaffold with CAP3 | Ability to make scaffold with PHRAP |
|---|---|---|---|---|
| 188A7 | 112,773 | 10.6 | yes | yes |
| 201G24 | 184,666 | 10.8 | yes | yes |
| 213L3 | 135,545 | 10.3 | yes | yes |
| 257P13 | 184,998 | 10.1 | yes | yes |
| 488C13 | 187,237 | 11.1 | yes | yes |
| 501I4 | 231,464 | 11.7 | yes | no |
| 526N18 | 180,104 | 12.2 | yes | yes |
Shiaw-Pyng Yang at the Genome Sequencing Center, Washington University, evaluated the performance of CAP3 and PHRAP on a number of data sets with various depths of coverage (S.-P. Yang, pers. comm.). Those data sets were randomly generated for a desired depth of coverage from a real data set named H_NH0018C09. The real data set was produced on new capillary machines. PHRED was used to generate quality values for all reads. The latest version of PHRAP, the 3/19/99 version, was used in the evaluation. No forward–reverse constraints were used.
Four depths of coverage, 3, 5, 8, and 10, were selected. For each depth of coverage, four data sets were generated randomly by selection of reads from the real data set. CAP3 and PHRAP were run on each of the 16 data sets, and the consensus sequences produced by CAP3 and PHRAP were compared with the answer sequence of 167,358 bp. CAP3 and PHRAP performance data are shown in Table 4. On those data sets, PHRAP often produced longer contigs than CAP3, while CAP3 often produced fewer internal errors in consensus sequences than PHRAP. The CAP3 consensus sequences contain more errors than the PHRAP sequences within 500 bases of sequence ends. The reason for this result is that the 5′ and 3′ ends of each CAP3 consensus sequence were an end region of a raw read, which contains a large number of errors. The problem has been fixed by trimming the raw end region.
Table 4.
Performance of CAP3 and PHRAP
| Program | Data seta | Length of longest contig | No. of large contigs | Total length of gaps | Total no. of internal errorsb |
|---|---|---|---|---|---|
| CAP3 | 3XA | 6189 | 57 | 52,885 | 443 |
| PHRAP | 3XA | 6396 | 54 | 38,146 | 529 |
| CAP3 | 3XB | 12,368 | 44 | 71,761 | 71 |
| PHRAP | 3XB | 13,116 | 47 | 60,436 | 228 |
| CAP3 | 3XC | 10,709 | 49 | 54,229 | 227 |
| PHRAP | 3XC | 11,406 | 45 | 34,727 | 332 |
| CAP3 | 3XD | 11,408 | 43 | 67,586 | 115 |
| PHRAP | 3XD | 11,350 | 49 | 60,312 | 240 |
| CAP3 | 5XA | 10,582 | 42 | 27,965 | 249 |
| PHRAP | 5XA | 18,268 | 31 | 14,396 | 252 |
| CAP3 | 5XB | 26,034 | 17 | 10,405 | 100 |
| PHRAP | 5XB | 33,693 | 18 | 7,322 | 115 |
| CAP3 | 5XC | 20,939 | 29 | 20,520 | 172 |
| PHRAP | 5XC | 20,912 | 27 | 16,617 | 261 |
| CAP3 | 5XD | 14,219 | 35 | 23,635 | 46 |
| PHRAP | 5XD | 14,696 | 33 | 17,113 | 129 |
| CAP3 | 8XA | 71,025 | 12 | 4,681 | 83 |
| PHRAP | 8XA | 71,395 | 8 | 1,061 | 80 |
| CAP3 | 8XB | 53,127 | 8 | 883 | 59 |
| PHRAP | 8XB | 53,078 | 7 | 542 | 36 |
| CAP3 | 8XC | 52,134 | 8 | 752 | 4 |
| PHRAP | 8XC | 76,922 | 6 | 774 | 6 |
| CAP3 | 8XD | 72,690 | 7 | 1,241 | 35 |
| PHRAP | 8XD | 102,523 | 6 | 648 | 60 |
| CAP3 | 10XA | 91,380 | 4 | 0 | 28 |
| PHRAP | 10XA | 91,329 | 3 | 0 | 11 |
| CAP3 | 10XB | 167,655 | 1 | 0 | 5 |
| PHRAP | 10XB | 138,551 | 2 | 0 | 7 |
| CAP3 | 10XC | 106,631 | 5 | 321 | 44 |
| PHRAP | 10XC | 77,747 | 4 | 330 | 12 |
| CAP3 | 10XD | 79,900 | 4 | 468 | 2 |
| PHRAP | 10XD | 79,978 | 3 | 346 | 2 |
The number in the name of a data set is the estimated depth of coverage for the data set.
An error in a consensus sequence is internal if it is not within 500 bases of either sequence end.
DISCUSSION
We have introduced a number of new features in the CAP3 sequence assembly program. The features include fast identification of pairs of reads with an overlap, clipping of 5′ and 3′ poor regions of reads, efficient computation and evaluation of overlaps, use of forward–reverse constraints to correct errors in construction of contigs, and generation of consensus sequences for contigs. These features allow CAP3 to take full-length reads and produce more accurate sequences than CAP2.
An unusual feature of CAP3 is the algorithm for making use of constraints to correct assembly errors. The algorithm is very tolerant of errors in constraints. The algorithm makes a correction to the current assembly only if the correction is supported by a sufficient number of constraints. The random distribution of subclones implies that errors in constraints are also randomly distributed. Thus, it is very unlikely that a sufficient number of wrong constraints all consistently support a correction to the same region. The experimental results indicate that CAP3 is able to make corrections to contigs using constraints.
Because DNA sequence assembly is a difficult problem, it is beneficial to the genome sequencing community to develop several sequence assembly programs. These programs complement one another because they use different approaches. CAP3 differs from the other assembly programs in use of constraints to construct contigs and use of quality values to construct multiple sequence alignments. Below, we compare the CAP3 and PHRAP approaches to generation of consensus sequences for contigs.
CAP3 uses a multiple sequence alignment method to generate a consensus sequence for a contig. The multiple sequence alignment method is extended to weight bases by their quality values. The accuracy of this approach depends on the performance of the multiple sequence alignment method. If the bases of overlapping reads in a contig are properly aligned, then it is likely that a consensus base occurs in each column of the alignment, and an accurate sequence is generated for the contig. On the other hand, if the bases of overlapping reads are improperly aligned, then it is likely that conflicting bases occur in some columns and an inaccurate sequence is generated for the contig. The multiple alignment method may still work in the situation where the contig has a high depth of coverage, but individual reads are not very accurate.
PHRAP uses a different approach to generate a sequence for a contig. The sequence is a mosaic of read regions of the highest quality values. The mosaic approach does not make as full use of redundant coverage as the multiple alignment approach, nor does it have the problem of misaligning multiple bases that the multiple alignment approach occasionally does. The mosaic approach can work in the situation where the contig has a low depth of coverage, but each region of the contig is covered by a region of a read with high quality values.
Finally, we address the question of when to use CAP3 and PHRAP. If quality values are not available, then the user may choose CAP3 as CAP3 is able to use redundant coverage in construction of consensus sequences. The user may use CAP3 to make scaffolds on low-pass data with forward–reverse constraints as CAP3 uses forward–reverse constraints in assembly. Otherwise the user may select PHRAP. PHRAP often produces longer contigs than CAP3, whereas CAP3 often produces fewer errors in consensus sequences than PHRAP. If affordable, the user may use both CAP3 and PHRAP and compare their consensus sequences.
Availability
The CAP3 program is freely available for academic use at huang@mtu.edu. The CAP3 program can be used in the GAP4 program of the Staden Package (http://www.mrc-lmb.cam.ac.uk/pubseq). The CAP3 program can also be used together with the CONSED program. Additional information on CAP3 can be obtained at http://genome.cs.mtu.edu/sas.html.
Acknowledgments
We thank Kathryn Beal for incorporating CAP3 in GAP4, Rachel Dickhoff for help with low-pass data, Lee Hood and Rodger Staden for suggesting use of forward–reverse constraints, Jun Qian for producing CAP3 output in ace format, Bruce Roe, Lee Rowen, and Granger Sutton for discussions and data sets, Shiaw-Pyng Yang for comparing CAP3 and PHRAP, and the referees for constructive suggestions. This project was supported in part by National Institutes of Health grant R01 HG01502-03 from the National Human Genome Research Institute.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
E-MAIL huang@mtu.edu; FAX (906) 487-2283.
REFERENCES
- Altschul SF, Gish W, Miller W, Myers EW, Lipman DJ. Basic local alignment search tool. J Mol Biol. 1990;215:403–410. doi: 10.1016/S0022-2836(05)80360-2. [DOI] [PubMed] [Google Scholar]
- Bonfield JK, Smith K, Staden R. A new DNA sequence assembly program. Nucleic Acids Res. 1995;24:4992–4999. doi: 10.1093/nar/23.24.4992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chao K-M, Pearson WR, Miller W. Aligning two sequences within a specified diagonal band. Comput Appl Biosci. 1992;8:481–487. doi: 10.1093/bioinformatics/8.5.481. [DOI] [PubMed] [Google Scholar]
- Engle ML, Burks C. Artificially generated data sets for testing DNA fragment assembly algorithms. Genomics. 1993;16:286–288. doi: 10.1006/geno.1993.1180. [DOI] [PubMed] [Google Scholar]
- Ewing B, Green P. Base-calling of automated sequencer traces using Phred. II. Error probabilities. Genome Res. 1998;8:186–194. [PubMed] [Google Scholar]
- Ewing B, Hillier L, Wendl MC, Green P. Base-calling of automated sequencer traces using Phred. I. Accuracy assessment. Genome Res. 1998;8:175–185. doi: 10.1101/gr.8.3.175. [DOI] [PubMed] [Google Scholar]
- Gleizes A, Henaut A. A global approach for contig construction. Comput Appl Biosci. 1994;10:401–408. doi: 10.1093/bioinformatics/10.4.401. [DOI] [PubMed] [Google Scholar]
- Gordon D, Abajian C, Green P. Consed: A graphical tool for sequence finishing. Genome Res. 1998;8:195–202. doi: 10.1101/gr.8.3.195. [DOI] [PubMed] [Google Scholar]
- Green, P. 1996. http://bozeman.mbt.washington.edu/phrap.docs/phrap.html.
- Hirschberg DS. A linear space algorithm for computing maximal common subsequences. Commun Assoc Comput Mach. 1975;18:341–343. [Google Scholar]
- Huang X. A contig assembly program based on sensitive detection of fragment overlaps. Genomics. 1992;14:18–25. doi: 10.1016/s0888-7543(05)80277-0. [DOI] [PubMed] [Google Scholar]
- ————— On global sequence alignment. Comput Appl Biosci. 1994;10:227–235. doi: 10.1093/bioinformatics/10.3.227. [DOI] [PubMed] [Google Scholar]
- ————— An improved sequence assembly program. Genomics. 1996a;33:21–31. doi: 10.1006/geno.1996.0155. [DOI] [PubMed] [Google Scholar]
- ————— Fast comparison of a DNA sequence with a protein sequence database. Microb Comp Genomics. 1996b;1:281–291. doi: 10.1089/mcg.1996.1.281. [DOI] [PubMed] [Google Scholar]
- Kececioglu J D, Myers EW. Combinatorial algorithms for DNA sequence assembly. Algorithmica. 1995;13:7–51. [Google Scholar]
- Larson S, Jain M, Anson E, Myers EW. “An interface for a fragment assembly kernel.” Technical report TR 96-04A. Tucson, AZ: Department of Computer Science, The University of Arizona; 1996. [Google Scholar]
- Lawrence CB, Honda S, Parrott NW, Flood TC, Gu L, Zhang L, Jain M, Larson S, Myers EW. The genome reconstruction manager: A software environment for supporting high-throughput DNA sequencing. Genomics. 1994;23:192–201. doi: 10.1006/geno.1994.1477. [DOI] [PubMed] [Google Scholar]
- Myers EW, Miller W. Optimal alignments in linear space. Comput Applic Biosci. 1988;4:11–17. doi: 10.1093/bioinformatics/4.1.11. [DOI] [PubMed] [Google Scholar]
- Pearson WR, Lipman D. Improved tools for biological sequence comparison. Proc Natl Acad Sci. 1988;85:2444–2448. doi: 10.1073/pnas.85.8.2444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peltola H, Soderlund H, Ukkonen E. SEQAID: A DNA sequence assembling program based on a mathematical model. Nucleic Acids Res. 1984;12:307–321. doi: 10.1093/nar/12.1part1.307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith TF, Waterman MS. Identification of common molecular subsequences. J Mol Biol. 1981;147:195–197. doi: 10.1016/0022-2836(81)90087-5. [DOI] [PubMed] [Google Scholar]
- Smith S, Welch W, Jakimciu A, Dahlberg T, Preston E, Van Dyke D. High throughput DNA sequencing using an automated electrophoresis analysis system and a novel sequence assembly program. Biotechniques. 1993;14:1014–1018. [PubMed] [Google Scholar]
- Staden R. A new computer method for the storage and manipulation of DNA gel reading data. Nucleic Acids Res. 1980;8:3673–3694. doi: 10.1093/nar/8.16.3673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton GG, White O, Adams MD, Kerlavage AR. TIGR assembler: A new tool for assembling large shotgun sequencing projects. Genome Sci Technol. 1995;1:9–19. [Google Scholar]