Regla Pýþagórasar
Regla Pýþagórasar,[1][2] Pýþagórasarregla[3] eða setning Pýþagórasar[3] er regla í evklíðskri rúmfræði sem fjallar um tengslin milli lengda hliða í rétthyrndum þríhyrningi. Reglan er kennd við forngríska heimspekinginn, trúarleiðtogann og stærðfræðinginn Pýþagóras, þó að vitað sé að reglan hafi þekkst fyrir tíma hans bæði í Babýlóníu og Kína, en talið er að hann hafi verið fyrstur til að sanna að hún gilti fyrir alla rétthyrnda þríhyrninga.
Reglan er grundvallarregla í ýmsum rúmfræðireikningi, t.a.m. hnitarúmfræði og hornafræði.
Reglan
[breyta | breyta frumkóða]
Setningin segir að í rétthyrndum þríhyrning er summa ferninga skammhliðanna jöfn ferningnum á langhliðina.
Ef hliðarlengdir þríhyrningsins eru a, b, c, þar sem c er langhliðin, gildir því
.
Ef smíðaðir eru þrír ferningar, þar sem hver hinna þriggja hliða þríhyrningsins jafngildir hliðarlengd eins fernings, er samanlagt flatarmál minni ferninganna tveggja jafnt flatarmáli þess stærsta.
Sönnun
[breyta | breyta frumkóða]Til eru fjölmargar mismunandi sannanir á reglu Pýþagórasar[4]. Eftirfarandi sönnun byggir á reglu um einslaga þríhyrninga.
Látum þríhyringinn ABC vera þannig að hornið C er rétt. Drögum línuna CX hornrétt á hliðina AB. Þá myndast tveir nýir þríhyrningar, ACX og CBX. Þessir þríhyrningar eru báðir einslaga þríhyrningnum ABC.
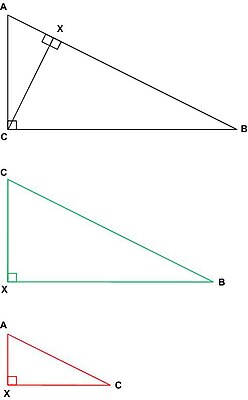
Þar sem er , og þar sem er .
Því fæstÞar sem fáum við að
.
Skrifum , svo að
eins og sanna átti.
Tengt efni
[breyta | breyta frumkóða]
Tilvísanir
[breyta | breyta frumkóða]- ↑ „Hvernig er regla Pýþagórasar sönnuð?“. Vísindavefurinn.
- ↑ Regla Pýþagórasar á Rasmus
- ↑ 3,0 3,1 „theorem of Pythagoras“. Afrit af upprunalegu geymt þann 5. mars 2016. Sótt 25. maí 2011.
- ↑ „Pythagorean Theorem and its many proofs“. www.cut-the-knot.org. Sótt 14. ágúst 2023.