Abstract
Recent developments in RNA-sequencing (RNA-seq) technology have led to a rapid increase in gene expression data in the form of counts. RNA-seq can be used for a variety of applications, however, identifying differential expression (DE) remains a key task in functional genomics. There have been a number of statistical methods for DE detection for RNA-seq data. One common feature of several leading methods is the use of the negative binomial (Gamma–Poisson mixture) model. That is, the unobserved gene expression is modeled by a gamma random variable and, given the expression, the sequencing read counts are modeled as Poisson. The distinct feature in various methods is how the variance, or dispersion, in the Gamma distribution is modeled and estimated. We evaluate several large public RNA-seq datasets and find that the estimated dispersion in existing methods does not adequately capture the heterogeneity of biological variance among samples. We present a new empirical Bayes shrinkage estimate of the dispersion parameters and demonstrate improved DE detection.
Keywords: Differential expression, Empirical Bayes, RNA sequencing, Shrinkage estimator
1. Introduction
The recent developments in RNA-sequencing (RNA-seq) technology have led to a rapid increase in gene expression data in the form of counts. RNA-seq enables some applications not achievable by microarrays, including discovering novel transcripts and alternative splicing. One fundamental question in functional genomics, however, remains the regulation of gene expression under the different conditions (treatments, genotypes, environments, or developmental stages). Therefore, identifying differential expression (DE) is still a key task in transcriptomics research.
The measurement of expression in RNA-seq is the number of sequenced fragments that can be mapped to a genomic unit of interest, which can be a gene, an exon, or any region of interest. We use gene thereafter for convenience. One major difference in the DE detection methods for RNA-seq and microarray data is that data from microarrays are often modeled as a Gaussian distribution after proper preprocessing. These methods do not take into account the discrete nature of RNA-seq data and thus may not be directly applicable. There are nonetheless some common features between the two technologies. For example, the advancement in technology does not eliminate biological variability, which early applications of RNA-seq often neglected(Hansen and others, 2011). In fact, the much higher dynamic range of RNA-Seq data makes the heteroskedasticity, i.e. the gene-specific dispersion, even more important than it was with microarrays.
In both types of gene expression data, there are two sources of variation: technical variation, which represents the measurement error inherent to the technology and sample preparation, and biological variation, which represents the heterogeneity among samples in the same treatment group or population. If all subjects within the same group have an identical expression level for a given gene, i.e. lacking biological variation, the counts for that gene can be modeled as a Poisson random variable, as done byMarioni and others (2008) and Wang and others (2010). The earliest tests for DE essentially tested for whether the difference of average counts in two groups exceeds what is expected by Poisson sampling error. However, since gene expression is a stochastic process, biological replicates in the same treatment group do not share identical expression levels. The presence of biological variation leads to the “over-dispersion” problem, e.g. the read counts show variation greater than expected from Poisson random variables.
A common approach to address the over-dispersion problem is to use the negative binomial (NB) model. The NB model is a Gamma–Poisson mixture and can be interpreted as the following: the Gamma distribution models the unobserved true expression levels in each biological sample, and conditioning on the expression level, the measurement from the sequencing machine follows a Poisson distribution(Robinson and Smyth, 2007; Anders and Huber, 2010; Hardcastle and Kelly, 2010). The variance from an NB distribution depends on the mean μ in the relationship:
 |
(1.1) |
where the first term represents variance due to Poisson sampling error and the second term represents variance due to variation between biological replicates. The parameter ϕ is referred to as the dispersion parameter. Note that ϕ is the reciprocal of the shape parameter in the Gamma distribution, and thus is the squared coefficient of variation (CV). Therefore, ϕ represents the variation of a gene’s expression relative to its mean.
Most statisticians agree that the over-dispersion problem needs to be addressed. The difference is how the dispersion is modeled, estimated, and used in inference.Robinson and Smyth (2008) assume a common dispersion for all genes and use information from all genes to estimate a global ϕ. This stabilizes the estimation for ϕ but a common dispersion means an identical CV for all genes, while it is known that some genes are more tightly controlled (e.g. housekeeping genes) and other genes vary much more relative to their means (e.g. immune-modulated and stress-induced genes(Pritchard and others, 2001)). The gene-specific biological variation is reproducible across technologies(Hansen and others, 2011) and is not reflected by a common dispersion. As a result, genes that are naturally more variable are more likely to be reported as DE due to an underestimation of their dispersion.Anders and Huber (2010) introduce DESeq, another method based on the NB model. Instead of assuming the second term in(1.1) to be proportional to μ2 with a dispersion ϕ, they let the variance be a smooth function of the mean (with proper offset accounting for the sequencing depth). However, the model inAnders and Huber (2010) still assumes that conditioning on the mean expression, the variance is constant. That is, two genes with the same mean expression level also has the same variance. There have been many updates of the DESeq package and the current version uses the greater value between the empirical gene-specific dispersion and the mean-dependent fitted value. Robinson and Smyth (2007) modify the common dispersion model and introduce an empirical Bayes shrinkage estimate using weighted conditional log-likelihood. This new estimate shrinks the sample dispersion for each gene toward a common prior instead of shrinking them completely to the common dispersion. The method is implemented in the widely used R/Bioconductor package edgeR(Robinson and others, 2010), with recent extensions to multifactor experiments(McCarthy and others, 2012). Hardcastle and Kelly (2010) use NB distribution for the counts in a Bayesian hierarchical model setting. Non-parametric prior distributions for the NB parameters are empirically determined. This is a much more computationally intensive method and, possibly for this reason, not as widely applied as edgeR and DESeq.
Since these publications, many RNA-seq studies have emerged and the accumulated RNA-seq datasets with a reasonable number of replicates encourage us to re-evaluate the estimation of dispersion in RNA-seq. We find that existing methods often capture the overall level of dispersion but do not adequately reflect the heterogeneity in dispersion among genes. In this paper, we propose a new empirical Bayes method to shrink the dispersion parameter. We demonstrate using real data-based simulation that the proposed method provides a better estimate for the gene-specific dispersion and improves DE detection. The rest of the paper is organized as follows. In Section2, we describe the datasets that provide both the motivation for this research and the basis for the evaluation of DE detection. In Section3, we demonstrate the limitation of current estimation of the dispersion parameter and motivate our model for the prior distribution of the dispersion parameter. In Section4, we present the hierarchical model, estimation, and testing procedure. In Section5, we compare the DE detection using the proposed method with the leading alternatives. Finally,in Section6, we discuss the interpretation of the dispersion, the connection with microarray data, and future directions.
2. Data description
Two real RNA-seq datasets are used in the paper for estimating simulations parameters and showing motivational plots. The first is fromCheung and others (2010), which quantifies the expressions of lymphoblastoid cell lines from 41 CEU individuals in International HapMap Project(Gibbs and others, 2003). The second is from Blekhman and others (2010), which includes six liver samples from both males and females. These datasets are referred to as “Cheung data” and “Gilad data”, respectively, thereafter. For both datasets, the sequence reads are summarized into counts within genes from Ensembl 61 annotation. The gene counts are obtained from the ReCount webpage presented byFrazee and others (2011). Samples in both datasets include biological replicates, so the variance in observed data is a result of both biological variation and technical variation.
We also use data from the MicroArray Quality Control Project (MAQC)(Shi and others, 2006) phase III, also known as Sequencing Quality Control. Two biological samples, human brain and universal human reference sample, are assayed using seven lanes each. The MAQC data use samples from the same library preparation protocols, and thus represent data with technical replicates only. This dataset provides an extreme case in which the biological variation reaches the lower bound.
3. Motivation
The NB distribution is widely used in modeling sequence count data because the Gamma–Poisson mixture provides a natural hierarchy for the generation of sequencing counts. The Gamma distribution is a flexible continuous distribution that characterizes the expression rate for a gene. Given the expression rate in a biological sample, the sequencing technology provides a count from a Poisson process with the mean proportional to the expression rate and an offset related to sequencing depth and possibly other factors affecting the detection efficiency (Hansen and others, 2012). When there are a large number of replicates, the dispersion parameter can be estimated from the data and over-dispersion is a well-addressed problem in the generalized linear model framework. The challenge in RNA-seq data is that there are often very limited replicates, such that the sample estimate of gene-specific dispersion is unstable. In this case, it is often useful to combine information from other genes to improve the estimation. DESeq and edgeR are the most widely used methods that provide shrinkage estimates of the dispersions by borrowing information across genes. To assess how well the dispersions are estimated from these methods, we conduct a simulation based on real data. First the gene-specific means and dispersions are estimated from the Cheung data. Pseudo-datasets of 20 000 genes, in two treatment groups with four replicates each, are constructed under the NB model with parameters taken from the real data. The mean expressions are directly sampled from estimated gene-specific means non-parametrically. The dispersions are generated from log-normal(−1.72,1.072), which well approximates the empirical distribution of the dispersion observed in the Cheung data (supplementary material available at Biostatistics online, Figure S1).
DESeq function estimateDispersions with the default settings (sharing Mode="maximum" and fitType="parametric") and edgeR functions estimateCommon Disp followed by estimateTagwiseDisp with the default settings (trend="movingave", prop.used=0.3, method="grid") are applied to the simulated counts to obtain estimated dispersions. Figure1(a) and(b) shows the estimated versus true dispersions from both methods. Clearly, the estimates do not correlate well with the truth. Although both edgeR and DESeq estimate the central magnitude of the dispersions well, they fail to capture the variations in dispersions among genes. Changing the settings in the edgeR function estimateTagwiseDisp leads to different estimates (supplementary material available at Biostatistics online, Figure S4), but does not appear to substantially increase the accuracy of the estimated dispersion. The near horizontal clusters of points show that the dispersion of many genes are estimated to be approximately the same, which indicates over-shrinkage of the dispersions.
Fig. 1.

Estimated versus true dispersion from (a) edgeR, (b) DESeq and (c) DSS, based on simulation. Simulated data were generated for 20 000 genes and two treatment groups with four replicates in each group. The dispersions were randomly simulated from log-normal distribution with mean −1.72 and standard deviation 1.07, which match those parameters observed from the Cheung data. Different colors represent genes with different levels of average read counts. A figure showing the genes in different color strata in separate panels is included as supplementary material available at Biostatistics online, Figure S2.
Since the dispersion parameter represents biological variation, having a good estimate of ϕ is crucial to finding the DE that is beyond natural biological variation. In order to account for gene-specific dispersion, we take advantage of real RNA-seq datasets with replicates and note that the distribution of the logarithm of sample dispersion,  , is approximately Gaussian as shown in Figure2. In the next section, we describe a novel shrinkage estimator for ϕ using a log-normal prior and an NB likelihood. In Section5, we show that the proposed method greatly improves the estimation of ϕ and leads to better detection of the DE.
, is approximately Gaussian as shown in Figure2. In the next section, we describe a novel shrinkage estimator for ϕ using a log-normal prior and an NB likelihood. In Section5, we show that the proposed method greatly improves the estimation of ϕ and leads to better detection of the DE.
Fig. 2.
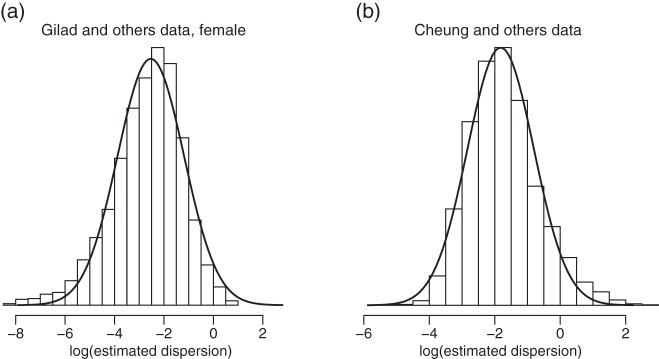
Histogram for the logarithm of estimated gene-specific dispersions (ϕg) from (a) Gilad and (b) Cheung data. Only female samples are used for the Gilad data. The solid lines are density curves for normal distribution with parameters estimated from  . It can be seen that ϕg can be approximately modeled as a log-normal distribution.
. It can be seen that ϕg can be approximately modeled as a log-normal distribution.
4. Methods
Denote the observed counts from gene g in sample i by Y gi, and the unobserved expression rate by θgi. We assume the following hierarchical model:
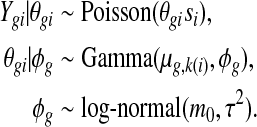 |
Here the Gamma distribution is parameterized with mean and dispersion (ϕg is the reciprocal of the shape parameter in the common parameterization); k(i) denotes the treatment group of sample i; and si represents the normalizing factor, such as the relative library size, for sample i. This normalization factor could also be a gene-specific factor, taking into account the varying sequencing efficiency due to the guanine-cytosine content and/or length (Hansen and others, 2012; Risso and others, 2012), but would nonetheless be treated as a known constant. Based on the hierarchical model, the marginal distribution of Y gi given μg,k(i) and ϕg is NB with mean νgi=μg,k(i)si and dispersion ϕg. In the simplest setting where there are only two groups, the goal of DE detection is to test, for each gene, whether the mean expressions are identical in both groups, e.g. μg,1=μg,2, as noted by other researchers(Robinson and Smyth, 2007, 2008; Anders and Huber, 2010; Robinson and others, 2010).
Estimating ϕg is a crucial step in DE detection and shrinkage estimators have been shown to be useful in typical RNA-seq experiments with a small number of replicates(Anders and Huber, 2010; Hardcastle and Kelly, 2010; Robinson and others, 2010). As discussed in previous works (Robinson and Smyth, 2007), there is no conjugate prior for ϕg to ease the computation of a posterior distribution. Thus, we decide to use a prior that approximates the ϕg in real RNA-seq data. We choose the log-normal distribution, motivated by Figure2.
For gene g, the conditional posterior distribution of ϕg given all observed counts and means, p(ϕg|Y gi,νgi,i=1,…,n) satisfies (detailed derivation can be found in supplementary material available at Biostatistics online):
 |
(4.1) |
where ψ(.) is the log gamma function and n is the number of samples. To obtain a point estimate of ϕg, we could compute the posterior mean by using numerical methods such as importance sampling. It is, however, too computationally intensive to be practical for RNA-seq data. Instead, we compute the posterior mode by maximizing an approximate of (4.1) and denote the estimate by 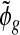 .
.
Specifically, we substitute νgi by 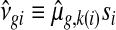 where
where  , and nk(i) is the number of samples in the same treatment group as i. The estimate
, and nk(i) is the number of samples in the same treatment group as i. The estimate  is the same as the sample estimate of true concentration in Anders and Huber (2010). We plug in the hyper-parameters m0,τ2 estimated from the data, and maximize the approximated Equation(4.1) using the Newton–Raphson method. In practice, we use “optimize” function in R , which provides excellent computational performance.
is the same as the sample estimate of true concentration in Anders and Huber (2010). We plug in the hyper-parameters m0,τ2 estimated from the data, and maximize the approximated Equation(4.1) using the Newton–Raphson method. In practice, we use “optimize” function in R , which provides excellent computational performance.
The hyper-parameters m0,τ2 are estimated from the data by pooling information from all genes (details in the next subsection). The estimate 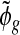 is therefore an empirical Bayes estimate shrunken toward the common prior. It can also be viewed as an estimate that maximizes a penalized pseudo-likelihood, as we are maximizing an approximate of the penalized likelihood (4.1), with penalty
is therefore an empirical Bayes estimate shrunken toward the common prior. It can also be viewed as an estimate that maximizes a penalized pseudo-likelihood, as we are maximizing an approximate of the penalized likelihood (4.1), with penalty  , by replacing the nuisance parameter νgi by its estimate
, by replacing the nuisance parameter νgi by its estimate  . The first term in the penalty,
. The first term in the penalty,  , penalizes values that deviate far from the common prior m0 and the second term adds an additional penalty for large values of ϕg. As mentioned in Section1, ϕg has the interpretation of the squared CV. Based on RNA-seq data from human populations(Cheung and others, 2010; Pickrell and others, 2010), we observe that around 70% of the genes have a CV less than 0.5. The CV in inbred animal models or established cell lines are likely even lower. Thus, penalizing larger ϕg appears a desirable feature.
, penalizes values that deviate far from the common prior m0 and the second term adds an additional penalty for large values of ϕg. As mentioned in Section1, ϕg has the interpretation of the squared CV. Based on RNA-seq data from human populations(Cheung and others, 2010; Pickrell and others, 2010), we observe that around 70% of the genes have a CV less than 0.5. The CV in inbred animal models or established cell lines are likely even lower. Thus, penalizing larger ϕg appears a desirable feature.
Estimating hyper-parameters. We start with a simple dispersion estimate for each gene motivated by the method of moments. Define a new random variable  ; we have
; we have  , which is identical for every sample in a certain treatment group. Using the sample mean to estimate the first moment of zgi and pooling data from different treatment groups together, one can obtain an estimator
, which is identical for every sample in a certain treatment group. Using the sample mean to estimate the first moment of zgi and pooling data from different treatment groups together, one can obtain an estimator  (detailed derivation in supplementary material available at Biostatistics online).
(detailed derivation in supplementary material available at Biostatistics online).
Next we estimate m0 and τ using the empirical distribution of  . We use the median of
. We use the median of  ’s,
’s,  , to estimate m0. The estimation of τ2 is less straightforward as the sample variance of
, to estimate m0. The estimation of τ2 is less straightforward as the sample variance of  overestimates τ2. The sample variance of
overestimates τ2. The sample variance of 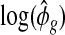 comprises two parts: τ2, the variance representing the heterogeneity of
comprises two parts: τ2, the variance representing the heterogeneity of  ’s among genes, and
’s among genes, and 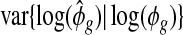 , the variation due to estimating
, the variation due to estimating  . Even when τ2=0 (all genes share common dispersion, ϕg=ϕ0∀g), we still observe non-zero
. Even when τ2=0 (all genes share common dispersion, ϕg=ϕ0∀g), we still observe non-zero 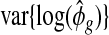 . Therefore, it is important to take into account this inflation in sample variance of
. Therefore, it is important to take into account this inflation in sample variance of 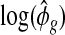 . We use an ad hoc adjustment that behaves well in practice evaluated by extensive simulation. Specifically, we create a pseudo-dataset with τ2=0 by simulating
. We use an ad hoc adjustment that behaves well in practice evaluated by extensive simulation. Specifically, we create a pseudo-dataset with τ2=0 by simulating 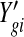 from
from  , where
, where  is used as common dispersion for all genes. We then compute the sample dispersion
is used as common dispersion for all genes. We then compute the sample dispersion  for each gene, and estimate
for each gene, and estimate 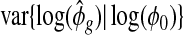 as
as 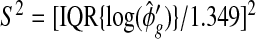 . From a number of pseudo-datasets, we obtain the mean
. From a number of pseudo-datasets, we obtain the mean 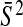 as the baseline. Lastly, we estimate τ2 as
as the baseline. Lastly, we estimate τ2 as  . Here c0 is the lower bound for
. Here c0 is the lower bound for  . In practice, we use c0=0.01.
. In practice, we use c0=0.01.
Note that 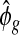 is only used in estimating the hyper-parameters and not directly used to obtain the shrinkage estimate
is only used in estimating the hyper-parameters and not directly used to obtain the shrinkage estimate  . Although each
. Although each  is a rather crude estimate of the dispersion, especially for a small number of samples, the large number of genes in RNA-seq data allows us to obtain stable estimates of the hyper-parameters. Once the prior is established in the empirical Bayesian method, our shrinkage estimate
is a rather crude estimate of the dispersion, especially for a small number of samples, the large number of genes in RNA-seq data allows us to obtain stable estimates of the hyper-parameters. Once the prior is established in the empirical Bayesian method, our shrinkage estimate  directly comes from maximizing(4.1).
directly comes from maximizing(4.1).
Test statistic and false discovery rate. With all parameters estimated, a hypothesis testing for the comparison of any two groups can be carried using a Wald test or exact test.Bullard and others (2010) show that the likelihood ratio test and the exact test perform similarly. Our simulation show that the exact test and the Wald test provide similar performance (supplementary material available at Biostatistics online, Figure S9). We choose to use the Wald test for its simplicity.
The Wald test statistic for two-group comparison is constructed as
 |
where  , is the estimated variance for
, is the estimated variance for  (detailed derivation in supplementary material available at Biostatistics online), and
(detailed derivation in supplementary material available at Biostatistics online), and 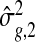 similarly defined. When there is no need for normalization (sj=1∀j),
similarly defined. When there is no need for normalization (sj=1∀j), 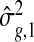 reduces to
reduces to 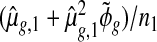 , an estimate of the variance in(1.1), standardized by the sample size in group 1.
, an estimate of the variance in(1.1), standardized by the sample size in group 1.
It is not trivial to derive the null distribution for the test statistic and the asymptotic distribution is irrelevant for most RNA-seq data. However, the empirical distribution of tg is Gaussian-like (Figure5(a)) and we can estimate a local false discovery rate (FDR) based on the empirical null (Efron, 2004) estimated from the data.
Fig. 5.

Statistical inferences from simulation. Dispersions used in simulations were generated from Gamma distributions with parameters estimated from Cheung data. (a) Quantile–Quantile normal plot for Wald statistics from DSS. (b) Reported and true FDR curves for top-ranked genes. Solid lines represent true FDRs. Dashed lines represent reported FDRs.
We implemented the proposed method in an R package titled “DSS”, standing for Dispersion Shrinkage for Sequencing. The package is available from Bioconductor.
5. Results
We compare results from the proposed method with two most widely used software packages, edgeR (version 2.6.2) and DESeq (version 1.8.2) using their latest release versions. For DESeq, we call the functions estimateDispersions and nbinomTest with default settings. For edgeR, we call functions estimateCommonDisp followed by estimateTagwiseDisp to estimate the dispersion parameter, and exactTest to test for DE.
First, we show an improvement in estimating the gene-specific dispersion parameter ϕg. All three methods use the common NB model, and estimating ϕg is the key challenge and what determines the ability to rank the truly DE genes above the null genes. In Figure1(c), we show the estimates  plotted against true ϕg. It is clear that the shrinkage estimates from DSS track the real dispersion much better than those from edgeR or DESeq. Note that the dispersion parameter estimates are shrunk more for genes with lower counts, as expected, since for those genes there is little information about ϕ in the data.
plotted against true ϕg. It is clear that the shrinkage estimates from DSS track the real dispersion much better than those from edgeR or DESeq. Note that the dispersion parameter estimates are shrunk more for genes with lower counts, as expected, since for those genes there is little information about ϕ in the data.
To quantify the improvement,we further use a similar approach as done inRobinson and Smyth (2007) to compare ϕg estimation. The mean squared error (MSE) of the estimates, in the scale of ϕg/(1+ϕg), were calculated from 50 simulations. Instead of using fixed mean expressions as inRobinson and Smyth (2007), we use a more realistic approach and randomly sample from mean expressions computed from the Cheung data. DSS has the lowest MSE in both settings (Figure3), and in all strata of mean expression (supplementary material available at Biostatistics online, Figure S3). We next compare the ability to detect the DE under a variety of situations. To evaluate DE detection under known truth, and to conduct the comparison under the most realistic scenario encountered in RNA-seq experiments, we simulated data semi-parametrically based on real RNA-seq datasets. In all simulations, the mean expressions were randomly sampled from the means calculated from the source dataset, Cheung or Gilad. The dispersion parameters were generated from parametric distributions, in which the parameters were computed from the source dataset (details in supplementary material available at Biostatistics online). To demonstrate robustness to distributional assumption, we simulated ϕg from both log-normal and Gamma distribution. In all simulations, 5% of all genes were true DE genes as this proportion is expected to be low in most gene expression experiments(Smyth, 2004). The logarithm of fold changes for the DE genes were randomly sampled from N(0,1).
Fig. 3.
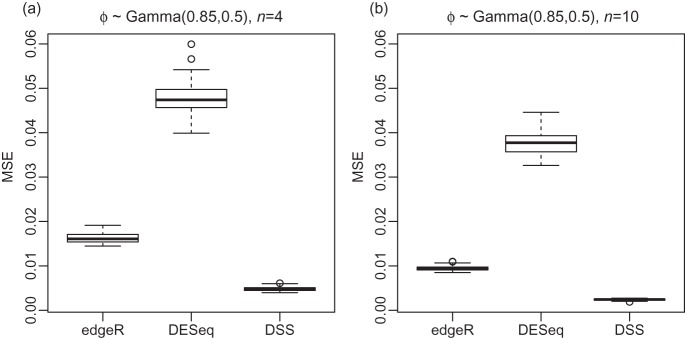
Boxplots comparing the distribution of MSE for dispersion estimations from edgeR, DESeq and DSS over 50 simulations. In all simulations, dispersions ϕg are randomly generated from Gamma distribution with shape 0.85 and scale 0.5. The mean expressions are randomly sampled from the means calculated from Cheung data. Simulations are performed under different sample sizes: (a) 4 replicates, and (b) 10 replicates. All simulations are for 2000 genes.
First, we evaluate the ability to rank true DE genes above non-DE genes. Since DE detection is often used as a hypothesis generating tool, and the goal is to have as many true positives as possible in the top-ranked genes, we compare the percentage of true DEs (i.e. 1−false discovery proportion) in the top-ranked genes up to top 1000. DSS shows a much higher proportion of true positives among the top-ranked genes when the dispersion is based on biological replicates as seen in the Gilad and Cheung data (Figure4). All three methods provide identical performances when the biological variations are near zero transcriptome wide, as expected in technical replicates such as MAQC data in supplementary material available at Biostatistics online, Figure S11.
Fig. 4.
DE detection accuracies from DSS, edgeR and DESeq for top 1000 ranked genes. Genes are ranked by the absolute Wald-statistic, from high to low, for DSS; ranked by p-values, from low to high, for edgeR and DESeq. The proportion of true discovery among top-ranked genes is plotted against the number of top-ranked genes. (a) The dispersion parameter simulated from log-normal distribution, with parameters estimated from the Gilad data. (b) The dispersion parameter simulated from log-normal distribution, with parameters estimated from the Cheung data. (c) The dispersion parameter simulated from Gamma distribution, with parameters estimated from the Gilad data. (d) The dispersion parameter simulated from Gamma distribution, with parameters estimated from the Cheung data.
To further evaluate the performance of DSS in ranking genes under different dispersion patterns, we performed additional simulations with dispersion from different distributions. We found that in general when the variation in dispersions is large, DSS provides better performance. The average dispersion level does not cause much differences among the results from the three methods. This is consistent with the findings that DESeq and edgeR provide reasonable estimates for the average dispersion, but underestimate the variations in dispersion due to over-shrinkage. The results for these simulations are presented in supplementary material available at Biostatistics online (Section10, Figures S6 and S7).
In addition to better sensitivity/specificity, another important task in DE detection is to provide a measure of statistical significance to guide the choice of a cut-off. In genomics, this is typically done using the FDR or some variant of the FDR. The Wald statistic in DSS is Gaussian-like in the center (Figure5(a)) and satisfies the assumption in local FDR calculation(Efron, 2004). Based on the connection between the local FDR and the FDR(Efron, 2004), we convert the local FDR to the scale of the classical FDR for comparison. For edgeR and DESeq, we use the FDR reported from the packages. Figure5(b) plots the reported (dashed lines) and true FDRs (solid lines) for the top-ranked genes from the simulation. The simulation settings are the same as those used in Figure4(b). The curves are averaged from 50 simulations. For DSS, the reported FDR curve is close to the true FDR. In contrast, both edgeR and DESeq give misleading FDR estimations. The underestimation of the FDR in the top-ranked genes gives an over-optimistic certainty in the reported DE. Supplementary material available at Biostatistics online, Figure S8, shows the comparison of the FDR under more simulation settings.
6. Discussion
We present a new shrinkage estimator for the dispersion parameter in the NB model for RNA-seq data. We show that this new estimator better captures the variation in gene-specific dispersion and, as a result, leads to a better detection in the DE compared with two most popular DE detection softwares DESeq and edgeR. In addition, the nominal FDR based on the local FDR method is much closer to the actual FDR. We do not include another method, baySeq, in the comparisons because the computational time becomes formidable for the large number of simulations we perform.
We find that a good estimate of ϕg is critical in DE detection when biological replicates are involved. This is not surprising as we have seen in the past decade that improving the estimation of the gene-specific variance in microarray data has greatly improved DE detection by using moderated Wald tests, including the most widely used methods LIMMA(Smyth, 2004) and SAM(Tusher and others, 2001). In fact, we find that ϕg has a similar interpretation as the gene-specific variance in microarray data. Let Y represent an untransformed expression level in microarray data. It is often assumed that  , where μ and σ2 are the mean and variance for the log scale expression measure, respectively. In the original scale, the squared CV CV (Y)2=eσ2−1≈σ2 for σ2≪1, which is satisfied in most genes (McCall and others, 2011). Thus, σ2 is approximately the squared CV in the untransformed scale. In comparison, RNA-seq data are often modeled by the NB distribution, i.e. a Gamma–Poisson mixture, in which the Gamma distribution models the biological variation and the Poisson distribution models the variation due to the counting process in sequencing. The dispersion parameter ϕg is the squared CV of the Gamma distribution, i.e. ϕg represents the gene-specific biological variation, and is directly linked to
, where μ and σ2 are the mean and variance for the log scale expression measure, respectively. In the original scale, the squared CV CV (Y)2=eσ2−1≈σ2 for σ2≪1, which is satisfied in most genes (McCall and others, 2011). Thus, σ2 is approximately the squared CV in the untransformed scale. In comparison, RNA-seq data are often modeled by the NB distribution, i.e. a Gamma–Poisson mixture, in which the Gamma distribution models the biological variation and the Poisson distribution models the variation due to the counting process in sequencing. The dispersion parameter ϕg is the squared CV of the Gamma distribution, i.e. ϕg represents the gene-specific biological variation, and is directly linked to 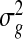 in log-transformed microarray expression data.
in log-transformed microarray expression data.
This interpretation explains several findings in our analysis of RNA-seq data with biological replicates. It has been well established that genes have different biological variance, and thus we should not expect a constant ϕg for all genes. In experiments with a small number of replicates, an empirical Bayes method that combines the information from the observed sample and shrinks toward a common prior of ϕg helps stabilize the estimate of ϕg. However, the extent of shrinkage should not be uniform as the amount of information about ϕg varies between genes. The variation of counts from genes with low expression is dominated by the Poisson counting error, and provides less information of ϕg (supplementary material available at Biostatistics online, Figure S10) ; thus the estimates of ϕg for these genes should be shrunken more heavily . DSS does exactly what we desire, shrinking ϕg less for high-expression genes and more for low-expression genes (Figure1(c)).
It has been reported that the biological variation, thus the dispersion parameter, may depend on the expression level. DESeq and EdgeR allow trended estimation of the dispersion depending on the mean level. To account for this dependence, we also provide an option in DSS by letting the hyper-parameter m0 be a smooth function of expression. The details of the trended estimation is provided in supplementary material available at Biostatistics online.
Some datasets are generated to investigate technical reproducibility and do not capture the biological variation in a population. Even in these cases with technical replicates only, such as the MAQC data, we find that analysis assuming a not-too-small dispersion provides improvement in DE detection (supplementary material available at Biostatistics online, Figure S12). When biological replicates are from established cell lines or inbred animal models, the variance among replicates may be lower than the variance in a random human population. However, the result on MAQC data with technical replicates suggests that even when there is no strong evidence for over-dispersion in the data, it is beneficial to analyze the data under a positive dispersion model.
We find that most of the improvement obtained in DSS is due to the different dispersion estimate, as passing the DSS estimates to edgeR/DESeq yields very similar results as in DSS (supplementary material available at Biostatistics online, Figure S9). Both the edgeR and the DESeq methods have been expanded to now accommodate multiclass comparisons. Our test is currently limited to two-class comparison and it is our immediate plan to extend the dispersion estimators to multifactor designs. With an estimate of the dispersion, one can use generalized linear models as done in McCarthy and others (2012).
In all comparisons presented here, we use semiparametric simulation based on real RNA-seq datasets for lack of real data example with known truth. Although the NB model is the current predominant choice for RNAseq data, most models only approximate reality. Real data with a reasonable number of known DE, for example, using spike-in genes, will enable better comparison.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Funding
This research was supported by National Science Foundation (DBI-1054905).
Supplementary Material
Acknowledgments
The authors thank the anonymous reviewers for their insightful and constructive comments. Conflict of Interest: None declared.
References
- Anders S., Huber W. Differential expression analysis for sequence count data. Genome Biology. 2010;11:R106. doi: 10.1186/gb-2010-11-10-r106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blekhman R., Marioni J. C., Zumbo P., Stephens M., Gilad Y. Sex-specific and lineage-specific alternative splicing in primates. Genome Research. 2010;20:180–189. doi: 10.1101/gr.099226.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullard J. H., Purdom E., Hansen K. D, Dudoit S. Evaluation of statistical methods for normalization and differential expression in mRNA-Seq experiments. BMC Bioinformatics. 2010;11:94. doi: 10.1186/1471-2105-11-94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung V. G., Nayak R. R., Wang I. X., Elwyn S., Cousins S. M., Morley M., Spielman R. S. Polymorphic Cis- and Trans-regulation of human gene expression. PLoS Biology. 2010;8:e1000480. doi: 10.1371/journal.pbio.1000480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B. Large-scale simultaneous hypothesis testing. Journal of the American Statistical Association. 2004;99:96–104. [Google Scholar]
- Frazee A., Langmead B., Leek J. Recount: a multi-experiment resource of analysis-ready RNA-seq gene count datasets. BMC Bioinformatics. 2011;12:449. doi: 10.1186/1471-2105-12-449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibbs R. A., Belmont J. W., Hardenbol P., Willis T. D., Yu F., Yang H., Ch’ang L. Y., Huang W., Liu B., Shen Y. and others. The international hapmap project. Nature. 2003;426:789–796. doi: 10.1038/nature02168. [DOI] [PubMed] [Google Scholar]
- Hansen K. D., Irizarry R. A., Wu Z. Removing technical variability in RNA-seq data using conditional quantile normalization. Biostatistics. 2012;13:204–216. doi: 10.1093/biostatistics/kxr054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen K. D., Wu Z., Irizarry R. A., Leek J. T. Sequencing technology does not eliminate biological variability. Nature Biotechnology. 2011;29:572–573. doi: 10.1038/nbt.1910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardcastle T., Kelly K. Bayseq: empirical bayesian methods for identifying differential expression in sequence count data. BMC Bioinformatics. 2010;11:422. doi: 10.1186/1471-2105-11-422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marioni J. C., Mason C. E., Mane S. M., Stephens M., Gilad Y. RNA-seq: an assessment of technical reproducibility and comparison with gene expression arrays. Genome Research. 2008;18:1509–1517. doi: 10.1101/gr.079558.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCall M. N., Uppal K., Jaffee H. A., Zilliox M. J., Irizarry R. A. The gene expression barcode: leveraging public data repositories to begin cataloging the human and murine transcriptomes. Nucleic Acids Research. 2011;39(Suppl 1):D 1011. doi: 10.1093/nar/gkq1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy D. J., Chen Y., Smyth G. K. Differential expression analysis of multifactor RNA-seq experiments with respect to biological variation. Nucleic Acids Research. 2012 doi: 10.1093/nar/gks042. ( doi:10.1093/nar/gks042) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickrell J. K., Marioni J. C., Pai A. A., Degner J. F., Engelhardt B. E., Nkadori E., Veyrieras J.-B., Stephens M., Gilad Y., Pritchard J. K. Understanding mechanisms underlying human gene expression variation with RNA sequencing. Nature. 2010;464:768–772. doi: 10.1038/nature08872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard C. C., Hsu L., Delrow J., Nelson P. S. Project normal: defining normal variance in mouse gene expression. Proceedings of the National Academy of Sciences. 2001;98:13266. doi: 10.1073/pnas.221465998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risso D., Schwartz K., Sherlock G., Dudoit S. GC-content normalization for RNA-seq data. BMC Bioinformatics. 2012;12:480–496. doi: 10.1186/1471-2105-12-480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson M. D., McCarthy D. J., Smyth G. K. edgeR: a Bioconductor package for differential expression analysis of digital gene expression dataSMotn. Bioinformatics. 2010;26:139–140. doi: 10.1093/bioinformatics/btp616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson M. D., Smyth G. K. Moderated statistical tests for assessing differences in tag abundance. Bioinformatics. 2007;23:2881–2887. doi: 10.1093/bioinformatics/btm453. [DOI] [PubMed] [Google Scholar]
- Robinson M. D, Smyth G. K. Small-sample estimation of negative binomial dispersion, with applications to SAGE data. Biostatistics. 2008;9:321–332. doi: 10.1093/biostatistics/kxm030. [DOI] [PubMed] [Google Scholar]
- Shi L., Reid L. H., Jones W. D., Shippy R., Warrington J. A., Baker S. C., Collins P. J., De Longueville F., Kawasaki E. S., Lee K. Y. and others. The microarray quality control (maqc) project shows inter-and intraplatform reproducibility of gene expression measurements. Nature Biotechnology. 2006;24:1151–1161. doi: 10.1038/nbt1239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smyth G. K. Linear models and empirical bayes methods for assessing differential expression in microarray experiments. Statistical Applications in Genetics and Molecular Biology. 2004;3:3. doi: 10.2202/1544-6115.1027. [DOI] [PubMed] [Google Scholar]
- Tusher V. G., Tibshirani R., Chu G. Significance analysis of microarrays applied to the ionizing radiation response. Proceedings of the National Academy of Sciences. 2001;98:5116. doi: 10.1073/pnas.091062498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L., Feng Z., Wang X., Zhang X. Degseq: an r package for identifying differentially expressed genes from RNA-seq data. Bioinformatics. 2010;26:136–138. doi: 10.1093/bioinformatics/btp612. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.

