Күк сфераһы
| Күк сфераһы | |
 | |
 | |
| Һүрәтләнгән объект | наблюдаемая Вселенная[d] |
|---|---|
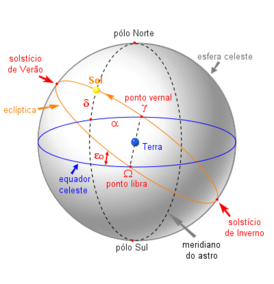 | |

Күк сфераһы (лат. orbis coelestis. ) - күк есемдәре проекцияланған ирекле радиуслы итеп күҙ алдына килтерелгән сфера: төрлө астрометрик мәсьәләләрҙе хәл итеү өсөн хеҙмәт итә. Күк сфераһының үҙәге итеп күҙәтеүсенең күҙҙәре ҡабул ителә; шул уҡ ваҡытта күҙәтеүсе Ер өҫтөндә лә, арауыҡтың башҡа нөктәләрендә лә була ала (мәҫәлән, ул Ер үҙәгенә индерелергә мөмкин). Ер өҫтөндәге күҙәтеүсе өсөн күк сфераһының әйләнеүе күктәге яҡтыртҡыстың тәүлеклек хәрәкәтен ҡабатлай.
Һәр бер күк яҡтыртҡысына күк сфераһының ярашлы нөктәһе тура килә, унда уны сфера үҙәген яҡтылыҡ үҙәге менән тоташтырған тура һыҙыҡ киҫеп үтә. Яҡтыртҡыстың күк сфераһындағы тороштарын һәм күренгән хәрәкәттәрен өйрәнгәндә теге йәки был сферик координаталар системаһы һайлана. Яҡтыртҡыстың күк сфераһындағы торошон иҫәпләүҙәр күк механикаһы һәм сферик тригонометрия ярҙамында башҡарыла һәм сферик астрономия фәнен тәшкил итә.
Тарихы
[үҙгәртергә | сығанаҡты үҙгәртеү]Күк сфераһы тураһында күҙаллау боронғо замандарҙа барлыҡҡа килә; уның нигеҙендә көмбәҙ рәүешендәге күк көмбәҙенең булыуы тураһында күренеш тәьҫораттары ята. Был тәьҫорат күктәге яҡтыртҡыстарҙың үтә алыҫ булыуы һөҙөмтәһендә кеше күҙе уларға тиклемге араларҙың төрлөсә алыҫлыҡта урынлашыуын билдәләй алмауына бәйле, һәм уларға күктәге яҡтыртҡыстар бер төрлө алыҫлыҡта булып күренә. Боронғо халыҡтарҙа был күренеш бөтә донъяны сикләүсе һәм үҙенең өҫтөндә күп һанлы йондоҙҙар йөрөткән реаль сфераның булыуы менән бәйле тип таныла. Шулай итеп, уларҙың күҙаллауы буйынса күк сфераһы Ғаләмдең иң мөһим элементы булып тора. Фәнни белем үҫеше менән күк сфераһына ҡарата бындай ҡараш юҡҡа сыға. Әммә боронғо заманда булдырылған күк сфераһы геометрияһы, үҫеш һәм камиллаштырыу стадияларын кисереп, хәҙерге заманда астрометрияла ла ҡулланылған күренешенә эйә була
Күк сфераһы элементтары
[үҙгәртергә | сығанаҡты үҙгәртеү]Текә һыҙыҡ һәм уның менән бәйле төшөнсәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]
Текә һыҙыҡ (йәки вертикаль һыҙыҡ) — күк сфераһы үҙәге аша үткән һәм күҙәтеү урынында ауыртмаҡтың (отвес) йүнәлеше менән тап килгән тура һыҙыҡ. Ауыртмаҡ һыҙығы күк сфераһы өҫтөндә ике нөктәлә киҫешә — күҙәтеүсе башы өҫтөндәге зенит һәм күҙәтеүсе аяҡтары аҫтындағы надирҙа.
Ысын (математик, йәки астрономик) офоҡ (горизонт) — күк сфераһының ҙур түңәрәге, уның яҫылығы ауыртмаҡ һыҙығына ҡарата перпендикуляр. Ысын офоҡ күк сфераһының өҫкө йөҙөн ике ярымсфераға бүлә: түбәһе зенитта булған күҙгә күренгән ярымсфера һәм түбәһе надирҙа булған күҙгә күренмәгән ярымсфера. Күҙәтеү нөктәһенең ер өҫтөнән бер аҙ юғарыраҡ урынлашыуы, шулай уҡ яҡтылыҡ нурҙарының атмосферала бөгөлөүе арҡаһында, ысын офоҡ күренгән офоҡ менән тап килмәй.
Бейеклек ҡулсаһы, йәки вертикал, яҡтыртҡыс — яҡтыртҡыс, зенит һәм надир аша үткән күк сфераһының ҙур ярымшары. Альмукантара́т (ғәрәп. «Тигеҙ бейеклектәр түңәрәге») — күк сфераһының бәләкәй түңәрәге, уның өҫтө математик горизонтҡа параллель рәүештә тора. Бейеклек һәм альмукантараттарҙың түңәрәктәре яҡтыртҡыстың горизонталь координаттарын биреүсе координат селтәрен барлыҡҡа килтерә.
Күк сфераһының тәүлек әйләнеүе һәм уның менән бәйле төшөнсәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]Донъя күсәре - донъя үҙәге аша үткән күҙалланған һыҙыҡ, уның тирәләй күк сфераһы әйләнә. Донъя күсәре күк сфераһы яҫылығында ике нөктәлә — донъяның төньяҡ полюсында һәм донъяның көньяҡ полюсында киҫешә. Күк сфераһына эстән ҡарағанда күк сфераһы төньяҡ полюс тирәләй сәғәт уҡтарына ҡаршы әйләнә.
Күк экваторы — күк сфераһының ҙур түңәрәге, уның яҫылығы донъя күсәренә ҡарата перпендикуляр һәм күк сфераһы үҙәге аша үтә. Күк экваторы күк сфераһын ике ярымшарға бүлә: төньяҡ һәм көньяҡ ярымшарҙар[1].
Яҡтыртҡыстың ауыш ҡулсаһы — күк сфераһының донъя полюстары һәм яҡтыртҡыс аша үткән ҙур ҡулсаһы.
Тәүлек параллеле — күк сфераһының бәләкәй түңәрәге, уның яҫылығы күк экваторына ҡарата параллель урынлашҡан, тимәк донъя күсәренә перпендикуляр. Яҡтыртҡыстарҙың күренгән тәүлек хәрәкәте тәүлек параллелдәре буйынса үтә. Төньяҡ күк ярымшары яҡтыртҡыстары күк сфераһы эсендә торған күҙәтеүсе өсөн донъяның төньяҡ полюсы тирәләй сәғәт теленә ҡаршы хәрәкәт итә,ә көньяҡ күк ярымшары яҡтыртҡысы донъяның көньяҡ полюсы тирәләй сәғәт теле буйынса хәрәкәт итә. Ауышлыҡ түңәрәктәре һәм тәүлек параллелдәре күк сфераһында координат селтәрен булдыра, ә ул үҙ сиратында яҡтыртҡыстың экваториаль координаттарын бирә.
"Текә һыҙыҡ" һәм "Күк сфераһының әйләнеше " төшөнсәләре киҫешкән урындарҙа барлыҡҡа килгән терминдар
[үҙгәртергә | сығанаҡты үҙгәртеү]Күк экваторы көнсығыш һәм көнбайыш нөктәләрендә математик горизонт менән киҫешә. Әйләнеүсе күк сфераһы нөктәләре офоҡтан күтәрелгән нөктә көнсығыш нөктәләре тип атала. Көнсығыш нөктәһе аша үткән бейеклектең ярым түңәрәге беренсе вертикаль тип атала.
Күк меридианы — күк сфераһының ҙур ҡулсаһы, уның яҫылығы текә һыҙыҡ һәм донъя күсәре аша үтә. Күк меридианы күк сфераһының өҫтөн ике ярымшарға бүлә: көнсығыш ярамшар һәм көнбайыш ярымшар.
Төш уртаһындағы һыҙыҡ — күк меридианы һәм математик горизонт яҫылыҡтары киҫешкән һыҙыҡ. Төш уртаһындағы һәм күк меридианы математик офоҡто ике нөктәлә киҫеп үтә: төньяҡ нөктәлә һәм көньяҡ нөктәлә. Донъяның төньяҡ полюсына яҡын урынлашҡаны төньяҡ нөктәһе тип атала.
Ҡояштың күк сфераһы буйлап йыллыҡ хәрәкәте һәм уның менән бәйле төшөнсәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]Эклиптика — күк сфераһының ҙур түңәрәге, уның буйынса Ҡояштың йыллыҡ хәрәкәте күҙәтелә. Эклиптика яҫылығы ε = 23°26' мөйөшөндә күк экваторы яҫылығы менән киҫешә.
Эклиптика күк экваторы менән киҫешкән ике нөктә көн менән төн тигеҙләнеше тип атала. Яҙғы көн менән төн тигеҙләнешендә Ҡояш үҙенең йыллыҡ хәрәкәтендә күк сфераһының көньяҡ ярымшарынан төньяҡ ярымшарына күсә; көҙгә көн менән төн тигеҙләнешендә төньяҡ ярымшарҙан көньяҡ ярымшарға күсә. Был ике нөктә аша үткән тура һыҙыҡ көн менән төн тигеҙләнеше һыҙығы[1] тип атала. Көн менән төн тигеҙләнеше нктәләренән 90° градус ситтәрәк торған һәм шуға күрә күк экваторынан максималь рәүештә алыҫлашҡан ике нөктә ҡояш торошо нөктәләре тип атала. Йәйге ҡояш торошо торошо нөктәһе төньяҡ ярымшарҙа, ҡышҡы ҡояш торошо нөктәһе көньяҡ ярымшарҙа була. Был дүрт нөктә зодиак символдары, Гиппарха[2] заманында улар урынлашҡан ярашлы йондоҙлоҡтар менән билдәләнә (көн менән төн тигеҙләнеше ғәмәлгә ашырыу һөҙөмтәһендә был нөктәләр урындарынан бер аҙ шыла, һәм хәҙер улар башҡа йондоҙлоҡтарҙа урынлашҡан): яҙғы көн менән төн тигеҙләнеше — Ҡуҙы (♈), көҙгө көн менән төн тигеҙләнеше — Үлсәү (♎), ҡышҡы ҡояш торошо — Кәзәмөгөҙ (♑), йәйге ҡояш торошо — Ҡыҫала (♋) билдәләре менән[3].
Эклиптика күсәре — эклиптика яҫылығына перпендикуляр булған күк сфераһы диаметры. Эклиптика күсәре ике нөктәлә күк сфераһы менән киҫешә — эклиптиканың төньяҡ ярымшарҙа ятҡан төньяҡ полюсында, эклиптиканың көньяҡ ярымшарҙа ятҡан көньяҡ полюсында. Эклиптиканың төньяҡ полюсының экваториаль координаттары R.A. = 18h00m, Dec = +66°33', һәм ул Аждаһа йондоҙлоғонда, ә көньяҡ полюс — R.A. = 6h00m, Dec = −66°33', һәм ул Алтын балыҡ йондоҙлоғонда.
Шулай уҡ ҡара
[үҙгәртергә | сығанаҡты үҙгәртеү]| Күк сфераһы Викимилектә |
Иҫкәрмәләр
[үҙгәртергә | сығанаҡты үҙгәртеү]- ↑ Весеннее равноденствие // Брокгауз һәм Ефрондың энциклопедик һүҙлеге: 86 томда (82 т. һәм 4 өҫтәмә том). — СПб., 1890—1907. (рус.)
- ↑ Левитан Е. Редкое астрономическое явление (рус.) // Наука и жизнь. — 1988. — № 9. — С. 116.
- ↑ Цесевич В.П. Эклиптика // Что и как наблюдать на небе. — 6-е изд. — М.: Наука, 1984. — С. 48—49. — 304 с.
Әҙәбиәт
[үҙгәртергә | сығанаҡты үҙгәртеү]- Веселовский И. Н. Астрономия орфиков // Вопросы истории естествознания и техники. — М., 1982. — № 2. — С. 120—124.
- Житомирский С. В. Древность небесных кругов // Земля и Вселенная. — 1998. — № 3. — С. 31—36.
- Матвиевская Г. П. Сферика и сферическая тригонометрия в древности и на средневековом востоке // Развитие методов астрономических исследований, Вып. 8. — М.—Л., 1979.
- Воронцов-Вельяминов Б.А., Е. К. Страут. Астрономия, Базовый уровень, 11 класс. — Дрофа, 2018. — 238 с.