চাকতি (গণিত)

একটি অ্যানুলাস

মামিকনের ভিজ্যুয়াল ক্যালকুলাস পদ্ধতির চিত্র দেখায় যে একই জ্যা দৈর্ঘ্যের দুটি চাকতির ক্ষেত্রগুলি ভিতরের এবং বাইরের ব্যাসার্ধ নির্বিশেষে একই।

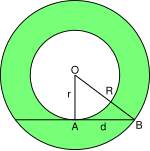
গাণিতিক ভাষায়, চাকতি হল দুটি সমকেন্দ্রিক বৃত্তের মধ্যবর্তী অঞ্চল। সাধারণ ভাষায়, এটি একটি রিং বা একটি বেসিনের মতো আকৃতি বিশিষ্ট জ্যামিতিক বস্তু।একে ইংরেজিতে "অ্যানুলাস" বলা হয়ে থাকে। " অ্যানুলাস'' শব্দটি ল্যাটিন শব্দ অ্যানুলাস বা অ্যানুলাস থেকে ধার করা হয়েছে যার অর্থ 'ছোট আংটি'।

টপোগণিতে চাকতি খোলা চোঙ (S¹ × (0,1)) এবং ছিদ্রযুক্ত সমতল উভয়েরই সম-অবিচ্ছিন্ন চিত্র।

ক্ষেত্রফল

ধরা যাক চাকতিটি দুটি বৃত্তের মাঝে অবস্থান করছে যাদের ব্যাসার্ধ যথাক্রমে R ও r, যেখানে R > r, তাহলে চাকতিটির ক্ষেত্রফল হবেঃ

$A=\pi R^{2}-\pi r^{2}=\pi \left(R^{2}-r^{2}\right).$

জ্যা সূত্রের ফলস্বরূপ, প্রতিটি একক উত্তল নিয়মিত বহুভুজের বৃত্ত এবং বৃত্ত দ্বারা আবদ্ধ এলাকা হল π /4

একটি চাকতির ক্ষেত্রফল তার মধ্যস্থ দীর্ঘতম রেখাংশের দৈর্ঘ্য দ্বারা নির্ধারিত হয়, যা বড় বৃত্তটির জ্যা এবং ক্ষুদ্রত্তর বৃত্তের স্পর্শক, সহগামী চিত্রে যা 2d । যেহেতু এই রেখাটি ছোট বৃত্তের স্পর্শক এবং সেই বৃত্ত ব্যাসার্ধ স্পর্শকটির উপর লম্ব তাইপিথাগোরাসের উপপাদ্য ব্যবহার করে দেখানো যেতে পারে d, r এবং R হল একটি সমকোণী ত্রিভুজের বাহু, সুতরাং চাকতিটির ক্ষেত্রফল হবেঃ

$A=\pi \left(R^{2}-r^{2}\right)=\pi d^{2}.$

ক্ষেত্রফলটি ক্যালকুলাসের মাধ্যমেও পাওয়া যেতে পারে। চাকতিটিকে অসীম সংখ্যক শূণ্যসন্নিকর্ষী dρ প্রস্থ এবং 2πρ dρ ক্ষেত্রফলযুক্ত চাকতিতে ভাগ করে ρ = r থেকে ρ = R পর্যন্ত সমাকলিত করলে আম্রা পাব:

$A=\int _{r}^{R}\!\!2\pi \rho \,d\rho =\pi \left(R^{2}-r^{2}\right).$

চাকতির কোনো অংশে θ কোণ উৎপন্ন হলে এবং যদি সেই কোণকে রেডিয়ানে মাপা হয় তবে চাকতির ক্ষেত্রফল হবেঃ

$A={\frac {\theta }{2}}\left(R^{2}-r^{2}\right).$

জটিল গঠন

জটিল বিশ্লেষণে জটিল সমতলে চাকতি বা জটিল বিশ্লেষণের ভাষায় ann(a; r, R) একটি উন্মুক্ত অঞ্চল যা কিনা

$r<|z-a|<R.$

দ্বারা চেনা যেতে পারে।