Natürliche Transformation

In der Kategorientheorie, einem Teilgebiet der Mathematik, stellt eine natürliche Transformation eine Möglichkeit dar, einen Funktor in einen anderen zu transformieren, und das unter Beibehaltung der inneren Struktur der beteiligten Kategorien, das heißt der Kompositionen von Morphismen. Tatsächlich kann diese Intuition so formalisiert werden, dass man zum Begriff der sogenannten Funktorkategorie gelangt. Natürliche Transformationen gehören nach Kategorien und Funktoren zu den fundamentalsten Begriffen der Kategorientheorie und kommen daher in der Mehrzahl ihrer Anwendungen vor.

Definition

Seien $F$ und $G$ Funktoren zwischen den Kategorien ${\mathcal {C}}$ und $D$. Eine natürliche Transformation $\eta$ von $F$ nach $G$ ist eine Familie von Morphismen $\eta =(\eta _{X})_{X\in {\mathcal {C}}}$, so dass Folgendes gilt:

1. Für jedes Objekt $X$ in ${\mathcal {C}}$ ist $\eta _{X}$ ein Morphismus $\eta _{X}:F(X)\rightarrow G(X)$ in ${\mathcal {D}}$. Der Morphismus $\eta _{X}$ heißt die Komponente von $\eta$ bei $X$.
2. Die Komponenten von $\eta$ erfüllen für jeden Morphismus $f:X\rightarrow Y$ in ${\mathcal {C}}$ die Gleichung

$\eta _{Y}\circ F(f)=G(f)\circ \eta _{X}$.

Diese Gleichung wird übersichtlich durch folgendes kommutatives Diagramm ausgedrückt:

Dies ist das kommutative Diagramm zur Definition der natürlichen Transformation zwischen zwei Funktoren.

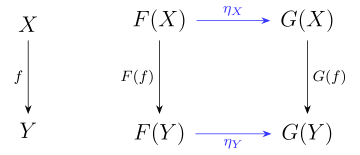
Sind beide Funktoren $F$ und $G$ kontravariant, so kehren sich die vertikalen Pfeile in obigem Diagramm um. Ist $\eta$ eine natürliche Transformation von $F$ nach $G$, so schreibt man $\eta :F\to G$ oder $\eta :F\implies G$. Das drückt man auch durch die Redeweise aus, dass die Familie von Morphismen $\eta _{X}:F(X)\to G(X)$ natürlich in $X$ sei.

Wenn alle Komponenten $\eta _{X}$ Isomorphismen in ${\mathcal {D}}$ sind, so nennt man $\eta$ einen natürlichen Isomorphismus oder eine natürliche Äquivalenz oder einen Isomorphismus der Funktoren. Zwei Funktoren $F$ und $G$ heißen natürlich isomorph oder einfach isomorph, wenn es einen natürlichen Isomorphismus von $F$ nach $G$ gibt.

Zu einer beliebigen Familie $\eta =(\eta _{X})_{X\in {\mathcal {C}}}$ von Morphismen $\eta _{X}:F(X)\to G(X)$ gibt es eine größte Unterkategorie von ${\mathcal {C}}$, so dass die Einschränkung darauf einen natürliche Transformation ist. Sie besteht aus allen Objekten von ${\mathcal {C}}$ und allen Morphismen in ${\mathcal {C}}$, die obige Bedingung erfüllen.

Beispiele

Gegengruppen

Jede Gruppe ist natürlich isomorph zu ihrer Gegengruppe. Aussagen dieser Art kommen in der modernen Mathematik sehr häufig vor. Wir wollen die genaue Bedeutung dieser Aussage und auch ihren Beweis wiedergeben.

Betrachte die Kategorie ${\textbf {Grp}}$ aller Gruppen mit den Gruppenhomomorphismen als Morphismen. Ist $(G,*)$ eine Gruppe, so definieren wir ihre Gegengruppe $(G^{\text{op}},{*}^{\text{op}})$ wie folgt: $G^{\text{op}}$ ist dieselbe Menge wie $G$ und die Gruppenoperation $*^{\text{op}}$ wird definiert durch $a*^{\text{op}}b=b*a$. In diesem Sinne sind alle Multiplikationen in $G^{\text{op}}$ „umgedreht“. Der Übergang zur Gegengruppe wird zu einem kovarianten Funktor von ${\textbf {Grp}}$ nach ${\textbf {Grp}}$, wenn wir $f^{\text{op}}:=f$ für jeden Homomorphismus $f:G\to H$ definieren. Beachte, dass $f^{\text{op}}$ tatsächlich ein Gruppenhomomorphismus $G^{\text{op}}\rightarrow H^{\text{op}}$ ist, denn

$f^{\text{op}}(a*^{\text{op}}b)=f(b*a)=f(b)*f(a)=f^{\text{op}}(a)*^{\text{op}}f^{\text{op}}(b).$

Der Inhalt obiger Aussage ist:

„Der identische Funktor ${\text{Id}}_{\textbf {Grp}}:{\textbf {Grp}}\to {\textbf {Grp}}$ ist natürlich isomorph zu ${\text{op}}:{\textbf {Grp}}\to {\textbf {Grp}}$.“

Zum Beweis müssen wir für jede Gruppe einen Homomorphismus $\eta _{G}:G\to G^{\text{op}}$ finden, so dass obiges Diagramm kommutiert. Dazu setze $\eta _{G}(a)=a^{-1}$. Die Formeln $(a*b)^{-1}=b^{-1}*a^{-1}=a^{-1}*^{\text{op}}b^{-1}$ und $(a^{-1})^{-1}=a$ zeigen, dass $\eta _{G}$ ein Gruppenhomomorphismus mit der Umkehrung $\eta _{G^{\text{op}}}$ ist. Zum Nachweis der Natürlichkeit gehen wir von einem Gruppenhomomorphismus $f:G\to H$ aus und zeigen $\eta _{H}\circ f=f^{\text{op}}\circ \eta _{G}$, das heißt $(f(a))^{-1}=f^{\text{op}}(a^{-1})$ für alle $a$ in $G$. Das gilt, weil $f^{\text{op}}=f$ und jeder Gruppenhomomorphismus die Eigenschaft $(f(a))^{-1}=f(a^{-1})$ hat.

Abelisierung

Zu einer Gruppe $G$ betrachten wir ihre Abelisierung $G^{\text{ab}}:=G/[G,G]$. Sei $\pi _{G}:G\to G^{\text{ab}}$ die Quotientenabbildung auf die Menge der Nebenklassen von [G,G] . Dieser Homomorphismus ist natürlich in $G$, wie wir nun zeigen werden. Sei $H$ eine Gruppe und $f:G\to H$ ein Homomorphismus. Dann ist $[G,G]$ im Kern von $\pi _{H}\circ f$ enthalten, denn jeder Homomorphismus in eine abelsche Gruppe bildet jeden Kommutator auf das neutrale Element ab. Dann faktorisiert $\pi _{H}\circ f$ über $G^{\text{ab}}$ als $f^{\text{ab}}\circ \pi _{G}=\pi _{H}\circ f$ mit einem eindeutigen Homomorphismus $f^{\text{ab}}:G^{\text{ab}}\to H^{\text{ab}}$. Das macht ${\text{ab}}:{\textbf {Grp}}\to {\textbf {Grp}}$ zu einem Funktor und $\pi =(\pi _{G})_{G\in {\textbf {Grp}}}$ zu einer natürlichen Transformation vom identischen Funktor zu ${\text{ab}}$, allerdings nicht zu einem natürlichen Isomorphismus.

Hurewicz-Homomorphismus

Die algebraische Topologie ist reich an Funktoren und natürlichen Transformationen. Als Beispiel betrachten wir den Hurewicz-Homomorphismus. Für jeden punktierten topologischen Raum $(X,x)$ und jede positive natürliche Zahl $n$ existiert ein Gruppenhomomorphismus

$h_{n}\colon \pi _{n}(X,x)\to H_{n}(X)$

von der $n$-ten Homotopiegruppe von $(X,x)$ in die $n$-te singuläre Homologiegruppe von $X$. Sowohl $\pi _{n}$ als auch $H_{n}$ sind Funktoren von der Kategorie Top^* der punktierten topologischen Räume in die Kategorie Grp der Gruppen und $h_{n}$ ist eine natürliche Transformation von $\pi _{n}$ nach $H_{n}$.

Determinante

Sind $R$ und $S$ kommutative Ringe und $f:R\to S$ ein Ringhomomorphismus, so definiert $f$ durch komponentenweise Anwendung von $f$ einen Gruppenhomomorphismus ${\text{GL}}_{n}(f)$ von ${\text{GL}}_{n}(R)$ nach ${\text{GL}}_{n}(S)$, wobei ${\text{GL}}_{n}(R)$ die Gruppe der invertierbaren Matrizen über $R$ mit $n$ Zeilen und $n$ Spalten sei. Ganz ähnlich ist die Einschränkung von $f$ ein Gruppenhomomorphismus $f^{*}:R^{*}\to S^{*}$, wobei $R^{*}$ die Einheitengruppe von $R$ sei. Tatsächlich sind hierdurch Funktoren ${\text{GL}}_{n}$ und $*$ von der Kategorie der kommutativen Ringe ${\textbf {CRing}}$ in die Kategorie der Gruppen ${\textbf {Grp}}$ gegeben. Die Einschränkung der Determinante ${\text{det}}_{R}$ auf ${\text{GL}}_{n}(R)$ ist ein Homomorphismus

${\mbox{det}}_{R}\colon {\mbox{GL}}_{n}(R)\to R^{*}$,

der natürlich in $R$ ist, denn da die Determinante für jeden Ring durch dieselbe Formel definiert ist, gilt $f\circ {\text{det}}_{R}={\text{det}}_{S}\circ {\text{GL}}_{n}(f)$. Dies macht die Determinate zu einer natürlichen Transformation von ${\text{GL}}_{n}$ nach $*$.

Bidual eines Vektorraums

Ist $K$ ein Körper, so ist für jeden Vektorraum $V$ über $K$ eine „natürliche“, injektive, lineare Abbildungen $V\to V^{**}$ des Vektorraums in seinen Bidualraum definiert. Diese Abbildungen sind in folgendem Sinne natürlich: Die Zuordnung zum Bidualraum ist ein Funktor, und die Abbildungen $V\to V^{**}$ sind die Komponenten einer natürlichen Transformation vom identischen Funktor zum Bidualraum-Funktor.

Endliche Analysis

Für jede abelsche Gruppe $G$ bildet die Menge ${\text{Hom}}_{\textbf {Set}}(\mathbb {Z} ,U(G))$ der Funktionen von den ganzen Zahlen in die unterliegende Menge von $G$ eine mit $V_{\mathbb {Z} }(G)$ bezeichnete abelsche Gruppe bezüglich der punktweisen Addition. Hierbei ist $U$ der übliche Vergissfunktor $U:{\textbf {Ab}}\to {\textbf {Set}}$. Ist $\varphi :G\to G'$ ein ${\textbf {Ab}}$-Morphismus, so ist die Abbildung $V_{\mathbb {Z} }(\varphi ):V_{\mathbb {Z} }(G)\to V_{\mathbb {Z} }(G')$, $f\mapsto \varphi \circ f$ selbst ein Homomorphismus abelscher Gruppen. Auf diese Weise erhalten wir einen Funktor $V_{\mathbb {Z} }:{\textbf {Ab}}\to {\textbf {Ab}}$. Der endliche Differenzoperator $\Delta _{G}$, der jede Funktion $f:\mathbb {Z} \to U(G)$ auf $\Delta _{G}(f):n\mapsto f(n+1)-f(n)$ abbildet, ist eine Abbildung von $V_{\mathbb {Z} }(G)$ in sich selbst. Die Familie $\Delta =(\Delta _{G})_{G\in {\textbf {Ab}}}$ dieser Abbildungen definiert eine natürliche Transformation $\Delta :V_{\mathbb {Z} }\to V_{\mathbb {Z} }$.

Tensor-Hom-Adjunktion

Betrachte die Kategorie ${\textbf {Ab}}$ der abelschen Gruppen und Gruppenhomomorphismen. Für je drei abelsche Gruppen gibt es einen Gruppenhomomorphismus

${\text{Hom}}(X\otimes Y,Z)\to {\text{Hom}}(X,{\text{Hom}}(Y,Z))$.

Diese Isomorphismen sind in dem Sinne natürlich, dass sie eine natürliche Transformation zwischen den Funktoren ${\text{Hom}}(-\otimes -,-)$ und ${\text{Hom}}(-,{\text{Hom}}(-,-))$ von ${\textbf {Ab}}^{\text{op}}\times {\textbf {Ab}}^{\text{op}}\times {\textbf {Ab}}\to {\textbf {Ab}}$ definieren. Hier steht „op“ für die duale Kategorie und nicht für den oben betrachteten (und auf ${\textbf {Ab}}$ trivialen) Funktor der Gegengruppen.

Dies ist formal die Adjunktion zwischen Tensorierung und Hom-Funktor, es handelt sich um den Archetyp eines Paares adjungierter Funktoren. Natürliche Transformationen treten häufig in Verbindung mit adjungierten Funktoren auf, tatsächlich sind adjungierte Funktoren mittels gewisser natürlicher Isomorphismen definiert. Zusätzlich ist jedes Paar adjungierter Funktoren mit zwei weiteren natürlichen Transformationen (die im Allgemeinen keine natürlichen Isomorphismen sind) verbunden, nämlich der Einheit und der Koeinheit.

Unnatürliche Isomorphismen

Der Begriff der natürlichen Transformation ist kategoriell und besagt, informell gesprochen, dass eine bestimmte Abbildung zwischen Funktoren in konsistenter Weise über die gesamte Kategorie hinweg erstellt werden kann. Einzelne Abbildungen, insbesondere Isomorphismen, zwischen einzelnen Objekten (also nicht auf der gesamten Kategorie gegeben) werden „natürlich“ bzw. „natürliche Isomorphismen“ genannt, wenn man ihre Definitionen derart auf die gesamte Kategorie ausdehnen kann, dass man eine natürliche Transformation zwischen Funktoren erhält. Die Formalisierung dieser Intuition war ein motivierendes Element in der Entwicklung der Kategorientheorie. Umgekehrt nennt man einen Isomorphismus zwischen einzelnen Objekten „unnatürlich“ oder „nicht natürlich“, wenn diese Abbildung nicht zu einer natürlichen Transformation auf der gesamten Kategorie ausdehnen kann. Ist ein Objekt $X$ gegeben und ein Funktor $G$ (der Einfachheit halber wählen wir den ersten der beteiligten Funktoren als identischen Funktor) und ist $\eta \colon X\to G(X)$ ein Isomorphismus, so kann die Unnatürlichkeit am einfachsten dadurch gezeigt werden, dass man einen Automorphismus $a\colon X\to X$ angibt, der nicht mit dem Isomorphismus kommutiert, das heißt $\eta \circ a\neq G(a)\circ \eta$. Will man die stärkere Aussage beweisen, dass $X$ und $G(X)$ nicht natürlich isomorph sind, ohne dabei einen bestimmten Isomorphismus zu betrachten, muss man für jeden Isomorphismus $\eta$ einen solchen nicht-kommutierenden Automorphismus $a$ finden. In manchen Fällen genügt dafür schon ein einziger Automorphismus für alle Kandidaten, in anderen Fällen muss man für jedes $\eta$ ein anderes passendes $a$ konstruieren. Die Morphismen der Kategorie spielen dabei eine Schlüsselrolle, im Extremfall einer Kategorie, in der die Identitäten die einzigen Morphismen sind, ist jede Familie $\eta =(\eta _{X})_{X}$ von Morphismen $\eta _{X}\colon F(X)\to G(X)$ für zwei gegebene Funktoren in eine andere Kategorie eine natürliche Transformation.

Das ist vergleichbar zu gewissen Konzepten aus der Gruppentheorie oder Modultheorie, bei denen Zerlegungen eines Objektes in direkte Summen „nicht natürlich“, oder eher „nicht eindeutig“ sind, da es Automorphismen gibt, die die direkte Summenzerlegung nicht erhalten. Ein Beispiel dafür ist der Hauptsatz über endlich erzeugte abelsche Gruppen.

Manche Autoren unterscheiden diese Begriffe auch in ihrer Schreibweise, sie verwenden $\cong$ für natürliche Isomorphismen, $\approx$ für unnatürliche Isomorphismen und $=$ für Gleichheit.

Beispiel: Fundamentalgruppe des Torus

Als Beispiel für die Unterscheidung zwischen funktoriellen Aussagen und solchen über individuelle Objekte betrachten wir Homotopiegruppen, speziell die Fundamentalgruppe des Torus $T$.

Die Homotopiegruppe eines Produktraums ist auf natürliche Weise gleich dem Produkt der Homotopiegruppen der Komponenten, $\pi _{n}((X,x_{0})\times (Y,y_{0}))\cong \pi _{n}((X,x_{0}))\times \pi _{n}((Y,y_{0}))$, wobei der Isomorphismus durch die Projektionen auf die beiden Faktoren gegeben ist. Das gilt im Wesentlichen deshalb, weil Abbildungen in einen Produktraum genau die Produkte der Abbildungen in die Komponenten sind. Das ist eine funktorielle Aussage.

Der Torus, der auf abstrakte Weise ein Produkt zweier Kreise ist, hat jedenfalls als Fundamentalgruppe $\mathbb {Z} ^{2}$, aber die Zerlegung $\pi _{1}(T,t_{0})\approx \mathbb {Z} \times \mathbb {Z}$ ist nicht natürlich:

$\pi _{1}(T,t_{0})\approx \pi _{1}(S^{1},x_{0})\times \pi _{1}(S^{1},y_{0})\cong \mathbb {Z} \times \mathbb {Z} =\mathbb {Z} ^{2}.$

Beachte die Verwendung von $\approx$, $\cong$ und $=$.

Dieser abstrakte Isomorphismus mit dem Produkt ist nicht natürlich, denn manche Automorphismen auf $T$ erhalten das Produkt nicht. Der Automorphismus (Homöomorphismus) auf dem Torus, den man sich als Quotientenraum $T=\mathbb {R} ^{2}/\mathbb {Z} ^{2}$ gegeben denke, der durch $\left({\begin{smallmatrix}1&1\\0&1\end{smallmatrix}}\right)$ gegeben ist (geometrisch ist das ein Dehn-Twist), erhält nicht die Produktstruktur, da die definierende Matrix nicht diagonal ist. Ist allerdings der Torus als Produkt gegeben, $(T,t_{0})=(S^{1},x_{0})\times (S^{1},y_{0})$, dann ergibt sich die Zerlegung der Gruppe wie oben angegeben durch die Projektionsabbildungen. Kategorientheoretisch ausgedrückt ist die hier relevante Kategorie die der Produkträume, die mit ihrer Produktstruktur gegeben sind, und den Abbildungen zwischen ihnen, die als Paare von Abbildungen zwischen den Komponenten gegeben sind.

Natürlichkeit ist ein kategorieller Begriff und erfordert eine präzise Angabe der vorliegenden Daten. Der Torus als topologischer Raum, der in der Kategorie der topologischen Räume und stetigen Abbildungen als ein Produkt geschrieben werden kann, ist etwas anderes als ein bereits als Produkt definierter Torus in der Kategorie der Produkte zweier topologischer Räume und den stetigen Abbildungen zwischen den Komponenten (denn die Kategorien sind andere).

Beispiel: Dualraum eines endlichdimensionalen Vektorraums

Jeder endlichdimensionale Vektorraum ist isomorph zu seinem Dualraum, aber es kann sehr viele verschiedene Isomorphismen zwischen diesen beiden Räumen geben. Im Allgemeinen gibt es keinen natürlichen Isomorphismus zwischen einem endlichdimensionalen Vektorraum und seinem Dualraum. Allerdings können verwandte Kategorien (mit zusätzlicher Struktur und Beschränkungen in den Morphismen) durchaus natürliche Isomorphismen dieser Art besitzen, wie unten ausgeführt wird.

Ein Dualraum eines endlichdimensionalen Vektorraums ist wieder ein endlichdimensionaler Vektorraum derselben Dimension, und daher sind die beiden isomorph, denn die Dimension ist die einzige Invariante endlichdimensionaler Vektorräume über einem gegebenen Körper. Ohne weitere Einschränkungen (wie zum Beispiel die Forderung, dass Abbildungen gewählte Basen erhalten) ist so ein Isomorphismus nicht eindeutig, von trivialen Ausnahmen abgesehen. Ein solcher Isomorphismus erfordert eine bestimmte Wahl, und das ist „nicht natürlich“. In der Kategorie der endlichdimensionalen Vektorräume und linearen Abbildungen kann man eine Familie von Isomorphismen zwischen Räumen und ihren Dualräumen bilden (etwa indem man Basen wählt und dann die zugehörigen Isomorphismen), aber eine solche Familie definiert niemals eine natürliche Transformation. Intuitiv liegt das an den zu treffenden Wahlen, mathematisch strikt liegt das daran, dass keine solche Wahl mit allen linearen Abbildungen kommutiert (wie in obiger Definition), siehe für eine detaillierte Diskussion.

Betrachtet man endlichdimensionale Vektorräume und darauf den identischen Funktor und den Dualraumfunktor, so kann man einen natürlichen Isomorphismus definieren, aber dazu muss man zusätzliche Struktur hinzufügen und die Morphismen von „beliebige lineare Abbildungen“ auf „diese Struktur erhaltende lineare Abbildungen“ einschränken. Genauer muss jeder endlichdimensionale Vektorraum eine Zusatzstruktur haben, die einen Isomorphismus $\eta _{V}\colon V\to V^{*}$ in den Dualraum festlegt. Dazu betrachtet man Vektorräume mit einer nicht-ausgearteten Bilinearform $b_{V}\colon V\times V\to K$. Dadurch erhält man eine Familie von Isomorphismen $\eta _{V}$ für jedes Objekt $V$ der Kategorie. Dann schränkt man die Morphismen auf diejenigen linearen Abbildungen $T\colon V\to U$ ein, die mit diesen Morphismen kommutieren, das heißt $T^{*}(\eta _{U}(T(v)))=\eta _{V}(v)$, oder mit anderen Worten, die die Bilinearform erhalten, das heißt $b_{U}(T(v),T(w))=b_{V}(v,w)$. Die so entstandene Kategorie, endlichdimensionale Vektorräume mit einer nicht-ausgearteten Bilinearform und lineare Abbildungen, die die Bilinearformen erhalten, hat nach Konstruktion einen natürlichen Isomorphismus von der Identität auf den Dualraumfunktor. Diese Art der Konstruktion – füge jedem Objekt eine Transformation als Zusatzstruktur hinzu und schränke die Morphismen auf solche ein, die diese Zusatzstruktur erhalten – hängt nicht von speziellen Eigenschaften der Vektorräume ab.

In dieser Kategorie (endlichdimensionale Vektorräume mit nicht-ausgearteter Bilinearform und lineare Abbildungen, die diese Bilinearformen erhalten), können die dualen Abbildungen mit Transpositionen identifiziert werden. Aus geometrisch motivierten Gründen interessiert man sich für spezielle Unterkategorien, bei denen man weitergehende Eigenschaften der nicht-ausgearteten Bilinearform fordert, etwa dass diese symmetrisch, symmetrisch und positiv definit, hermitesch oder schiefsymmetrisch ist. In all diesen Kategorien kann ein Vektorraum unter Benutzung der Bilinearform auf natürliche Weise mit seinem Dualraum identifiziert werden.

Operationen mit natürlichen Transformation

Sind $\eta :F\to G$ und $\epsilon :G\to H$ natürliche Transformationen der Funktoren $F,G,H:{\mathcal {C}}\to {\mathcal {D}}$, können wir sie zu einer natürlichen Transposition $\epsilon \eta :F\to H$ komponieren. Dies geschieht komponentenweise $(\epsilon \eta )_{X}=\epsilon _{X}\eta _{X}$.

Diese „vertikale Komposition“ natürlicher Transformationen ist assoziativ und hat identische Elemente (die identischen Transformationen von einem Funktor zu sich selbst). Dadurch kann man die Gesamtheit der Funktoren ${\mathcal {C}}\to {\mathcal {D}}$ mit den natürlichen Transformationen als Morphismen wieder zu einer Kategorie machen, zu einer sogenannten Funktorkategorie.

Natürliche Transformationen haben auch eine „horizontale Komposition“. Ist $\eta :F\to G$ eine natürliche Transformation zwischen Funktoren $F,G:{\mathcal {C}}\to {\mathcal {D}}$ und ist $\epsilon :J\to K$ eine natürliche Transformation zwischen Funktoren $J,K:{\mathcal {D}}\to {\mathcal {E}}$, dann erlaubt die Komposition der Funktoren eine natürliche Transformation $\epsilon *\eta :JF\to KG$ wobei $(\epsilon \ast \eta )_{X}=\epsilon _{G(X)}J(\eta _{X})$.

Diese Operation ist ebenfalls assoziativ und hat dieselben identischen Transformationen wie die vertikale Komposition.

Horizontal and vertical composition of natural transformations

Die beiden Operationen hängen über eine Beziehung zusammen, die vertikale und die horizontale Kompositionen sind vertauschbar. Haben wir vier natürliche Transformationen $\alpha ,\alpha ',\beta ,\beta '$ wie im nebenstehenden Bild, so gilt

$(\beta '\alpha ')*(\beta \alpha )=(\beta '*\beta )(\alpha '*\alpha ).$

Ist $\eta :F\to G$ eine natürliche Transformationen zwischen Funktoren $F,G:{\mathcal {C}}\to {\mathcal {D}}$ und ist $H:{\mathcal {D}}\to {\mathcal {E}}$ ein Funktor, so können wir durch

$(H\eta )_{X}=H(\eta _{X})$

die natürliche Transformation $H\eta :HF\to HG$ bilden. Ist auf der anderen Seite $K:{\mathcal {B}}\to {\mathcal {C}}$ ein weiterer Funktor, so wird durch

$(\eta K)_{X}=\eta _{K(X)}$

eine natürliche Transformation $\eta K:FK\to GK$ definiert. In diesen Fällen ist $H\eta =1_{H}*\eta$ bzw. $\eta K=\eta *1_{K}$.

Funktorkategorien

→ Hauptartikel: Funktorkategorie

Ist ${\mathcal {C}}$ irgendeine Kategorie und $I$ eine kleine Kategorie, so kann man die Funktorkategorie ${\mathcal {C}}^{I}$ bilden, die als Objekte alle Funktoren $I\rightarrow {\mathcal {C}}$ und als Morphismen alle natürlichen Transformationen zwischen diesen Funktoren hat. Dies bildet eine Kategorie, weil es zu jedem Funktor $F$ die identische natürliche Transformation $1_{F}:F\to F$ gibt und die Komposition (nämlich die oben beschriebene vertikale Komposition) zweier natürlicher Transformationen wieder eine natürliche Transformation ist.

Die Isomorphismen in ${\mathcal {C}}^{I}$ sind genau die natürlichen Isomorphismen. Das heißt eine natürliche Transformation $\eta :F\to G$ ist genau dann ein Isomorphismus, wenn es eine natürliche Transformation $\epsilon :G\to F$ gibt mit $\eta \epsilon =1_{G}$ und $\epsilon \eta =1_{F}$.

Die Funktorkategorie ${\mathcal {C}}^{I}$ ist besonders nützlich, falls $I$ ein gerichteter Graph zugrunde liegt. Ist zum Beispiel $I$ die Kategorie zum gerichteten Graphen „• → •“, so hat ${\mathcal {C}}^{I}$ als Objekte die Morphismen in ${\mathcal {C}}$ und ein Morphismus zwischen $\phi :U\to V$ und $\psi :X\to Y$ in ${\mathcal {C}}^{I}$ ist ein Paar von Morphismen $f:U\to X$ und $g:V\to Y$ in ${\mathcal {C}}$, so dass das „Quadrat kommutiert“, das heißt $\psi \circ f=g\circ \phi$.

Cat als 2-Kategorie

Allgemein hat man die 2-Kategorie ${\textbf {Cat}}$ mit

• allen kleinen Kategorien als Objekte,
• allen Funktoren zwischen den kleinen Kategorien als Morphismen,
• allen natürlichen Transformationen zwischen den Funktoren als 2-Morphismen.

Die horizontalen und vertikalen Kompositionen sind die oben beschriebenen Kompositionen zwischen den natürlichen Transformationen. Eine Funktorkategorie ${\mathcal {C}}^{I}$ ist dann einfach eine Hom-Menge in dieser Kategorie, wobei wir Kleinheitsprobleme beiseitelassen.

Weitere Beispiele

Jeder Limes und jeder Kolimes liefert ein Beispiel für eine einfache natürliche Transformation, denn ein Kegel ist eine natürliche Transformation zum Diagonalfunktor. Wenn man Limites und Kolimites mittels universeller Eigenschaften definiert, handelt es sich um universelle Morphismen in der Funktorkategorie.

Lemma von Yoneda

Ist ${\mathcal {C}}$ eine lokal kleine Kategorie (das heißt, die Morphismen zwischen je zwei Objekten bilden eine Menge), so ist die Zuordnung $Y\mapsto {\text{Hom}}_{\mathcal {C}}(X,Y)$ ein kovarianter Funktor $F_{X}:{\mathcal {C}}\to {\textbf {Set}}$. Ein solcher Funktor heißt darstellbar, allgemeiner ist ein darstellbarer Funktor ein Funktor, der natürlich isomorph zu einem Funktor dieser Art ist. Die natürlichen Transformationen von einem darstellbaren Funktor zu einem beliebigen Funktor sind vollständig bekannt und leicht zu beschreiben, dies ist genau der Inhalt des Lemmas von Yoneda.

Historische Bemerkungen

Saunders Mac Lane, einer der Begründer der Kategorientheorie, schreibt in: „Kategorien wurden definiert, um Funktoren definieren zu können, und Funktoren wurden definiert, um natürliche Transformationen definieren zu können.“ Genauso wie das Studium der Gruppen ohne das Studium der Gruppenhomomorphismen unvollständig ist, bleibt das Studium der Kategorien ohne die Untersuchung von Funktoren unvollständig. Nach Mac Lanes Kommentar ist auch das Studium der Funktoren ohne das Studium der natürlichen Transformationen unvollständig.

Ähnlich äußert sich Peter Freyd in:„Es ist zumindest historisch gesehen nicht zu abwegig, zu sagen, dass Kategorien das sind, was man definieren muss, um Funktoren zu definieren, und Funktoren das sind, was man definieren muss, um natürliche Transformationen zu definieren.“

Siehe auch

• Äquivalenz (Kategorientheorie)

Weblinks

• J. Adamek, H. Herrlich, G. Strecker, Abstract and Concrete Categories-The Joy of Cats
• Stanford Encyclopedia of Philosophy: "Category Theory"—von Jean-Pierre Marquis, mit umfangreichen Literaturangaben.