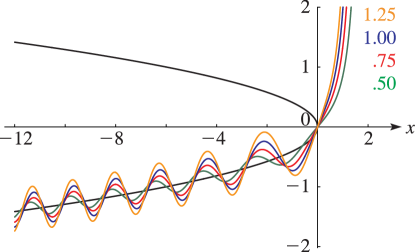§32.3 Graphics
Contents
- §32.3(i) First Painlevé Equation
- §32.3(ii) Second Painlevé Equation with
- §32.3(iii) Fourth Painlevé Equation with
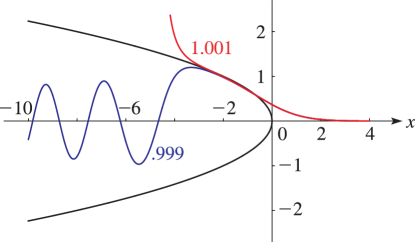
§32.3(i) First Painlevé Equation
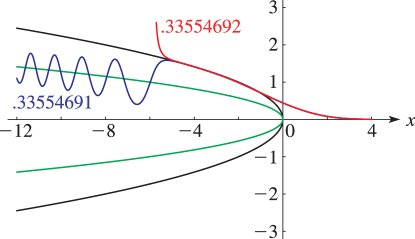
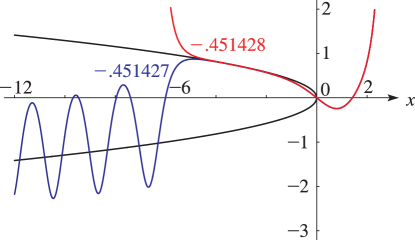
Plots of solutions of with and for various values of , and the parabola . For analytical explanation see §32.11(i).
§32.3(ii) Second Painlevé Equation with
§32.3(iii) Fourth Painlevé Equation with
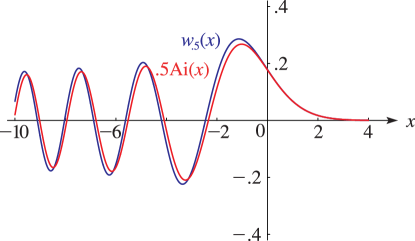
Here is the solution of
| 32.3.2 | |||
such that
| 32.3.3 | |||
| . | |||
The corresponding solution of is given by
| 32.3.4 | |||
with , , and
| 32.3.5 | |||
| ; | |||
compare (32.2.11) and §32.11(v). If we set in (32.3.2) and solve for , then
| 32.3.6 | |||