§5.9 Integral Representations
ⓘ
- Keywords:
- gamma function, integral representations
- Permalink:
- http://dlmf.nist.gov/5.9
- See also:
- Annotations for Ch.5
Contents
§5.9(i) Gamma Function
ⓘ
- Notes:
- For (5.9.1)–(5.9.2) see Olver (1997b, pp. 37–38). (5.9.3) follows from (5.2.1) by a change of variables. For (5.9.4)–(5.9.7), see Temme (1996b, pp. 43–45 and 77). (5.9.8) and (5.9.9) follow from (5.9.6) and (5.9.7). For (5.9.10) and (5.9.11) see Whittaker and Watson (1927, pp. 251 and 277).
- Permalink:
- http://dlmf.nist.gov/5.9.i
- Clarification (effective with 1.1.7):
- Equations (5.9.2_5), (5.9.10_1), (5.9.10_2), (5.9.11_1), (5.9.11_2) were added. Just below (5.9.11), () was changed to .
- See also:
- Annotations for §5.9 and Ch.5
| 5.9.1 | |||
|
ⓘ
| |||
, , and . (The fractional powers have their principal values.)
Hankel’s Loop Integral
ⓘ
- Keywords:
- Hankel’s loop integral, gamma function
- See also:
- Annotations for §5.9(i), §5.9 and Ch.5
| 5.9.2 | |||
|
ⓘ
| |||
where the contour begins at , circles the origin once in the positive direction, and returns to . has its principal value where crosses the positive real axis, and is continuous. See Figure 5.9.1.
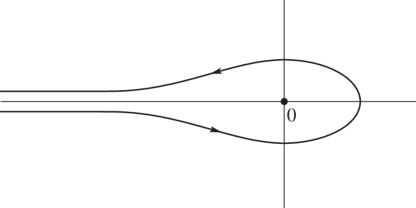
ⓘ
- Referenced by:
- §10.9(ii), §10.9(ii), §12.5(ii), §12.5(ii), §13.10(ii), §13.10(ii), §13.23(i), §13.23(i), §13.4(ii), §13.4(ii), (25.11.30), §25.11(vii), §25.11(vii), §25.5(iii), §25.5(iii), §5.9(i), Erratum (V1.2.1) for Figure 5.9.1, Erratum (V1.2.1) for Figure 5.9.1
- Permalink:
- http://dlmf.nist.gov/5.9.F1
- Encodings:
- pdf, png
- See also:
- Annotations for §5.9(i), §5.9(i), §5.9 and Ch.5
| 5.9.2_5 | |||
| , | |||
|
ⓘ
| |||
where .
| 5.9.3 | |||
| , , | |||
|
ⓘ
| |||
where the path is the real axis.
| 5.9.4 | |||
| . | |||
|
ⓘ
| |||
| 5.9.5 | |||
| . | |||
|
ⓘ
| |||
| 5.9.6 | ||||
| , | ||||
|
ⓘ
| ||||
| 5.9.7 | ||||
| . | ||||
|
ⓘ
| ||||
| 5.9.8 | |||
| , | |||
|
ⓘ
| |||
| 5.9.9 | |||
| . | |||
|
ⓘ
| |||
Binet’s Formula
ⓘ
- Keywords:
- Binet’s formula, gamma function, integral representations, logarithm
- See also:
- Annotations for §5.9(i), §5.9 and Ch.5
| 5.9.10 | |||
|
ⓘ
| |||
where and the inverse tangent has its principal value. Two alternative versions of Binet’s formula are
| 5.9.10_1 | |||
|
ⓘ
| |||
| 5.9.10_2 | |||
|
ⓘ
| |||
where .
| 5.9.11 | |||
|
ⓘ
| |||
where , , and is as in Chapter 25.
| 5.9.11_1 | |||
|
ⓘ
| |||
| 5.9.11_2 | |||
|
ⓘ
| |||
where , and the scaled gamma function is defined in (5.11.3). For additional representations see Whittaker and Watson (1927, §§12.31–12.32).
§5.9(ii) Psi Function, Euler’s Constant, and Derivatives
ⓘ
- Keywords:
- Euler’s constant, for derivatives, gamma function, integral representations, psi function
- Notes:
- See Olver (1997b, pp. 39–40), Temme (1996b, pp. 55–56), and Whittaker and Watson (1927, pp. 246–251). (5.9.15) and (5.9.17) are the differentiated forms of (5.9.10) and (5.9.11). (5.9.19) is the differentiated form of (5.2.1).
- Permalink:
- http://dlmf.nist.gov/5.9.ii
- Clarification (effective with 1.1.7):
- Just below (5.9.17) () was changed to .
- See also:
- Annotations for §5.9 and Ch.5
For ,
| 5.9.12 | |||
|
ⓘ
| |||
| 5.9.13 | |||
|
ⓘ
| |||
| 5.9.14 | |||
|
ⓘ
| |||
| 5.9.15 | |||
|
ⓘ
| |||
| 5.9.16 | |||
|
ⓘ
| |||
| 5.9.17 | |||
|
ⓘ
| |||
where and .
| 5.9.18 | |||
|
ⓘ
| |||
| 5.9.19 | |||
| , . | |||
|
ⓘ
| |||
