Número pi

| Números – Números irracionais ζ(3) – √2 – √3 – √5 – φ – α – e – π – δ | |
| Binario | 11,00100100001111110110… |
| Decimal | 3,14159265358979323846… |
| Hexadecimal | 3,243F6A8885A308D31319… |
| Fracción continua | Nótese que esta fracción continua non é periódica. |
Pi ou π é unha constante matemática cuxo valor é a razón aritmética de calquera circunferencia dun círculo co seu diámetro; este é o mesmo valor có da razón da área dun círculo co cadrado do seu raio. É aproximadamente igual a 3,14159 na notación decimal habitual. π é unha das constantes matemáticas e físicas máis importantes: moitas fórmulas das matemáticas, ciencias e enxeñaría están moi relacionadas con π[1].
π é un número irracional, o que significa que o seu valor non pode ser expresado exactamente como fracción m/n, onde m e n son enteiros. Por conseguinte, a súa representación decimal nunca acaba ou se repite. É tamén un número transcendente, o que quere dicir que non existen secuencias finitas de operacións alxébricas con números enteiros (multiplicacións, raíces, sumas etc.) que poidan ser igual ao seu valor; demostrar isto foi un logro recente na historia das matemáticas e un resultado significativo das matemáticas alemás do século XIX. Ao longo da historia matemática, teñen habido moitos esforzos por determinar π máis exactamente e entender a súa natureza; a fascinación co número mesmo pasou á cultura non-matemática.
A letra grega π, frecuentemente enunciada pi, foi adoptada para o número a partir da palabra grega para perímetro "περίμετρος", por vez primeira por William Jones en 1707, e popularizada por Leonhard Euler en 1737[2]. A constante tamén é ocasionalmente referida coma a "constante circular", a "constante de Arquímedes" (para non ser confundida co número de Arquimedes) ou "número de Ludolph" (na honra dun matemático alemán cuxos esforzos para calcular os máis dos seus díxitos fixérono coñecido).
Definicións
[editar | editar a fonte]- En xeometría plana, π pódese definir como a relación da circunferencia co seu diámetro.
- Tamén se define π analiticamente usando funcións trigonométricas, como exemplos:
- como o menor positivo x para o cal sen(x) = 0,
- como o duplo do menor positivo x para o cal cos(x) = 0.
A probabilidade e o número π
[editar | editar a fonte]
Unha lixeira reflexión pode facernos pensar que nada hai máis afastado do número π que o concepto de probabilidade, cando a realidade é ben distinta. O matemático e lóxico inglés Augustus De Morgan foi interrogado en certa ocasión por un vendedor de seguros sobre a probabilidade de que un grupo de persoas seguise con vida despois dun certo tempo. Na solución ao problema aparecía o número π, cousa que sorprendeu ao vendedor quen pensou que De Morgan se trabucara. A solución era a correcta e ten que ver coa distribución normal, unha variable aleatoria continua cuxa función de densidade é:
onde μ é a media e σ a desviación típica da distribución.
A distribución normal aparece ligada a multitude de situacións reais, entre elas á esperanza de vida do problema do vendedor de seguros. A gráfica desta distribución coñécese como campá de Gauss pola súa forma característica de campá e polo matemático alemán Gauss, quen en 1809 publicou un monográfico no que introducía algúns conceptos estatísticos, entre eles o de distribución normal; porén algúns autores atribúenlle o descubrimento en 1733 ao matemático francés De Moivre, estudando os coeficientes do binomio (a + b)n. É por este nome que Alexander Pope dicía que cada vez que alguén morre, as campás (de Gauss) soan por π.
Outros exemplos do campo das probabilidades onde aparece π son:
- A probabilidade de que dous enteiros positivos escollidos ó chou sexan primos entre si é
- Elixido ó chou un triángulo cuxo lado maior mide a unidade, a probabilidade de que sexa obtusángulo é
- O problema da agulla de Buffon: chamado así por ser proposto, e resolto, polo conde de Buffon, científico francés do século XVIII. Lanzada unha agulla, sen que se clave, sobre unha superficie na que se trazaron liñas paralelas equidistantes, trátase de calcular a probabilidade de que a agulla corte a unha liña. Se é a lonxitude da agulla, e a distancia entre as liñas, dita probabilidade é:
- cando
- cando
- cando
- O problema da agulla de Buffon-Laplace: foi proposto por Laplace en 1812. É unha variante do problema de Buffon considerando a superficie cuadriculada onde os lados da cuadrícula e non teñen por que medir o mesmo, e a lonxitude da agulla é menor que ambos lados.
- Se , a probabilidade de que a agulla corte a algún lado da cuadrícula é:
- Se , téñense as seguintes probabilidades:
- Probabilidade de que a agulla non corte a ningunha liña:
- Probabilidade de que a agulla corte a unha liña:
- Probabilidade de que a agulla corte ás dúas liñas:
- A suma das tres probabilidades anteriores é obviamente 1 xa que abarcan todas as posibilidades e corresponden a sucesos incompatíbeis.
Fórmulas que conteñen π
[editar | editar a fonte]Xeometría
[editar | editar a fonte]| Forma xeométrica | Fórmula |
|---|---|
| Circunferencia do círculo de raio r e diámetro d | |
| Área do círculo de raio r | |
| Área da elipse con semi-eixos a e mais b | |
| Volume da esfera de raio r | |
| Superficie da esfera de raio r | |
| Volume do cilindro de altura h e raio r | |
| Superficie do cilindro de altura h e raio r | |
| Volume do cono de altura h e raio r | |
| Superficie do cono de altura h e raio r |
Ademais, o ángulo 180° en graos equivale a π radiáns (unha volta enteira, 360 graos, son equivalentes a 2π radiáns).
Análise
[editar | editar a fonte]Moitas fórmulas de análise matemática conteñen π, incluíndo series infinitas, integrais, e as chamadas funcións especiais.
- fórmula de Leibniz:
- Esta serie infinita, citada a miúdo, escríbese como se indica arriba, pero exprésase máis tecnicamente como:
- produto de Wallis (ver este artigo para a proba):
- Unha fórmula de cálculo integral :
- problema de Basel, resolta por Euler (ver tamén función zeta de Riemann ):
- e xeralmente, é un múltiplo de para o enteiro positivo n
- función Gamma avaliada en 1/2:
- identidade de Euler (chamada por Richard Feynman "a fórmula máis salientada en matemáticas"):
- Area dun cuarto do círculo unidade:
Historia
[editar | editar a fonte]Antigüidade
[editar | editar a fonte]As aproximacións máis coñecidas a π datan de antes da nosa era e tiñan unha precisión de dúas cifras decimais; esta precisión mellorouse, sobre todo nas matemáticas chinesas en particular a mediados do primeiro milenio, ata unha precisión de sete cifras decimais. A partir de entón, non se produciron máis avances ata finais da Idade Media.
As primeiras aproximacións escritas de π atópanse en Babilonia e Exipto, ambas dentro do un por cento do valor verdadeiro. En Babilonia, unha tableta de arxila datada entre 1900 e 1600 a.C. ten un enunciado xeométrico que, implicitamente, trata a π como 25/8 = 3.125.[3] En Exipto, o papiro de Rhind, datado ao redor de 1650 AC pero copiado dun documento datado en 1850 AC, ten unha fórmula para a área dun círculo que trata a π como (16/9)2 ≈ 3.16.[4][3] Aínda que algúns piramidólogos como Flinders Petrie han teorizado que a Gran Pirámide de Gizeh foi construída con proporcións relacionadas con π, esta teoría non é amplamente aceptada polos estudosos.[5] Nos textos Shulba Sutras das matemáticas indias, que datan dunha tradición oral do primeiro ou segundo milenio a.C., danse aproximacións que foron interpretadas de diversas maneiras como aproximadamente 3.08831, 3.08833, 3.004, 3, ou 3.125.[6]
Era de aproximación de polígonos
[editar | editar a fonte]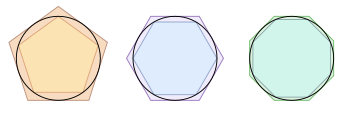

O primeiro algoritmo rexistrado para calcular rigorosamente o valor de π foi un enfoque xeométrico mediante polígonos, ideado ao redor do 250 a.C. polo matemático grego Arquímedes.[7] Este algoritmo poligonal dominou durante máis de 1.000 anos, e como resultado π coñécese ás veces como a constante de Arquímedes.[8] Arquímedes calculou os límites superior e inferior de π debuxando un hexágono regular dentro e fóra dun círculo, e duplicando sucesivamente o número de lados ata chegar a un polígono regular de 96 lados. Ao calcular os perímetros destes polígonos, demostrou que 223/71 < π < 22/7 (é dicir 3.1408 < π < 3.1429).[9] O límite superior de Arquímedes de 22/7 puido levar a unha crenza popular estendida de que π é igual a 22/7 .[10] Ao redor do 150 d. C., o científico grego-romano Tolomeo, no seu Almaxesto, deu un valor para π de 3,1416, que puido ter obtido de Arquímedes ou de Apolonio de Perge.[11][12] Os matemáticos que usaban algoritmos poligonais alcanzaron os 39 díxitos de π en 1630, un récord que só se bateu en 1699 cando se usaron series infinitas para acadar os 71 díxitos.[13]
Na China antiga, os valores de π eran 3,1547 (ao redor do ano 1 d. C.), √10 (aproximadamente 3.1623 no 100 d.C.), e 142/45 ( aproximadamente 3,1556 no século III).[14] Ao redor do 265 d. C., o matemático do reino Wei Li Hui creou un algoritmo iterativo baseado en polígonos e utilizouno cun polígono de 3.072 lados para obter un valor. de π de 3.1416.[15][16] Liu máis tarde inventou un método máis rápido para calcular π e obtivo un valor de 3,14 cun polígono de 96 lados, aproveitando que as diferenzas na área dos sucesivos polígonos forman unha serie xeométrica cun factor de 4.[15] O matemático chinés Zu Chongzhi, ao redor do ano 480 d. C., calculou que 3.1415926 < π < 3.1415927 e suxeriu as aproximacións π ≈ 355/113 = 3.14159292035... e π ≈ 22/7 = 3.142857142857..., que chamou Milü (''proporción proxima") e Yuelü ("proporción aproximada"), respectivamente, utilizando o algoritmo de Li Hui aplicado a un polígono de 12.288 lados. Cun valor correcto para os seus sete primeiros díxitos decimais, este valor seguiu sendo a aproximación máis exacta de π dispoñible durante os seguintes 800 anos.[17]
O astrónomo indio Âryabhata utilizou un valor de 3,1416 na súa Āryabhaṭīya (499 d. C.)..[18] Fibonacci en c. 1220 calculou 3,1418 mediante un método poligonal, independente de Arquímedes.[19] O autor italiano Dante ao parecer empregou o valor 3+√2/10 ≈ 3.14142.[19]
O astrónomo persa Jamshīd al-Kāshī produciu 9 díxitos sexaxesimais, aproximadamente o equivalente a 16 díxitos decimais, en 1424 utilizando un polígono con 3×228 lados,[20][21] que foi o récord mundial durante uns 180 anos.[22] O matemático francés François Viète logrou en 1579 9 díxitos cun polígono de 3×217 lados.[22] O matemático flamengo Adriaan van Roomen chegou os 15 decimais en 1593.[22] En 1596, o matemático holandés Ludolph van Ceulen alcanzou os 20 díxitos, un rexistro que máis tarde aumentou a 35 díxitos (como resultado, π foi chamado "número ludolphiano" en Alemaña ata principios do século XX).[23] O científico holandés Willebrord Snel alcanzou os 34 díxitos en 1621,[24] e o astrónomo austríaco Christoph Grienberger chegou a 38 díxitos en 1630 usando 1040 lados.[25] Christiaan Huygens foi quen de chegar a 10 cifras decimais en 1654 usando un método equivalente e lixeiramente diferente á extrapolación de Richardson.[26][27]
Series infinitas
[editar | editar a fonte]
O cálculo de π foi revolucionado polo desenvolvemento das técnicas de series infinitas nos séculos XVI e XVII. Unha serie infinita é a suma dos termos dunha sucesión infinita. As series infinitas permitían aos matemáticos calcular π con moita maior precisión que Arquímedes e outros que utilizaban técnicas xeométricas.[28] Aínda que as series infinitas foron explotadas para π sobre todo por matemáticos europeos como James Gregory e Gottfried Wilhelm Leibniz, o enfoque tamén apareceu na Escola de Kerala nalgún momento dos séculos XIV ou XV.[29][30] Ao redor de 1500 d. C., unha descrición escrita dunha serie infinita que podería usarse para calcular π foi presentada en verso sánscrito no tratado astronómico Tantrasamgraha escrito polo matemático e astronomo Nilakantha Somayaji.[29] As series preséntanse sen probas, pero as probas preséntanse nun traballo posterior, Yuktibhāṣā, de arredor de 1530 d.C. Descríbense varias series infinitas, incluíndo series para seno (que Nilakantha atribúe a Madhava de Sangamagrama), coseno e arcotanxente que agora se denominan ás veces series de Madhava. Ás veces a serie para arcotanxente chámase series de Gregory ou series Gregory–Leibniz.[29] Madhava utilizou series infinitas para estimar π a 11 díxitos ao redor de 1400, pero ese valor foi mellorado ao redor de 1430 polo matemático persa Jamshīd al-Kāshī, utilizando un algoritmo poligonal.[31]
En 1593, François Viète publicou o que agora se coñece como fórmula de Viète, un produto infinito (en lugar dunha suma infinita, que se utiliza máis tipicamente nos cálculos de π): [32][33][34]
En 1655, John Wallis publicou tamén un produto infinito, o que agora se coñece como produto de Wallis:[32]

Na década de 1660, o científico inglés Isaac Newton e o matemático alemán Gottfried Wilhelm Leibniz descubriron o cálculo, que conduciu ao desenvolvemento de moitas series infinitas para achegarse a π. O propio Newton utilizou unha serie arcoseno para calcular unha aproximación de 15 díxitos de π en 1665 ou 1666, escribindo "Avergóñame dicirche ata cantas cifras levei estes cálculos, non tendo outro asunto nese momento."[35]
En 1671, James Gregory , e independentemente Leibniz en 1673, descubriron a expansión da serie de Taylor para a función de arco:[29][36][37]
Esta serie, ás veces chamada serie de Gregory-Leibniz, é igual a π/4 cando se calcula con z = 1.[37] Pero para z = 1 converxe de forma pouco práctica (é dicir, aproxímase á resposta moi gradualmente), necesitando unhas dez veces máis termos para calcular cada díxito adicional.
En 1699, o matemático inglés Abraham Sharp utilizou a serie de Gregory-Leibniz para para calcular 71 díxitos de π, batendo o récord anterior de 39 díxitos, que se estableceu cun algoritmo poligonal.[38]
En 1706, John Machin utilizou a serie de Gregory-Leibniz para producir un algoritmo que converxía moito máis rápido:[39][40][41]
Machin alcanzou os 100 díxitos de π con esta fórmula.[42] Outros matemáticos crearon variantes, agora coñecidas como fórmulas de Machin, que se utilizaron para establecer varios récords sucesivos de cálculo de díxitos de π.[43][42]
Isaac Newton acelerou a converxencia da serie Gregory-Leibniz en 1684 (nun traballo inédito; outros descubriron de forma independente o mesmo resultado):[44]
Leonhard Euler popularizou esta serie no seu libro de texto de cálculo diferencial de 1755, e máis tarde utilizouna con fórmulas similares ás de Machin, incluíndo co que calculou 20 díxitos de π nunha hora.[45]
As fórmulas maquinais seguiron sendo o método máis coñecido para calcular π ata ben entrada a era dos computadores, e utilizáronse para establecer récords durante 250 anos, culminando cunha aproximación de 620 díxitos en 1946 por Daniel Ferguson - a mellor aproximación lograda sen a axuda dun dispositivo de cálculo.[46]
En 1844, Zacharias Dase estableceu un récord, que empregou unha fórmula similar a Machin para calcular 200 decimais de π coa súa cabeza a instancias do matemático alemán Carl Friedrich Gauss.[47]
En 1853, o matemático británico William Shanks calculou π ata os 607 díxitos, pero cometeu un erro no díxito 528, o que fixo que todos os díxitos posteriores fosen incorrectos. Aínda que en 1873 calculou 100 díxitos adicionais, co que o total ascendeu a 707, o seu erro anterior fixo que todos os novos díxitos tamén fosen incorrectos.[48]
Taxa de converxencia
[editar | editar a fonte]Algunhas series infinitas para π converxen máis rápido que outras. Dada a elección de dúas series infinitas para π, os matemáticos xeralmente usarán a que converxa máis rapidamente porque unha converxencia máis rápida reduce a cantidade de computación necesaria para calcular π con calquera precisión dada.[49] Unha serie infinita simple para π é a Serie de Gregory-Leibniz:[50]
A medida que se engaden termos individuais desta serie infinita á suma, o total achégase gradualmente a π, e - cun número suficiente de termos - pode achegarse tanto a π como se desexe. A converxencia é bastante lenta, aínda que - despois de 500.000 termos, só produce cinco díxitos decimais correctos de π.[51]
Unha serie infinita para π (publicada por Nilakantha no século XV) que converxe máis rapidamente que a serie de Gregory-Leibniz:[52][53]
Na táboa seguinte compáranse os índices de converxencia destas dúas series:
| Serie infinita para π | Despois do 1º termo | Despois do 2º termo | Despois do 3er termo | Despois do 4º termo | Despois do 5º termo | Converxe a: |
|---|---|---|---|---|---|---|
| 4.0000 | 2.6666 ... | 3.4666 ... | 2.8952 ... | 3.3396 ... | π = 3.1415 ... | |
| 3.0000 | 3.1666 ... | 3.1333 ... | 3.1452 ... | 3.1396 ... |
Despois de cinco termos, a suma da serie de Gregory-Leibniz está a 0,2 do valor correcto de π, mentres que a suma da serie de Nilakantha está a 0,002 do valor correcto. A serie de Nilakantha converxe máis rápido e é máis útil para calcular os díxitos de π. As series que converxen aínda máis rápido inclúen as series de Machin e de Chudnovsky, este último produce 14 díxitos decimais correctos por termo.[49]
Irracionalidade e transcendencia
[editar | editar a fonte]Non todos os avances matemáticos relacionados con π tiñan como obxectivo aumentar a precisión das aproximacións. Cando Euler resolveu o problema de Basilea en 1735, achando o valor exacto da suma dos cadrados recíprocos, estableceu unha conexión entre π e os números primos que máis tarde contribuíu ao desenvolvemento e estudo da función zeta de Riemann:[54]
O científico suízo Johann Heinrich Lambert demostrou en 1768 que π é un número irracional, o que significa que non é igual ao cociente de dous números enteiros calquera.[55] A proba de Lambert explotou unha representación de fracción continua da función tanxente.[56] O matemático francés Adrien-Marie Legendre demostrou en 1794 que π2 tamén é irracional. En 1882, o matemático alemán Ferdinand von Lindemann demostrou que π é un número transcendental,[57] confirmando unha conxectura feita tanto por Legendre como por Euler.[58][59] Hardy e Wright afirman que "as probas foron posteriormente modificadas e simplificadas por Hilbert, Hurwitz e outros escritores".[60]
Adopción do símbolo π
[editar | editar a fonte]Nos primeiros usos, a letra grega π utilizábase para denotar o semiperímetro (semiperipheria en latín) dun círculo[61] e combinábase en proporcións con δ (para diámetro ou semidiámetro) ou ρ (para raio) para formar constantes de círculo.[62][63][64][65] (Antes diso, os matemáticos ás veces utilizaban letras como c ou p no seu lugar.[66]) O primeiro uso rexistrado é o de Oughtred "", para expresar a relación entre periferia e diámetro nas edicións de 1647 e posteriores de Clavis Mathematicae.[67][66] Barrow igualmente utilizada "" para representar a constante 3.14...,[68] mentres que Gregory utilizaba no seu lugar "" para representar 6.28... .[69][64]
O uso máis antigo coñecido da letra grega π para representar a relación entre a circunferencia dun círculo e o seu diámetro foi realizado polo matemático galés William Jones na súa obra de 1706 Synopsis Palmariorum Matheseos; ou, A new Introduction to the Mathematics.[39][70] A letra grega aparece na p. 243 na frase " Periferia π)", calculada para un círculo de raio un. Con todo, Jones escribe que as súas ecuacións para π proveñen da "pluma lista do verdadeiramente enxeñoso Sr. John Machin", o que leva a especular que Machin puido empregar a letra grega antes que Jones.[66] A notación de Jones non foi adoptada inmediatamente por outros matemáticos, e a notación de fraccións seguía utilizándose en 1767.[62][71]
Euler empezou a utilizar a forma dunha soa letra a partir do seu Ensaio explicativo das propiedades do aire de 1727, aínda que utilizou π = 6,28..., o cociente entre a periferia e o raio, neste e nalgúns escritos posteriores.[72][73] Euler utilizou por primeira vez π = 3.14... na súa obra de 1736 Mechanica,[74] e continuou na súa moi lida obra de 1748 Introductio in analysin infinitorum (escribiu: «co fin da menor brevidade escribiremos este número como π; así π é igual á metade da circunferencia dun círculo de raio 1").[75] Como Euler mantiña unha gran correspondencia con outros matemáticos de Europa, o uso da letra grega estendeuse rapidamente, e a práctica adoptouse universalmente a partir de entón no mundo occidental,[66] aínda que a definición seguía variando entre 3,14... e 6,28... até 1761.[76]
Busca moderna de máis díxitos
[editar | editar a fonte]Era da informática e algoritmos iterativos
[editar | editar a fonte]O algoritmo iterativo de Gauss–Legendre:
Inicializar Iterar Entón unha estimación para π vén dada por |
O desenvolvemento dos computadores a mediados do século XX revolucionou de novo a procura de díxitos de π. Os matemáticos John Wrench e Levi Smith alcanzaron os 1.120 díxitos en 1949 utilizando unha calculadora de escritorio.[77] Utilizando unha serie infinita de tanxente inversa (arctan), un equipo dirixido por George Reitwiesner e John von Neumann conseguiu ese mesmo ano 2.037 díxitos cun cálculo que requiriu 70 horas de computador no ENIAC.[78][79] A marca, sempre baseado nunha serie arctan, bateuse repetidamente (3089 díxitos en 1955,[80] 7.480 díxitos en 1957; 10.000 díxitos en 1958; 100.000 díxitos en 1961) hasta alcanzar el millón de díxitos en 1973.[78]
Dous desenvolvementos adicionais ao redor de 1980 aceleraron de novo a capacidade de calcular π. En primeiro lugar, o descubrimento de novos algoritmos iterativos para calcular π, que eran moito máis rápidos que as series infinitas; e en segundo lugar, a invención de algoritmos de multiplicación rápida que podían multiplicar grandes números moi rapidamente.[81] Estes algoritmos son especialmente importantes nos cálculos π modernos porque a maior parte do tempo do computador dedícase á multiplicación.[82] Entre eles inclúense o algoritmo de Karatsuba, a multiplicación de Toom-Cook e os métodos baseados na transformada de Fourier.[83]
Notas
[editar | editar a fonte]- ↑ Howard Whitley Eves (1969). Holt, Rinehart & Winston, ed. An Introduction to the History of Mathematics.
- ↑ Comanor, Milton; Ralph P. Boas (1976). "Pi". En William D. Halsey. Collier's Encyclopedia 19. New York: Macmillan Educational Corporation. pp. 21–22.
- ↑ 3,0 3,1 Arndt & Haenel 2006, p. 167.
- ↑ Mollin, R. A. (1999). "Continued fraction gems". Nieuw Archief voor Wiskunde 17 (3). pp. 383–405. MR 1743850.
- ↑ Herz-Fischler, Roger (2000). The Shape of the Great Pyramid. Wilfrid Laurier University Press. pp. 67–77, 165–166. ISBN 978-0-88920-324-2. Arquivado dende o orixinal o 29 de novembro de 2016. Consultado o 22 de febreiro do 2023.
- ↑ Plofker, Kim (2009). Mathematics in India. Princeton University Press. p. 27. ISBN 978-0691120676.
- ↑ Arndt & Haenel 2006, p. 170.
- ↑ Arndt & Haenel 2006, pp. 175, 205.
- ↑ Borwein, Jonathan M. (2014). "The life of π: from Archimedes to ENIAC and beyond". En Sidoli, Nathan; Van Brummelen, Glen. From Alexandria, through Baghdad: Surveys and studies in the ancient Greek and medieval Islamic mathematical sciences in honor of J. L. Berggren. Heidelberg: Springer. pp. 531–561. MR 3203895. doi:10.1007/978-3-642-36736-6_24.
- ↑ Arndt & Haenel 2006, p. 171.
- ↑ Arndt & Haenel 2006, p. 176.
- ↑ Boyer & Merzbach 1991, p. 168.
- ↑ Arndt & Haenel 2006, pp. 15–16, 175, 184–186, 205. Grienberger acadou 39 díxitos en 1630; Sharp 71 díxitos en 1699.
- ↑ Arndt & Haenel 2006, pp. 176–177.
- ↑ 15,0 15,1 Boyer & Merzbach 1991, p. 202
- ↑ Arndt & Haenel 2006, p. 177.
- ↑ Arndt & Haenel 2006, p. 178.
- ↑ Arndt & Haenel 2006, p. 179.
- ↑ 19,0 19,1 Arndt & Haenel 2006, p. 180.
- ↑ Azarian, Mohammad K. (2010). "al-Risāla al-muhītīyya: A Summary". Missouri Journal of Mathematical Sciences 22 (2). pp. 64–85. doi:10.35834/mjms/1312233136.
- ↑ O'Connor, John J.; Robertson, Edmund F. (1999). "Ghiyath al-Din Jamshid Mas'ud al-Kashi". MacTutor History of Mathematics archive. Arquivado dende o orixinal o 12 de abril de 2011. Consultado o 22 de febreiro do 2023.
- ↑ 22,0 22,1 22,2 Arndt & Haenel 2006, p. 182.
- ↑ Arndt & Haenel 2006, pp. 182–183.
- ↑ Arndt & Haenel 2006, p. 183.
- ↑ Grienbergerus, Christophorus (1630). Elementa Trigonometrica (PDF) (en latín). Arquivado dende o orixinal (PDF) o 1 de febreiro de 2014. His evaluation was 3.14159 26535 89793 23846 26433 83279 50288 4196 < π < 3.14159 26535 89793 23846 26433 83279 50288 4199.
- ↑ Brezinski, C. (2009). "Some pioneers of extrapolation methods". En Bultheel, Adhemar; Cools, Ronald. The Birth of Numerical Analysis. World Scientific. pp. 1–22. ISBN 978-981-283-625-0. doi:10.1142/9789812836267_0001.
- ↑ Yoder, Joella G. (1996). "Following in the footsteps of geometry: The mathematical world of Christiaan Huygens". De Zeventiende Eeuw 12: 83–93 – vía Digital Library for Dutch Literature.
- ↑ Arndt & Haenel 2006, pp. 185–191
- ↑ 29,0 29,1 29,2 29,3 Roy, Ranjan (1990). "The Discovery of the Series Formula for π by Leibniz, Gregory and Nilakantha" (PDF). Mathematics Magazine 63 (5). pp. 291–306. doi:10.1080/0025570X.1990.11977541. Arquivado dende o orixinal (PDF) o 14 de marzo de 2023. Consultado o 23 de febreiro de 2023.
- ↑ Arndt & Haenel 2006, pp. 185–186.
- ↑ Joseph, George Gheverghese (1991). The Crest of the Peacock: Non-European Roots of Mathematics. Princeton University Press. p. 264. ISBN 978-0-691-13526-7.
- ↑ 32,0 32,1 Arndt & Haenel 2006, p. 187.
- ↑ "Decimal expansion of Buffon's constant 2/Pi". The On-Line Encyclopedia of Integer Sequences® (OEIS®) Wiki.
- ↑ Vieta, Franciscus (1593). Variorum de rebus mathematicis responsorum VIII.
- ↑ 35,0 35,1 Arndt & Haenel 2006, p. 188. Newton quoted by Arndt.
- ↑ Horvath, Miklos (1983). "On the Leibnizian quadrature of the circle." (PDF). Annales Universitatis Scientiarum Budapestiensis (Sectio Computatorica) 4. pp. 75–83.
- ↑ 37,0 37,1 Eymard & Lafon 2004, pp. 53–54
- ↑ Arndt & Haenel 2006, p. 189.
- ↑ 39,0 39,1 Jones, William (1706). Synopsis Palmariorum Matheseos. Londres: J. Wale. pp. 243, 263.
Hai outras formas de achar as lonxitudes ou áreas de determinadas liñas curvas ou planas, que poden facilitar moito a práctica; por exemplo, no círculo, o diámetro é á circunferencia como 1 a:
Carácter salto de liña en
3.14159, &c. = π. Esta serie (entre outras para o mesmo propósito, son extraídas do mesmo principio) recibina do excelente analista, e o meu moi estimado amigo Mr. John Machin; e por medio dela, o número de Van Ceulen, o Art. 64.38. pode ser examinado con toda a facilidade e rapidez desexables.|cita=na posición 213 (Axuda)Publicado en Smith, David Eugene (1929). "William Jones: The First Use of π for the Circle Ratio". A Source Book in Mathematics. McGraw–Hill. pp. 346–347.
- ↑ Tweddle, Ian (1991). "John Machin and Robert Simson on Inverse-tangent Series for π". Archive for History of Exact Sciences 42 (1). pp. 1–14. JSTOR 41133896. doi:10.1007/BF00384331.
- ↑ Arndt & Haenel 2006, pp. 192–193.
- ↑ 42,0 42,1 Arndt & Haenel 2006, pp. 72–74
- ↑ Lehmer, D. H. (1938). "On Arccotangent Relations for π" (PDF). American Mathematical Monthly 45 (10). pp. 657–664 Published by: Mathematical Association of America. JSTOR 2302434. doi:10.1080/00029890.1938.11990873. Arquivado dende o orixinal (PDF) o 07 de marzo de 2023. Consultado o 23 de febreiro de 2023.
- ↑ Roy, Ranjan (2021) [1st ed. 2011]. Series and Products in the Development of Mathematics 1 (2 ed.). Cambridge University Press. pp. 215–216, 219–220.
Newton, Isaac (1971). Whiteside, Derek Thomas, ed. The Mathematical Papers of Isaac Newton. 4, 1674–1684. Cambridge University Press. pp. 526–653.
- ↑
Sandifer, Ed (2009). "Estimating π" (PDF). How Euler Did It. Reprinted in How Euler Did Even More. Mathematical Association of America. 2014. pp. 109–118.
Euler, Leonhard (1755). "§2.2.30". Institutiones Calculi Differentialis (en latín). Academiae Imperialis Scientiarium Petropolitanae. p. 318. E 212.
Euler, Leonhard (1798) [escrito en 1779]. "Investigatio quarundam serierum, quae ad rationem peripheriae circuli ad diametrum vero proxime definiendam maxime sunt accommodatae". Nova acta academiae scientiarum Petropolitinae 11. pp. 133–149, 167–168. E 705.
Chien-Lih, Hwang (2004). "88.38 Some Observations on the Method of Arctangents for the Calculation of π". Mathematical Gazette 88 (512). pp. 270–278. doi:10.1017/S0025557200175060.
Chien-Lih, Hwang (2005). "89.67 An elementary derivation of Euler's series for the arctangent function". Mathematical Gazette 89 (516). pp. 469–470. doi:10.1017/S0025557200178404.
- ↑ Arndt & Haenel 2006, pp. 192–196, 205.
- ↑ Arndt & Haenel 2006, pp. 194–196
- ↑ Hayes, Brian (setembro de 2014). "Pencil, Paper, and Pi". American Scientist 102 (5): 342. doi:10.1511/2014.110.342. Consultado o 19 de agosto d0 2023.
- ↑ 49,0 49,1 Borwein, J.M.; Borwein, P.B. (1988). "Ramanujan and Pi". Scientific American 256 (2). pp. 112–117. Bibcode:1988SciAm.258b.112B. doi:10.1038/scientificamerican0288-112.
Arndt & Haenel 2006, pp. 15–17, 70–72, 104, 156, 192–197, 201–202 - ↑ Arndt & Haenel 2006, pp. 69–72.
- ↑ Borwein, J.M.; Borwein, P.B.; Dilcher, K. (1989). "Pi, Euler Numbers, and Asymptotic Expansions". American Mathematical Monthly 96 (8). pp. 681–687. JSTOR 2324715. doi:10.2307/2324715. hdl:1959.13/1043679.
- ↑ Arndt & Haenel 2006, Formula 16.10, p. 223.
- ↑ Wells, David (1997). The Penguin Dictionary of Curious and Interesting Numbers (revised ed.). Penguin. p. 35. ISBN 978-0-14-026149-3.
- ↑ Posamentier & Lehmann 2004, p. 284
- ↑ Arndt & Haenel 2006, p. 5.
- ↑ Lambert, Johann, "Mémoire sur quelques propriétés remarquables des quantités transcendantes circulaires et logarithmiques", reprinted in Berggren, Borwein & Borwein 1997, pp. 129–140
- ↑ Lindemann, F. (1882). "Über die Ludolph'sche Zahl". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin 2. pp. 679–682.
- ↑ Arndt & Haenel 2006, p. 196.
- ↑ Hardy e Wright 1938 e 2000: 177 nota ao pé de páxina § 11.13-14 fai referencia á proba de Lindemann que aparece en Math. Ann. 20 (1882), 213-225.
- ↑ cf Hardy e Wright 1938 e 2000:177 nota ao pé § 11.13–14. As probas de que e e π son transcendentais atópanse nas pp. 170-176. Citan dúas fontes das probas en Landau 1927 ou Perron 1910; véxase a "Lista de libros" nas pp. 417-419 para as citas completas.
- ↑ Oughtred, William (1652). Theorematum in libris Archimedis de sphaera et cylindro declarario (en latín). Excudebat L. Lichfield, Veneunt apud T. Robinson.
δ.π :: semidiámetro. semiperiferia
- ↑ 62,0 62,1 Cajori, Florian (2007). A History of Mathematical Notations: Vol. II (en inglés). Cosimo, Inc. pp. 8–13. ISBN 978-1-60206-714-1.
a relación entre a lonxitude dun círculo e o seu diámetro representábase en forma fraccionaria mediante o uso de dúas letras ... J.A. Segner ... en 1767, representou 3.14159... por δ:π, do mesmo xeito que Oughtred máis dun século antes
- ↑ Schepler, H.C. (1950) "The Chronology of Pi" Mathematics Magazine. 23.
Part 1. Jan/Feb. (3): 165–170. doi:10.2307/3029284.
Part 2. Mar/Apr. (4): 216-228. doi:10.2307/3029832.
Part 3. May/Jun. (5): 279-283. doi:10.2307/3029000.
Véxase p. 220: William Oughtred utilizou a letra π para representar a periferia (é dicir, a circunferencia) dun círculo. - ↑ 64,0 64,1 Smith, David E. (1958). History of Mathematics (en inglés). Courier Corporation. p. 312. ISBN 978-0-486-20430-7.
- ↑ Archibald, R.C. (1921). "Historical Notes on the Relation e−(π/2) = ii". The American Mathematical Monthly 28 (3). pp. 116–121. JSTOR 2972388. doi:10.2307/2972388.
Cabe destacar que estas letras "nunca" se utilizan por separado, é dicir, π non se utiliza para "Semiperiferia".
- ↑ 66,0 66,1 66,2 66,3 Arndt & Haenel 2006, p. 166.
- ↑ Vexa, por exemplo, Oughtred, William (1648). Clavis Mathematicæ [The key to mathematics] (en latín). London: Thomas Harper. p. 69. (English translation: Oughtred, William (1694). Key of the Mathematics (en inglés). J. Salusbury.)
- ↑ Barrow, Isaac (1860). "Lecture XXIV". En Whewell, William. The mathematical works of Isaac Barrow (en latín). Harvard University. Cambridge University press. p. 381.
- ↑ Gregorius, David (1695). "Ad Reverendum Virum D. Henricum Aldrich S.T.T. Decanum Aedis Christi Oxoniae" (PDF). Philosophical Transactions (en latín) 19 (231). pp. 637–652. Bibcode:1695RSPT...19..637G. JSTOR 102382. doi:10.1098/rstl.1695.0114.
- ↑ Arndt & Haenel 2006, p. 165: A facsimile of Jones' text is in Berggren, Borwein & Borwein 1997, pp. 108–109.
- ↑ Segner, Joannes Andreas (1756). Cursus Mathematicus (en latín). Halae Magdeburgicae. p. 282. Arquivado dende o orixinal o 15 de outubro de 2017. Consultado o 15 October 2017.
- ↑ Euler, Leonhard (1727). "Tentamen explicationis phaenomenorum aeris" (PDF). Commentarii Academiae Scientiarum Imperialis Petropolitana (en latín) 2. p. 351. E007. Arquivado dende o orixinal (PDF) o 1 de abril de 2016. Consultado o 17 de xullo do 2024.
Sumatur pro ratione radii ad peripheriem, I : π
English translation by Ian Bruce Arquivado 10 de xuño de 2016 en Wayback Machine.: "π tómase para a relación entre o raio e a periferia [nótese que neste traballo, o π de Euler é o dobre de noso π.]» - ↑ Euler, Leonhard (1747). Henry, Charles, ed. Lettres inédites d'Euler à d'Alembert. Bullettino di Bibliografia e di Storia delle Scienze Matematiche e Fisiche (en francés) 19 (publicado o 1886). p. 139. E858.
Car, soit π la circonference d'un cercle, dout le rayon est = 1
Tradución ao inglés en Cajori, Florian (1913). "History of the Exponential and Logarithmic Concepts". The American Mathematical Monthly 20 (3). pp. 75–84. JSTOR 2973441. doi:10.2307/2973441.Sendo π a circunferencia (!) dun círculo de raio unitario
- ↑ Euler, Leonhard (1736). "Ch. 3 Prop. 34 Cor. 1". Mechanica sive motus scientia analytice exposita. (cum tabulis) (en latín) 1. Academiae scientiarum Petropoli. p. 113. E015.
Denotet 1 : π rationem diametri ad peripheriam
English translation by Ian Bruce Arquivado 2016-06-10 en Wayback Machine. :«Sexa 1 : π} a relación entre o diámetro e a circunferencia» - ↑ Euler, Leonhard (1707–1783) (1922). Leonhardi Euleri opera omnia. 1, Opera mathematica. Volumen VIII, Leonhardi Euleri introductio in analysin infinitorum. Tomus primus / ediderunt Adolf Krazer et Ferdinand Rudio (en latín). Lipsae: B.G. Teubneri. pp. 133–134. E101. Arquivado dende o orixinal o 16 October 2017. Consultado o 17 de xullo do 2024.
- ↑ Segner, Johann Andreas von (1761). Cursus Mathematicus: Elementorum Analyseos Infinitorum Elementorum Analyseos Infinitorvm (en latín). Renger. p. 374.
Si autem π notet peripheriam circuli, cuius diameter eſt 2
- ↑ Arndt & Haenel 2006, p. 205.
- ↑ 78,0 78,1 Arndt & Haenel 2006, p. 197.
- ↑ Reitwiesner, George (1950). "An ENIAC Determination of pi and e to 2000 Decimal Places". Mathematical Tables and Other Aids to Computation 4 (29). pp. 11–15. JSTOR 2002695. doi:10.2307/2002695.
- ↑ Nicholson, J. C.; Jeenel, J. (1955). "Some comments on a NORC Computation of π". Math. Tabl. Aids. Comp. 9 (52): 162–164. JSTOR 2002052. doi:10.2307/2002052.
- ↑ Arndt & Haenel 2006, pp. 15-17.
- ↑ Arndt & Haenel 2006, p. 131.
- ↑ Arndt & Haenel 2006, pp. 132, 140.
Véxase tamén
[editar | editar a fonte]| Wikimedia Commons ten máis contidos multimedia na categoría: Número pi |
Bibliografía
[editar | editar a fonte]- Navarro, Joaquín (2010). RBA, ed. Los secretos del número π (en castelán). Barcelona. ISBN 978-84-473-6629-3.
- Abramson, Jay (2014). Precalculus. OpenStax.
- Andrews, George E.; Askey, Richard; Roy, Ranjan (1999). Special Functions. Cambridge: University Press. ISBN 978-0-521-78988-2.
- Arndt, Jörg; Haenel, Christoph (2006). Pi Unleashed. Springer-Verlag. ISBN 978-3-540-66572-4. Consultado o 5 June 2013. English translation by Catriona and David Lischka.
- Berggren, Lennart; Borwein, Jonathan; Borwein, Peter (1997). Pi: a Source Book. Springer-Verlag. ISBN 978-0-387-20571-7.
- Boyer, Carl B.; Merzbach, Uta C. (1991). A History of Mathematics (2 ed.). Wiley. ISBN 978-0-471-54397-8.
- Bronshteĭn, Ilia; Semendiaev, K.A. (1971). A Guide Book to Mathematics. Verlag Harri Deutsch. ISBN 978-3-87144-095-3.
- Dym, H.; McKean, H. P. (1972). Fourier series and integrals. Academic Press.
- Eymard, Pierre; Lafon, Jean Pierre (2004). The Number Pi. American Mathematical Society. ISBN 978-0-8218-3246-2., English translation by Stephen Wilson.
- Martini, Horst; Montejano, Luis; Oliveros, Déborah (2019). Bodies of Constant Width: An Introduction to Convex Geometry with Applications. Birkhäuser. ISBN 978-3-030-03866-3. MR 3930585. doi:10.1007/978-3-030-03868-7.
- Posamentier, Alfred S.; Lehmann, Ingmar (2004). Pi: A Biography of the World's Most Mysterious Number. Prometheus Books. ISBN 978-1-59102-200-8.
- Remmert, Reinhold (2012). "Ch. 5 What is π?". En Heinz-Dieter Ebbinghaus; Hans Hermes; Friedrich Hirzebruch; Max Koecher; Klaus Mainzer; Jürgen Neukirch; Alexander Prestel; Reinhold Remmert. Numbers. Springer. ISBN 978-1-4612-1005-4.

