Venn-diagram: Forskjell mellom sideversjoner
m robot legger til: ro:Diagramă Venn |
m Tilbakestilte endring av 84.213.139.173 (bidrag) til siste versjon av InternetArchiveBot Tagg: Tilbakestilling |
||
| (36 mellomliggende versjoner av 27 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
''' |
Et '''venndiagram''' er i [[mengdelære]] en illustrasjon som brukes for å vise [[matematikk|matematiske]] eller [[logikk|logiske]] forbindelser mellom ulike grupper av ting (mengder). |
||
Et |
Et venndiagram viser alle de logiske forbindelsene mellom mengdene. Et [[eulerdiagram]] er liknende, men behøver ikke å vise alle forbindelsene. |
||
== Eksempler == |
== Eksempler == |
||
| Linje 7: | Linje 7: | ||
[[Fil:venn-diagram-AB.png|thumb|Mengdene A og B]] |
[[Fil:venn-diagram-AB.png|thumb|Mengdene A og B]] |
||
Den oransje sirkelen ([[mengde]] ''A'') kan representere, for eksempel, alle levende vesener som er tobeinte. Den blå sirkelen |
Den oransje sirkelen ([[mengde]] ''A'') kan representere, for eksempel, alle levende vesener som er tobeinte. Den blå sirkelen (mengde ''B'') kan representere alle levende vesener som kan fly. Det området hvor den blå og den oransje sirkelen overlapper (som kalles ''skjæringsfeltet'') inneholder alle levende vesener som både kan fly ''og'' som har to bein – for eksempel papegøyer. (Tenk deg hver enkelt type vesen som et [[punkt]] et sted i diagrammet). |
||
Mennesker og pingviner ville befunnet seg i den oransje sirkelen, i det området som ikke overlapper med den blå sirkelen. Mygg har seks bein |
Mennesker og pingviner ville befunnet seg i den oransje sirkelen, i det området som ikke overlapper med den blå sirkelen. Mygg har seks bein og flyr, så punktet for mygg ville være i den delen av den blå sirkelen som ikke overlapper med den oransje. Ting som ikke har to bein og ikke kan fly (for eksempel hvaler og klapperslanger) ville alle sammen blitt representert av punkter utenfor begge sirkler. Teknisk sett kan venndiagrammet tolkes som «forbindelsene mellom mengde ''A'' og mengde ''B'' som kan ha noen (men ikke alle) elementer felles». |
||
Det samlede arealet av mengdene ''A'' og ''B'' blir kalt ''unionen'' av mengdene ''A'' og ''B''. Unionen i dette tilfellet inneholder alle ting som enten har to bein, eller som flyr, eller begge deler. At sirklene overlapper innebærer at unionen av de to mengdene ikke er tom – at det faktisk |
Det samlede arealet av mengdene ''A'' og ''B'' blir kalt ''unionen'' av mengdene ''A'' og ''B''. Unionen i dette tilfellet inneholder alle ting som enten har to bein, eller som flyr, eller begge deler. At sirklene overlapper innebærer at unionen av de to mengdene ikke er tom – at det faktisk ''er'' vesener som er i ''både'' den oransje og den blå sirkelen. |
||
Noen ganger blir et rektangel (som kalles [[univers (matematikk)|universalmengden]]) tegnet omkring |
Noen ganger blir et rektangel (som kalles [[univers (matematikk)|universalmengden]]) tegnet omkring venndiagrammet for å vise rommet for alle mulige ting. Som tidligere nevnte ville en hval blitt representert av et punkt som ikke er i unionen, men som er i [[universet]] (av levende vesener, eller av alle ting, avhengig av hvordan man velger å definere universalmengden for akkurat det diagrammet). |
||
<gallery> |
|||
| ⚫ | |||
File:Venn0001.svg|Overlappende mengde mellom to grupper<br/><math>~A \cap B</math> |
|||
File:Venn0111.svg|Samlet mengde mellom to grupper<br /><math>~A \cup B</math> |
|||
File:Venn0110.svg|Symmetrisk forskjell mellom to grupper<math>A~\Delta~B</math> |
|||
File:Venn0010.svg|Relativ komplement av A (til venstre) i B (høyre)<br /><math>A^c \cap B~=~B \setminus A</math> |
|||
File:Venn1010.svg|Absolutt komplementering av A<br/> <math>A^c~=~U \setminus A</math> |
|||
</gallery> |
|||
| ⚫ | |||
=== Eulerdiagrammer === |
=== Eulerdiagrammer === |
||
[[Fil:venn-diagram-ABC.png|thumb|Et |
[[Fil:venn-diagram-ABC.png|thumb|Et eulerdiagram]] |
||
Eulerdiagrammer har likheter med venndiagrammer, men behøver ikke vise alle mulige forbindelser. I diagrammet til høyre er en mengde fullstendig inni en annen. La oss si at mengde ''A'' er alle de ulike typene ost som fins i verden og mengde ''B'' er alle matvareslag som fins i verden. Fra diagrammet kan du se at alle oster er matvarer, men ikke alle matvarer er oster. La oss videre ta at mengde ''C'' (la oss si alle ting laget av metall) ikke har noen elementer (medlemmer av mengden) felles med mengde ''B'', og utfra det kan vi logisk påstå at ingen matvareslag er metallting (og vice versa). Diagrammet kan tolkes som: |
|||
:Mengde ''A'' er en ekte delmengde av mengde ''B'', men mengde ''C'' har ingen elementer felles med mengde ''B''. Eller, som en [[syllogisme]] |
:Mengde ''A'' er en ekte [[delmengde]] av mengde ''B'', men mengde ''C'' har ingen elementer felles med mengde ''B''. Eller, som en [[syllogisme]] |
||
* Alle ''A''er er ''B''er |
* Alle ''A''er er ''B''er |
||
* Ingen ''C''er er ''B''r |
* Ingen ''C''er er ''B''r |
||
| Linje 27: | Linje 35: | ||
* Derfor er ingen ''A''er ''C''er. |
* Derfor er ingen ''A''er ''C''er. |
||
=== Johnston- |
=== Johnston-diagrammer === |
||
[[Fil:Venn1000.svg|thumb|Johnston-diagram for påstanden ''Hverken A eller B er sanne'']] |
[[Fil:Venn1000.svg|thumb|Johnston-diagram for påstanden ''Hverken A eller B er sanne'']] |
||
[[Johnston-diagram]] |
Et [[Johnston-diagram]] kan bli brukt for å illustrere påstander i [[proposisjonslogikk]]. Et eksempel på en slik påstand er «Hverken A eller B er sanne». Diagrammet er en visuell måte å illustrere [[sannhetstabell]]er på. Det kan være identisk utseendemessig med et venndiagram, men det representerer ikke objektmengder. |
||
===Karnaugh-kart=== |
=== Karnaugh-kart === |
||
[[Karnaugh-kart]] eller ''Veitch-diagrammer'' er en annen måte å visualisere et uttrykk i [[boolsk algebra]]. |
|||
===Peirce-diagrammer=== |
=== Peirce-diagrammer === |
||
[[Peirce-diagrammer]], utformet av [[Charles Peirce]], er utvidelser av venndiagrammer. Disse diagrammene inkluderer informasjon om eksistensielle påstander, atskillende informasjon, sannsynligheter og relasjoner. [http://plato.stanford.edu/entries/diagrams/]. |
|||
==Utvidelser til høyere antall mengder== |
== Utvidelser til høyere antall mengder == |
||
Venndiagrammer har gjerne tre mengder. Venn var oppsatt på å finne ''symmetriske figurer...elegante i seg selv'' som representerte høyere antall mengder, og han utformet et firemengdersdiagram ved bruk av [[ellipse]]r. Han ga også en konstruksjon for venndiagrammer for ''ethvert'' antall kurver, der hver ny [[kurve]] innfelles i de tidligere kurvene, begynnende med 3-sirkelsdiagrammet. |
|||
===Edwards' |
=== Edwards' venndiagrammer === |
||
{| align="right" |
{| align="right" |
||
| [[Fil:Edwards-Venn-three.png|thumb|right|Edwards' |
| [[Fil:Edwards-Venn-three.png|thumb|right|Edwards' venndiagram med tre mengder]] |
||
| [[Fil:Edwards-Venn-four.png|thumb|right|Edwards' |
| [[Fil:Edwards-Venn-four.png|thumb|right|Edwards' venndiagram med fire mengder]] |
||
|- |
|- |
||
| [[Fil:Edwards-Venn-five.png|thumb|right|Edwards' |
| [[Fil:Edwards-Venn-five.png|thumb|right|Edwards' venndiagram med fem mengder]] |
||
| [[Fil:Edwards-Venn-six.png|thumb|right|Edwards' |
| [[Fil:Edwards-Venn-six.png|thumb|right|Edwards' venndiagram med seks mengder]] |
||
|} |
|} |
||
[[A. W. F. Edwards]] ga en fin konstruksjon for høyere antall mengder som innehar enkelte symmetrier. Hans konstruksjon kan oppnås ved å projisere |
[[A. W. F. Edwards]] ga en fin konstruksjon for høyere antall mengder som innehar enkelte symmetrier. Hans konstruksjon kan oppnås ved å projisere venndiagrammet på en [[sfære]]. Tre mengder kan enkelt representeres ved å ta tre halvkuler i rette vinkler (''x''≥0, ''y''≥0 og ''z''≥0). En fjerde mengde kan representeres ved å ta kurver lik dem du finner på sømmen på en tennisball som snor seg opp og ned rundt ekvator. Den resulterende mengden kan så projiseres tilbake til planet for å gi et ''tannhjul''-diagram med økende antall tenner. Disse diagrammene ble utformet under lagingen av et [[glassmalerivindu]] til minne om Venn. |
||
===Andre diagrammer=== |
=== Andre diagrammer === |
||
Edwards' |
Edwards' venndiagrammer er topologisk ekvivalente med diagrammer utformet av [[Branko Grünbaum]] som var basert omkring [[polygon]]er som skjærer hverandre med økende antall sider. De er også 2-dimensjonale representasjoner av [[hyperkube]]r. |
||
Smith utformet liknende ''n''-mengdediagrammer ved bruk av [[sinus]]-kurver med likningen ''y''=sin(2<sup>''i''</sup>''x'')/2<sup>''i''</sup>, 0≤i≤''n''-2. |
Smith utformet liknende ''n''-mengdediagrammer ved bruk av [[Sinuskurve|sinus]]-kurver med likningen ''y''=sin(2<sup>''i''</sup>''x'')/2<sup>''i''</sup>, 0≤i≤''n''-2. |
||
Charles Lutwidge Dodgson (også kjent som [[Lewis Carroll]]) utformet et fem-mengders diagram. |
Charles Lutwidge Dodgson (også kjent som [[Lewis Carroll]]) utformet et fem-mengders diagram. |
||
==Opprinnelse== |
== Opprinnelse == |
||
[[John Venn]] var en |
[[John Venn]] var en britisk [[filosof]] og [[matematiker]] i det 19. århundre. Han introduserte venndiagrammet i 1881. |
||
Et glassmalerivindu på Caius College på [[University of Cambridge|Cambridge-universitet]] er til minne om oppfinnelsen hans. |
Et glassmalerivindu på Caius College på [[University of Cambridge|Cambridge-universitet]] er til minne om oppfinnelsen hans. |
||
== |
== Se også == |
||
| ⚫ | |||
:''Alle nettsteder er på engelsk'' |
|||
| ⚫ | |||
== Kilder == |
|||
| ⚫ | |||
* [[Ian Stewart (matematiker)|I. Stewart]] ''Another Fine Math You've Got Me Into'' 1992 kap.4 |
* [[Ian Stewart (matematiker)|I. Stewart]] ''Another Fine Math You've Got Me Into'' 1992 kap.4 |
||
* A.W.F. Edwards. ''Cogwheels of the Mind: the story of Venn diagrams'', Johns Hopkins University Press, Baltimore and London, 2004. |
* A.W.F. Edwards. ''Cogwheels of the Mind: the story of Venn diagrams'', Johns Hopkins University Press, Baltimore and London, 2004. |
||
* [http://www.logic.univie.ac.at/~thompson/papers/venn-review.pdf Anmeldelse av Cogwheels of the Mind] |
* [https://web.archive.org/web/20060622021540/http://www.logic.univie.ac.at/~thompson/papers/venn-review.pdf Anmeldelse av Cogwheels of the Mind] |
||
==Se også== |
|||
| ⚫ | |||
== Eksterne lenker == |
== Eksterne lenker == |
||
* {{Offisielle lenker}} |
|||
{{commonscat|Venn diagram}}:''Alle nettsteder er på engelsk'' |
|||
* [http://www.combinatorics.org/Surveys/ds5/VennWhatEJC.html What is a Venn diagram?], fra oversiktssiden (under). |
* [https://web.archive.org/web/20060501233805/http://www.combinatorics.org/Surveys/ds5/VennWhatEJC.html What is a Venn diagram?], fra oversiktssiden (under). |
||
* [http://www.logictutorial.com/ LogicTutorial.com] |
* [http://www.logictutorial.com/ LogicTutorial.com] {{Wayback|url=http://www.logictutorial.com/ |date=20050827013704 }} – interaktivt Johnston-diagram |
||
* [http://www.cut-the-knot.org/LewisCarroll/dunham.shtml Lewis Carroll's logiske spill – Venn vs. Euler] på [[cut-the-knot]] |
* [http://www.cut-the-knot.org/LewisCarroll/dunham.shtml Lewis Carroll's logiske spill – Venn vs. Euler] på [[cut-the-knot]] |
||
* [http://www.combinatorics.org/Surveys/ds5/VennEJC.html En oversikt over Venn-diagrammer] |
* [https://web.archive.org/web/20111011075509/http://www.combinatorics.org/Surveys/ds5/VennEJC.html En oversikt over Venn-diagrammer] |
||
* [http://www.cut-the-knot.org/LewisCarroll/Venn.shtml |
* [http://www.cut-the-knot.org/LewisCarroll/Venn.shtml Venndiagrammer] på [[cut-the-knot]] |
||
* [http://www.cut-the-knot.org/LewisCarroll/VennClick.shtml Områdeidentifisering i |
* [http://www.cut-the-knot.org/LewisCarroll/VennClick.shtml Områdeidentifisering i venndiagrammer] på [[cut-the-knot]] |
||
* [http://www.combinatorics.org/Surveys/ds5/VennJohnEJC.html Glassmalerivindu] |
* [https://web.archive.org/web/20060506050320/http://www.combinatorics.org/Surveys/ds5/VennJohnEJC.html Glassmalerivindu] |
||
=== Verktøy til å lage |
=== Verktøy til å lage venndiagrammer === |
||
* [[Microsoft PowerPoint]] |
* [[Microsoft PowerPoint]] |
||
* [http://sourceforge.net/projects/venn/ VennDiagrams] |
* [http://sourceforge.net/projects/venn/ VennDiagrams] |
||
* [http://barnyard.syr.edu/software.shtml Winvenn] |
* [http://barnyard.syr.edu/software.shtml Winvenn] {{Wayback|url=http://barnyard.syr.edu/software.shtml |date=20200321024158 }} |
||
* [http://www.cs.uvic.ca/~schow/DrawVenn/instructions.html DrawVenn] |
* [https://web.archive.org/web/20070709105601/http://www.cs.uvic.ca/~schow/DrawVenn/instructions.html DrawVenn] |
||
* [http://www.venndiagram.tk VennDiagram.tk] |
* [http://www.venndiagram.tk VennDiagram.tk] {{Wayback|url=http://www.venndiagram.tk/ |date=20111020175935 }} |
||
=== Verktøy til å lage |
=== Verktøy til å lage eulerdiagrammer === |
||
* [http://www.cs.uvic.ca/~schow/DrawEuler/instructions.html DrawEuler] |
* [https://web.archive.org/web/20070709105339/http://www.cs.uvic.ca/~schow/DrawEuler/instructions.html DrawEuler] |
||
{{Autoritetsdata}} |
|||
[[Kategori:Logikk]] |
[[Kategori:Logikk]] |
||
[[Kategori:Mengdelære]] |
[[Kategori:Mengdelære]] |
||
[[Kategori: |
[[Kategori:Statistiske diagram]] |
||
{{Link AA|es}} |
|||
[[ar:مخطط فيين]] |
|||
[[ca:Diagrama de Venn]] |
|||
[[cs:Vennův diagram]] |
|||
[[da:Venn-diagram]] |
|||
[[de:Mengendiagramm]] |
|||
[[et:Venni diagramm]] |
|||
[[en:Venn diagram]] |
|||
[[es:Diagrama de Venn]] |
|||
[[eo:Venn-a diagramo]] |
|||
[[eu:Vennen diagrama]] |
|||
[[fa:نمودار ون]] |
|||
[[fr:Diagramme de Venn]] |
|||
[[ko:벤 다이어그램]] |
|||
[[hi:वेन आरेख]] |
|||
[[io:Venn-diagramo]] |
|||
[[id:Diagram Venn]] |
|||
[[is:Venn-mynd]] |
|||
[[it:Diagramma di Eulero-Venn]] |
|||
[[he:דיאגרמת ון]] |
|||
[[lt:Veno diagrama]] |
|||
[[nl:Venn-diagram]] |
|||
[[ja:ベン図]] |
|||
[[pms:Diagrama d'Euler-Venn]] |
|||
[[pl:Diagram Venna]] |
|||
[[pt:Diagrama de Venn]] |
|||
[[ro:Diagramă Venn]] |
|||
[[ru:Круги Эйлера]] |
|||
[[sk:Vennov diagram]] |
|||
[[sl:Vennov diagram]] |
|||
[[fi:Venn-diagrammi]] |
|||
[[sv:Venndiagram]] |
|||
[[tr:Venn şeması]] |
|||
[[zh:文氏图]] |
|||
Siste sideversjon per 16. sep. 2024 kl. 10:58
Et venndiagram er i mengdelære en illustrasjon som brukes for å vise matematiske eller logiske forbindelser mellom ulike grupper av ting (mengder).
Et venndiagram viser alle de logiske forbindelsene mellom mengdene. Et eulerdiagram er liknende, men behøver ikke å vise alle forbindelsene.
Eksempler
[rediger | rediger kilde]
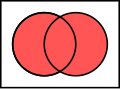
Den oransje sirkelen (mengde A) kan representere, for eksempel, alle levende vesener som er tobeinte. Den blå sirkelen (mengde B) kan representere alle levende vesener som kan fly. Det området hvor den blå og den oransje sirkelen overlapper (som kalles skjæringsfeltet) inneholder alle levende vesener som både kan fly og som har to bein – for eksempel papegøyer. (Tenk deg hver enkelt type vesen som et punkt et sted i diagrammet).
Mennesker og pingviner ville befunnet seg i den oransje sirkelen, i det området som ikke overlapper med den blå sirkelen. Mygg har seks bein og flyr, så punktet for mygg ville være i den delen av den blå sirkelen som ikke overlapper med den oransje. Ting som ikke har to bein og ikke kan fly (for eksempel hvaler og klapperslanger) ville alle sammen blitt representert av punkter utenfor begge sirkler. Teknisk sett kan venndiagrammet tolkes som «forbindelsene mellom mengde A og mengde B som kan ha noen (men ikke alle) elementer felles».
Det samlede arealet av mengdene A og B blir kalt unionen av mengdene A og B. Unionen i dette tilfellet inneholder alle ting som enten har to bein, eller som flyr, eller begge deler. At sirklene overlapper innebærer at unionen av de to mengdene ikke er tom – at det faktisk er vesener som er i både den oransje og den blå sirkelen.
Noen ganger blir et rektangel (som kalles universalmengden) tegnet omkring venndiagrammet for å vise rommet for alle mulige ting. Som tidligere nevnte ville en hval blitt representert av et punkt som ikke er i unionen, men som er i universet (av levende vesener, eller av alle ting, avhengig av hvordan man velger å definere universalmengden for akkurat det diagrammet).
-
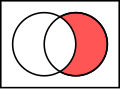
Overlappende mengde mellom to grupper
-
Samlet mengde mellom to grupper
-
Symmetrisk forskjell mellom to grupper
-
Relativ komplement av A (til venstre) i B (høyre)
-
Absolutt komplementering av A
Liknende diagrammer
[rediger | rediger kilde]Eulerdiagrammer
[rediger | rediger kilde]
Eulerdiagrammer har likheter med venndiagrammer, men behøver ikke vise alle mulige forbindelser. I diagrammet til høyre er en mengde fullstendig inni en annen. La oss si at mengde A er alle de ulike typene ost som fins i verden og mengde B er alle matvareslag som fins i verden. Fra diagrammet kan du se at alle oster er matvarer, men ikke alle matvarer er oster. La oss videre ta at mengde C (la oss si alle ting laget av metall) ikke har noen elementer (medlemmer av mengden) felles med mengde B, og utfra det kan vi logisk påstå at ingen matvareslag er metallting (og vice versa). Diagrammet kan tolkes som:
- Mengde A er en ekte delmengde av mengde B, men mengde C har ingen elementer felles med mengde B. Eller, som en syllogisme
- Alle Aer er Ber
- Ingen Cer er Br
- Derfor er ingen Cer Aer.
- Derfor er ingen Aer Cer.
Johnston-diagrammer
[rediger | rediger kilde]
Et Johnston-diagram kan bli brukt for å illustrere påstander i proposisjonslogikk. Et eksempel på en slik påstand er «Hverken A eller B er sanne». Diagrammet er en visuell måte å illustrere sannhetstabeller på. Det kan være identisk utseendemessig med et venndiagram, men det representerer ikke objektmengder.
Karnaugh-kart
[rediger | rediger kilde]Karnaugh-kart eller Veitch-diagrammer er en annen måte å visualisere et uttrykk i boolsk algebra.
Peirce-diagrammer
[rediger | rediger kilde]Peirce-diagrammer, utformet av Charles Peirce, er utvidelser av venndiagrammer. Disse diagrammene inkluderer informasjon om eksistensielle påstander, atskillende informasjon, sannsynligheter og relasjoner. [1].
Utvidelser til høyere antall mengder
[rediger | rediger kilde]Venndiagrammer har gjerne tre mengder. Venn var oppsatt på å finne symmetriske figurer...elegante i seg selv som representerte høyere antall mengder, og han utformet et firemengdersdiagram ved bruk av ellipser. Han ga også en konstruksjon for venndiagrammer for ethvert antall kurver, der hver ny kurve innfelles i de tidligere kurvene, begynnende med 3-sirkelsdiagrammet.
Edwards' venndiagrammer
[rediger | rediger kilde] |
 |
 |
 |
A. W. F. Edwards ga en fin konstruksjon for høyere antall mengder som innehar enkelte symmetrier. Hans konstruksjon kan oppnås ved å projisere venndiagrammet på en sfære. Tre mengder kan enkelt representeres ved å ta tre halvkuler i rette vinkler (x≥0, y≥0 og z≥0). En fjerde mengde kan representeres ved å ta kurver lik dem du finner på sømmen på en tennisball som snor seg opp og ned rundt ekvator. Den resulterende mengden kan så projiseres tilbake til planet for å gi et tannhjul-diagram med økende antall tenner. Disse diagrammene ble utformet under lagingen av et glassmalerivindu til minne om Venn.
Andre diagrammer
[rediger | rediger kilde]Edwards' venndiagrammer er topologisk ekvivalente med diagrammer utformet av Branko Grünbaum som var basert omkring polygoner som skjærer hverandre med økende antall sider. De er også 2-dimensjonale representasjoner av hyperkuber.
Smith utformet liknende n-mengdediagrammer ved bruk av sinus-kurver med likningen y=sin(2ix)/2i, 0≤i≤n-2.
Charles Lutwidge Dodgson (også kjent som Lewis Carroll) utformet et fem-mengders diagram.
Opprinnelse
[rediger | rediger kilde]John Venn var en britisk filosof og matematiker i det 19. århundre. Han introduserte venndiagrammet i 1881.
Et glassmalerivindu på Caius College på Cambridge-universitet er til minne om oppfinnelsen hans.
Se også
[rediger | rediger kilde]Kilder
[rediger | rediger kilde]- A Survey of Venn Diagrams av F. Ruskey og M. Weston, er et omfattende nettsted med mye nyere forskning og mange vakre figurer.
- I. Stewart Another Fine Math You've Got Me Into 1992 kap.4
- A.W.F. Edwards. Cogwheels of the Mind: the story of Venn diagrams, Johns Hopkins University Press, Baltimore and London, 2004.
- Anmeldelse av Cogwheels of the Mind
Eksterne lenker
[rediger | rediger kilde]- (en) Venn diagrams – kategori av bilder, video eller lyd på Commons
- What is a Venn diagram?, fra oversiktssiden (under).
- LogicTutorial.com Arkivert 27. august 2005 hos Wayback Machine. – interaktivt Johnston-diagram
- Lewis Carroll's logiske spill – Venn vs. Euler på cut-the-knot
- En oversikt over Venn-diagrammer
- Venndiagrammer på cut-the-knot
- Områdeidentifisering i venndiagrammer på cut-the-knot
- Glassmalerivindu
Verktøy til å lage venndiagrammer
[rediger | rediger kilde]- Microsoft PowerPoint
- VennDiagrams
- Winvenn Arkivert 21. mars 2020 hos Wayback Machine.
- DrawVenn
- VennDiagram.tk Arkivert 20. oktober 2011 hos Wayback Machine.