Kubooktaeder
| Kubooktaeder | |
|---|---|
 (animacija) | |
| vrsta | arhimedsko telo uniformni polieder |
| elementi | F = 14, E = 24, V = 12 (χ = 2) |
| stranske ploskve na stran | 8{3} + 6{4} |
| Conwayjev zapis | aC aaT |
| Schläflijevi simboli | rr{4,3} ali rr{3,3} ali |
| t1{4,3} ali t0,2{3,3} | |
| Wythoffov simbol | 2 | 3 4 3 3 | 2 |
| Coxeter-Dinkinov diagram | |
| simetrija | Oh, B3, [4,3], (*432), red 48 Td, [3,3], (*332), red 24 |
| vrtilna grupa | O, [4,3]+, (432), red 24 |
| diedrski kot | 125,26° |
| sklici | U07, C19, W11 |
| značilnosti | konveksen polpravilen kvazipravilen |
 obarvane stranske ploskve |
 3.4.3.4 (slika oglišč) |
 rombski dodekaeder (dualni polieder) |
 mreža telesa |
Kubooktaeder je v geometriji konveksni polieder. Je arhimedsko telo, eno od trinajstih konveksnih izogonalnih neprizmatičnih teles skonstruirano z dvema ali več vrstami pravilnih mnogokotniških stranskih ploskev.
Ima štirinajst pravilnih stranskih ploskev, od tega osem enakostraničnotrikotniških in šest kvadratnih. Ima 24 popolnoma skladnih robov, ki vsak ločuje enakostranični trikotnik od kvadrata, ter 12 popolnoma enakih oglišč, v katerih se stikajo dva enakostranična trikotnika in dva kvadrata. Zaradi tega je polpravilni polieder, ki je tako ogliščno kot robovnoprehoden.
Njegov dualni polieder, oziroma Catalanovo telo, je rombski dodekaeder.
Telo je bilo verjetno znano Platonu. V Heronovih Definitiones je naveden Arhimed, ki naj bi izrekel, da je Platon vedel za telo sestavljeno iz 8-ih trikotnikov in 6-ih kvadratov.[1]
Druga imena
[uredi | uredi kodo]- heptaparaleloeder (Buckminster Fuller)
- Fuller je uporabil ime »dimaksion« za to obliko, uporabljeno v zgodnejši različici dimaksionske projekcije. Imenoval ga je tudi »vektorsko ravnovesje.«[2] Kubooktaeder sestavljen iz togih opornikov povezanih z gibljivimi oglišči je imenoval »jitterbug« (ta oblika se lahko deformira v oktaeder, tetraeder ali ikozaeder z odstranjenjem kvadratnih ploskev).
- s simetrijo Oh reda 48 je rektificirana kocka ali rektificirani oktaeder (Norman Johnson)
- s simetrijo Td reda 24 je kantelirani tetraeder ali rombitetraeder.
- s simetrijo D3d reda 12 je trikotniška girobikupola.
Kartezične koordinate
[uredi | uredi kodo]Kartezične koordinate 12 oglišč kubooktaedra s središčem v izhodišču z dolžino robu enako so:
- (±1, ±1, 0)
- (±1, 0, ±1)
- (0, ±1, ±1)
Alternativna množica koordinat obstaja v 4-prostoru kot 12 permutacij:
- (0, 1, 1, 2)
Ta konstrukcija obstaja kot ena od 16-ih ortantnih facet kantelirane 16-celice.
Korenski vektorji
[uredi | uredi kodo]12 oglišč kubooktaedra lahko predstavlja korenske vektorje enostavne Liejeve grupe A3. Z dodatnimi 6-imi oglišči oktaedra ta oglišča predstavljajo 18 korenskih vektorjev enostavne Liejeve grupe B3.
Površina in prostornina
[uredi | uredi kodo]Površina P in prostornina V kubooktaedra z dolžino robu a sta:
Če se skonstruira množica vseh 13-ih arhimedskih teles z enakimi dolžinami robov, bi bil kubooktaeder najmanjši.
Pravokotne projekcije
[uredi | uredi kodo]Kubooktaeder ima štiri posebne pravokotne projekcije usrediščene na oglišče, rob in dve vrsti stranskih ploskev (enakostranični trikotniki in kvadrati). Zadnji dve odgovarjata Coxeterjevima ravninama B2 in A2. Poševni projekciji kažeta kvadrat in šestkotnik, ki potekata skozi središče kubooktaedra.
| usrediščeno na | oglišče |
rob |
stransko ploskev – kvadrat |
stransko ploskev – enakostranični trikotnik |
poševni projekciji | |
|---|---|---|---|---|---|---|
| slika | 
|

|

|

|

|

|
| projektivna simetrija |
[2] | [2] | [4] | [6] | ||
| rombski dodekaeder |

|

|
|

|

|

|
Sferno tlakovanje
[uredi | uredi kodo]Kubooktaeder se lahko predstavi tudi kot sferno tlakovanje in projicira na ravnino s stereografsko projekcijo. Ta projekcija je konformna in ohranja kote ne pa tudi ploščin ali dolžin. Premice na sferi se projicirajo kot krožni loki na ravnino.
| ortografska projekcija | stereografski projekciji | |
|---|---|---|

|

|

|
| usrediščeno na kvadrat | usrediščeno na enakostranični trikotnik | |
Disekcija
[uredi | uredi kodo]Kubooktaeder se lahko razdeli na dve trikotniški kupoli s skupnim šestkotnikom, ki poteka skozi središče kubooktaedra. Če se ti dve trikotniški kupoli zavrtita tako, da se med seboj poravnajo trikotniki in kvadrati, nastane Johnsonovo telo J27, trikotniška ortobikupola, ki se imenuje tudi antikubooktaeder.
Kubooktaeder se lahko razdeli tudi na 6 kvadratnih piramid in 8 tetraedrov, ki se srečajo v središču. Ta disekcija je izražena v alterniranem kubičnem satovju, kjer so pari kvadratnih piramid kombinirani v oktaedre.
Geometrijski odnosi
[uredi | uredi kodo]

Kubooktaeder lahko nastane z ustreznim presekom štirirazsežne 16-celice.
Kubooktaeder ima oktaedrsko simetrijo. Njegova prva stelacija je sestav kocke in njenega duala oktaedra, kjer oglišča kubooktaedra ležijo na razpoloviščih robov obeh teles.
Kubooktaeder je rektificirana kocka in tudi rektificirani oktaeder.
Je tudi kantelirani tetraeder. S to konstrukcijo je dan Wythoffov simbol: 3 3 | 2. 
Poševna kantelacija tetraedra tvori telo s stranskimi ploskvami vzporednimi s stranskimi ploskvami kubooktaedra, osem tikotnikov dveh velikosti in šest pravokotnikov. Njegovi robovi sicer niso enaki, ostaja pa točkovnoprehoden: ima polno tetraedrsko simetrijsko grupo in njegova oglišča so pod njo enakovredna.
RObovi kubooktaedra tvorijo pravilni šestkotnik. Če se oktaeder preseka v ravnini enega od teh šestkotnikov, vsaka nastala polovica predstavlja trikotniško kupolo, enega od Johnsonovih teles J3. Zaradi tega se lahko kubooktaeder imenuje tudi trikotniška girobikupola, najpreprostejša v nizu (poleg girobifastigija ali »diagonalne girobikupole«). Če se polovici zavrtita tako, da se med seboj poravnajo trikotniki in kvadrati, in nazaj spojita, nastane novo Johnsonovo telo, J27, trikotniška ortobikupola, imenovana tudi antikubooktaeder.
Obe trikotniški bikupoli sta pomembni pri pakiranju krogel. Razdalja med središčem telesa do njegovih oglišč je enaka dolžini robov. Vsaka središčna krogla ima lahko do dvanajst sosedov, in v ploskovnocentrirani kubični mreži ti lahko zavzamejo lege oglišč kubooktaedra. V šeskotniški gostopakirani mreži odgovarjajo ogliščem trikotniške ortobikupole. V obeh primerih središčna krogla leži v središču telesa.
Kubooktaedri se pojavljajo kot celice v treh konveksnih uniformnih satovjih in v devetih uniformnih polihoronih.
Prostornina kubooktaedra je 5/6 ograjene kocke in 5/8 ograjenega oktaedra.
Razvrstitev oglišč
[uredi | uredi kodo]Kubooktaeder ima enako razvrstitev robov in oglišč kot dva nekonveksna uniformna poliedra: kubohemioktaeder (skupne kvadratne stranske ploskve) in oktahemioktaeder (skupne trikotniške stranske ploskve). Velja tudi kot kantelirani tetraeder kot rektificirani tetratetraeder.
 kubooktaeder |
 kubohemioktaeder |
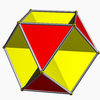 oktahemioktaeder |
Kubooktaeder 2-pokrije tetrahemiheksaeder,[3] ki ima temu ustrezno enako abstraktno sliko oglišč (dva trikotnika in dva kvadrata: 3.4.3.4) in polovico oglišč, robov in stranskih ploskev. (Dejanska slika oglišč tetrahemiheksaedra je 3.4.3/2.4, s faktorjem a/2 zaradi križa.)
 kubooktaeder |
 tetrahemiheksaeder |
Sorodni poliedri
[uredi | uredi kodo]Kubooktaeder predstavlja eno družino uniformnih poliedrov povezanih s kocko in pravilnim oktoedrom.
| Družina uniformnih oktaedrskih poliedrov | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Simetrija: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
||||||||
| Duali uniformnih poliedrov | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
Kubooktaeder ima tudi tetraedrsko simetrijo z dvema barvama trikotnikov.
| Družina uniformnih tetraedrskih poliedrov | |||||||
|---|---|---|---|---|---|---|---|
| Simetrija: [3,3], (*332) | [3,3]+, (332) | ||||||

|

|

|

|

| |||
| {3,3} | t{3,3} | r{3,3} | t{3,3} | {3,3} | rr{3,3} | tr{3,3} | sr{3,3} |
| Duali uniformnih poliedrov | |||||||

|

|

|

| ||||
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
Sorodni kvazipravilni poliedri in tlakovanja
[uredi | uredi kodo]Kubooktaeder obstaja v zaporedju simetrij kvazipravilnih poliedrov in tlakovanj s konfiguracijami oglišč (3.n)2, od tlakovanja sfere do evklidske ravnine v hiperbolično ravnino. Z orrbiteričnim zapisom simetrije *n32 so vsa ta tlakovanja Wythoffova konstrukcija znotraj fundamentalne domene simetrije, z generatorskimi točkami ob oglišču domene s pravim kotom.[4][5]
| Orbiterične simetrije *n32 kvazipravilnih tlakovanj: (3.n)2 | |||||||
|---|---|---|---|---|---|---|---|
konstrukcija |
sferna | evklidska | hiperbolična | ||||
| *332 | *432 | *532 | *632 | *732 | *832... | *∞32 | |
| kvazipravilne oblike |

|

|

|

|

|

|

|
| oglišče | (3.3)2 | (3.4)2 | (3.5)2 | (3.6)2 | (3.7)2 | (3.8)2 | (3.∞)2 |
| Različice simetrij *n42 kvazipravilnih tlakovanj: (4.n)2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| simetrija *4n2 [n,4] |
sferna | evklidska | kompaktna hiperbolična | parakompaktna | nekompaktna | |||
| *342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] |
[ni,4] | |
| slika | 
|

|

|

|

|

|

|
|
| oglišče | (4.3)2 | (4.4)2 | (4.5)2 | (4.6)2 | (4.7)2 | (4.8)2 | (4.∞)2 | (4.ni)2 |
Ta polieder je topološko povezan kot del niza kanteliranih poliedrov s sliko oglišč (3.4.n.4) in se nadaljuje kot tlakovanje hiperbolične ravnine. Te ogliščnoprehodne oblike imajo zrcalno simetrijo (*n32).
| Različice simetrij *n32 razširjenih tlakovanj: 3.4.n.4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| simetrija *n32 [n,3] |
sferna | evklidska | kompaktna hiperb. | parakomp. | ||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] | |
| slika | 
|

|

|

|

|

|

|

|
| konfig. | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4.∞.4 |
Sorodni politopi
[uredi | uredi kodo]
Kubooktaeder se lahko razstavi v pravilni oktaeder in osem nepravilnih vendar skladnih oktaedrov v obliki konveksne ogrinjače kocke z dvema nasprotnima ogliščema odstranjenima. Ta dekompozicija kubooktaedra odgovarja projekciji v tri razsežnosti 24-celice vzporedni s prvo celico. Pod to projekcijo kubooktaeder tvori projekcijsko ogrinjačo, ki se lahko razstavi v šest kvadratnih stranskih ploskev, pravilni oktaeder in osem nepravilnih oktaedrov. Ti elementi odgovarjajo slikam šestim oktaedrskim celicam v 24-celici, najbližji in najbolj oddaljene celice iz štirirazsežnega pogleda in preostalih osem parov celic.
Pojavitev v kulturi in medijih
[uredi | uredi kodo]- v epizodi »By Any Other Name« druge sezone Zvezdnih stez tuja bitja napadejo vesoljsko ladjo Enterprise in pretvorijo posadko v nežive kubooktaedre.
- igrača »Geo Twister« [1] Arhivirano 2007-08-06 na Wayback Machine. je elastični kubooktaeder.
- vesoljske postaje Coriolis v računalniški igri Elite imajo obliko kubooktaedra.
Glej tudi
[uredi | uredi kodo]Sklici
[uredi | uredi kodo]- ↑ Heath (1931), str. 176.
- ↑ Fuller, R. Buckminster. »Vector Equilibrium« (v angleščini).
- ↑ Richter, David A., Two Models of the Real Projective Plane (v angleščini), arhivirano iz prvotnega spletišča dne 3. marca 2016, pridobljeno 27. junija 2016
{{citation}}: Vzdrževanje CS1: ref podvaja privzeto (povezava) - ↑ Coxeter (1973).
- ↑ Huson (1991).
Viri
[uredi | uredi kodo]- Coxeter, Harold Scott MacDonald (1973), »§ V: The Kaleidoscope, Section: 5.7 Wythoff's construction«, Regular Polytopes (3. izd.), Dover, ISBN 0-486-61480-8
- Heath, Thomas Little (1931), A manual of Greek mathematics, Clarendon
- Huson, Daniel H. (1991), Two Dimensional symmetry Mutations
Nadaljnje branje
[uredi | uredi kodo]- Cromwell, Peter Richard (1997), »Archimedean solids«, Polyhedra, Cambridge, New York: Cambridge University Press, str. 79–86, COBISS 6472537, ISBN 0-521-55432-2
- Ghyka, Matila (1977), The geometry of art and life. ([Nachdr.] izd.), New York: Dover Publications, str. 51–56, 81–84, ISBN 9780486235424
- Weisstein, Eric Wolfgang (2002). »Cuboctahedron«. CRC Concise Encyclopedia of Mathematics (2. izd.). Hoboken: CRC Press. str. 620–621. ISBN 9781420035223.
- Williams, Robert Edward (1979), »Section 3-9«, The Geometrical Foundation of Natural Structure: A Source Book of Design, Dover Publications, Inc, ISBN 0-486-23729-X
Zunanje povezave
[uredi | uredi kodo]- Weisstein, Eric Wolfgang. »Cuboctahedron«. MathWorld.
- Weisstein, Eric Wolfgang. »Archimedean Solid«. MathWorld.
- The Uniform Polyhedra (angleško)
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra (angleško)
- Klitzing, Richard, 3D convex uniform polyhedra, o3x4o - co (angleško)
- Editable printable net of a Cuboctahedron with interactive 3D view (angleško)






