இருசமபக்க முக்கோணம்

இருசமபக்க முக்கோணம்
சமச்சீர் குத்தச்சுகொண்ட இருசமபக்க முக்கோணம்
வகை	முக்கோணம்
விளிம்புகள் மற்றும் உச்சிகள்	3
சிலாஃப்லி குறியீடு	( ) ∨ { }
சமச்சீர் குலம்	Dih2, [ ], (*), வரிசை 2
இருமப் பல்கோணம்	தன்-இருமை
பண்புகள்	குவிவு, சுழல் பல்கோண வகை

வடிவவியலில் இருசமபக்க முக்கோணம் (isosceles triangle) என்பது மூன்று பக்கங்களில் எவையேனும் இரண்டு பக்கங்கள் சமநீளமுள்ளவையாகக் கொண்ட முக்கோணமாகும். ஒரு முக்கோணம் இருசமபக்க முக்கோணமாக இருப்பதற்கு அதன் இரண்டு பக்கங்கள் மட்டும் சமநீளமானவையாக இருந்தால் போதுமானது. முக்கோணத்தின் மூன்று பக்கங்களும் சமநீளமானவையாக இருந்தால் அம்முக்கோணம் சமபக்க முக்கோணம் ஆகும். எனவே இருசமபக்க முக்கோணத்தின் சிறப்புவகையாக, சமபக்க முக்கோணத்தக் கருதலாம்.

இருசமபக்க முக்கோணத் தேற்றத்தின்படி, ஒரு இருசமபக்க முக்கோணத்தில் சமபக்கங்கள் இரண்டிற்கும் எதிரே அமையும் இரு கோணங்களின் அளவுகளும் சமமாகும். ஸ்டெயினர்-லெமசு தேற்றத்தின்படி, முக்கோணத்தின் இரண்டு கோண இருசமவெட்டிகள் சமநீளமுள்ளவையாக இருந்தால், அம்முக்கோணமானது இருசமபக்க முக்கோணமாக இருக்கும்.

சொல்லியல்

இரண்டு பக்கங்கள் மட்டும் சமமானவையாக உள்ள இருசமபக்க முக்கோணத்தில், அச்சமபக்கங்கள் இரண்டும் ’தாங்கிகள்’ அல்லது ’தாங்கு பக்கங்கள்’ எனவும், மூன்றாவது பக்கம் அடிப்பக்கம் எனவும் அழைக்கப்படும். தாங்கு பக்ககளுக்கிடையே அமையும் கோணம் ”உச்சிக்கோணம்” என்றும் அடிப்பக்கத்தை ஒரு கரமாகக் கொண்ட கோணங்கள் இரண்டும் ”அடிக்கோணங்கள்” என்றும் அழைக்கப்படுகின்றன..

இரண்டு பக்கங்களை மட்டும் சமமானவையாகக் கொண்ட முக்கோணமென யூக்ளிடும், குறைந்தபட்சம் இரண்டு பக்கங்கள் சமமானவையென தற்கால வரையறைகளும் இருசமபக்க முக்கோணத்தை வரையறுக்கின்றன குறைந்தபட்சம் இரண்டு பக்கங்கள் சமமானவையாகக் கொண்டது என்ற வரையறையின்படி, மூன்று பக்கங்களும் சமமாகவுள்ள சமபக்க முக்கோணமானது, இருசமபக்க முக்கோணத்தின் ஒரு சிறப்புவகையாக அமைகிறது. மேலும் சமபக்க முக்கோணத்தில் எந்தவொரு பக்கத்தையும் அடிப்பக்கமாகக் கொள்ளலாம்; தாங்கிகள் என எந்தப்பக்கமும் அழைக்கப்படுவதில்லை.

சமச்சீர்மை

இரண்டு சமப்பக்கங்கள் மட்டும் கொண்ட இருசமபக்க முக்கோணத்திற்கு ஒரு சமச்சீர் அச்சு உள்ளது. இந்த சமச்சீர் அச்சு முக்கோணத்தின் உச்சிக்கோணத்தின் வழியாகவும் அடிப்பக்கத்தின் நடுப்புள்ளி வழியாகவும் செல்லும்.

எனவே சமச்சீர் அச்சானது, உச்சிக்கோணத்தின் இருசமவெட்டி, அடிப்பக்கத்தின் நடுக்கோடு, குத்துக்கோடு, அடிப்பக்கத்தின் நடுக்குத்துக்கோடு ஆகிய நான்குடனும் ஒன்றுபடும்

குறுங்கோண, செங்கோண, விரிகோண முக்கோணம்

ஒரு இருசமபக்க முக்கோணத்தின் உச்சிக்கோணத்தின் அளவைப் பொறுத்துதான் அம்முக்கோணமானது விரிகோண/செங்கோண/குறுங்கோண முக்கோணமாக அமையும். யூக்ளிடிய வடிவவியலில் ஒரு முக்கோணத்தின் மூன்று கோணங்களின் கூடுதல் 180° என்பதால், ஒரு இருசமபக்க முக்கோணத்தின் அடிக்கோணங்கள் விரிகோணங்களாகவோ (>90°) அல்லது செங்கோணங்களாகவோ (90°) இருக்க முடியாது.

ஒரு முக்கோணத்தின் ஏதேனுமொரு கோணம் விரிகோணம்/செங்கோணமாக இருந்தால், இருந்தால் மட்டுமே, அம்முக்கோணம் விரிகோண/செங்கோண முக்கோணமாகும். அதேபோல ஒரு இருசமபக்க முக்கோணத்தின் உச்சிக்கோணமானது குறுங்கோணம்/ செங்கோணம்/விரிகோணமாக இருந்தால், இருந்தால் மட்டுமே, அம்முக்கோணம் இருசமபக்க விரிகோண முக்கோணம்/இருசமபக்க செங்கோண முக்கோணம்/இருசமபக்க குறுங்கோண முக்கோணமாகும்.

ஆய்லர் கோடு

ஒரு முக்கோணத்தின் நடுக்கோட்டுச் சந்தி, செங்குத்துச்சந்தி, சுற்றுவட்ட மையம் ஆகிய மூன்று புள்ளிகளும் ஆய்லர் கோட்டின் மீது அமையும்.

இரண்டு பக்கங்களை மட்டும் சமமாகக்கொண்ட இருசமபக்க முக்கோணத்தில் அதன் சமச்சீர் அச்சும் ஆய்லர் கோடும் ஒன்றாகும்:

இருசமபக்க முக்கோணத்தின் அடிப்பக்கத்தின் குத்துக்கோடு, நடுக்கோடு, பக்க நடுக்குத்துக்கோடு மூன்றும் அதன் சமச்சீர் அச்சாகவே இருக்கும். என்பதால், அம்முக்கோணத்தின் நடுக்கோட்டுச்சந்தி, செங்குத்துச்சந்தி, சுற்றுவட்ட மையம் மூன்றும் அச்சமச்சீர் அச்சிலேயே அமைகின்றன. எனவே இந்த இருசமபக்க முக்கோணத்தில், சமச்சீர் அச்சுதான் ஆய்லரின் கோடாக உள்ளது.

உச்சிக்கோணம் குறுங்கோணமாக உள்ள இருசமபக்க முக்கோணத்தின் செங்குத்துச்சந்தி, நடுக்கோட்டுச்சந்தி, சுற்றுவட்ட மையம் மூன்றும் முக்கோணத்தின் உட்புறத்திலும், உச்சிக்கோணம் விரிகோணமாகவுள்ள இருசமபக்க முக்கோணத்தின் நடுக்கோட்டுச்சந்தி முக்கோணத்தின் உட்புறத்திலும், சுற்றுவட்ட மையம் முக்கோணத்தின் வெளிப்புறத்திலும் அமைகின்றன. இருசமபக்க முக்கோணத்தின் உள்வட்டமையம் அம்முக்கோணத்தின் ஆய்லர் கோட்டின் மீதமையும்.

ஸ்டெயினர் உள்நீள்வட்டம்

ஒரு முக்கோணத்தின் பக்கங்களை அவற்றின் நடுப்புள்ளிகளை முக்கோணத்தின் உட்புறமைமாகத் தொட்டவாறுள்ள நீள்வட்டம் ஸ்டெயினர் உள்நீள்வட்டமாகும்.

ஒரு இருசமப்பக்க முக்கோணத்தின் தாங்கு பக்கங்கள் அதன் அடிப்பக்கத்தைவிட நீளமானதாக இருந்தால், அம்முக்கோணத்தின் ஸ்டெயினர் உள்நீள்வட்டத்தின் நெட்டச்சானது முக்கோணத்தின் சமச்சீர் அச்சுடன் ஒன்றுபடும். மாறாக, இருசமப்பக்க முக்கோணத்தின் தாங்கு பக்கங்கள் அதன் அடிப்பக்கத்தைவிட சிறியனவாக இருந்தால், அம்முக்கோணத்தின் ஸ்டெயினர் உள்நீள்வட்டத்தின் சிற்றச்சானது முக்கோணத்தின் சமச்சீர் அச்சுடன் ஒன்றுபடும்.

வாய்ப்பாடுகள்

இருசமபக்க முக்கோணத்தின் சமபக்கங்களின் நீளம் a ; அடிப்பக்க நீளம் b.

1. உச்சிக்கோண இருசமவெட்டியின் நீளம் (முக்கோணத்தின் உட்புறமுள்ள நீளம்)
2. அடிப்பக்கத்திற்கு வரையப்பட்ட நடுக்கோட்டின் நீளம்
3. அடிப்பக்கத்திற்கு வரையப்பட்ட குத்துக்கோட்டின்நீளம்
4. அடிப்பக்கத்தின் நடுக்குத்துக்கோட்டின் நீளம் (முக்கோணத்தின் உட்புறமுள்ள நீளம்)

இந்நான்கும் கீழ்க்காணும் ஒரே வாய்ப்பாடால் பெறப்படுகின்றன:

${\tfrac {1}{2}}{\sqrt {4a^{2}-b^{2}}}.$

T -பரப்பளவும், p -சுற்றளவும் கொண்ட இருசமபக்க முக்கோணத்திற்கு கீழ்வரும் முடிவு உண்மையாக இருக்கும்.

$2pb^{3}-p^{2}b^{2}+16T^{2}=0.$

பரப்பளவு

முக்கோணத்தின் பரப்பளவு காணப் பயன்படும் ஈரோனின் வாய்பாடு:

$T={\sqrt {s(s-a)(s-b)(s-c)}},$

முக்கோணத்தின் பக்க நீளங்கள்: a, b, c அரைச்சுற்றளவு:

$s={\frac {a+b+c}{2}}.$

இவ்வாய்பாட்டினை கீழுள்ளவாறு மாற்றியமைக்கலாம்:

$T={\frac {1}{4}}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}$

$T={\frac {1}{4}}{\sqrt {2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})}}$

$T={\frac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}$

$T={\frac {1}{4}}{\sqrt {4a^{2}b^{2}-(a^{2}+b^{2}-c^{2})^{2}}}.$

இருசமபக்க முக்கோணத்தின் இரு பக்கங்கள் சமமென்பதால் மேலுள்ள வாய்ப்பாட்டில் a = c எனப் பதிலிடக் கிடைப்பது:

$T={\frac {1}{4}}{\sqrt {4a^{2}b^{2}-(a^{2}+b^{2}-a^{2})^{2}}}.$

$T={\frac {1}{4}}{\sqrt {4a^{2}b^{2}-b^{4}}}.$

$T={\frac {b}{4}}{\sqrt {4a^{2}-b^{2}}}.$

பித்தாகரசு தேற்றத்தினைப் பயன்படுத்தியும் இருசமபக்க முக்கோணத்தின் பரப்பளவு காணலாம்.

இருசமபக்க முக்கோணம்

இருசமபக்க முக்கோணத்தின் அடிப்பக்கம் b , செங்குத்துயரம் h , தாங்குபக்க நீளம் a.

பித்தாகரசின் தேற்றப்படி,

$(b/2)^{2}+h^{2}=a^{2}$

$h={\frac {\sqrt {4a^{2}-b^{2}}}{2}}$

முக்கோணத்தின் பரப்பளவு:

$T={\frac {1}{2}}\times bh$

இதில் h இன் மதிப்பைப் பதிலிட:

$T={\frac {b}{4}}{\sqrt {4a^{2}-b^{2}}}.$

இருசமக்க முக்கோணம் அதன் செங்குத்துயரத்தால் இரு சர்வசம செங்கோண முக்கோணங்களாகக் பிரிக்கப்படுகிறது. இருசமபக்க முக்கோணத்தின் உச்சிக்கோணம் (θ) எனில் இந்த இரு செங்கோண முக்கோணங்களின்

அடிப்பக்க நீளம்:

$a\sin({\frac {\theta }{2}})$

செங்குத்துயரம்:

$a\cos({\frac {\theta }{2}})$

ஒரு செங்கோணமுக்கோணத்தின் பரப்பளவு:

$T={\frac {1}{2}}a\sin \left({\frac {\theta }{2}}\right)a\cos \left({\frac {\theta }{2}}\right)$

எனவே இருசமபக்க முக்கோணத்தின் பரப்பளவு:

$T=a^{2}\sin \left({\frac {\theta }{2}}\right)\cos \left({\frac {\theta }{2}}\right)$

sin(θ) = 2sin(θ/2)cos(θ/2) என்ற வாய்பாடைப் பயன்படுத்த:

$T={\frac {1}{2}}a^{2}\sin \theta$

இருசமபக்க முக்கோணங்களாகப் பிரித்தல்

n ≥ 4 எனில் எந்தவொரு முக்கோணத்தையும் n இருசமபக்க முக்கோணங்களாகப் பிரிக்கமுடியும்.

ஒரு செங்கோண முக்கோணத்தின் செம்பக்கத்தின் நடுக்கோடு, அந்த முக்கோணத்தை இரண்டு இருசமபக்க முக்கோணங்களாகப் பிரிக்கிறது:

ஏனென்றால், செம்பக்கத்தின் நடுப்புள்ளி செங்கோண முக்கோணத்தின் சுற்றுவட்ட மையமாகும். மேலும் செம்பக்கத்தின் நடுக்கோட்டின் பிரிப்பால் கிடைக்கப்பெற்ற இரண்டு முக்கோணங்களும் சுற்றுவட்ட ஆரத்தை இரு பக்கங்களாகக் கொண்டிருக்கும். எனவே அவை இருசமபக்க முக்கோணங்களாக உள்ளன.

ஒரு குறுங்கோண தங்க முக்கோணமாகவும் மற்றொரு விரிகோண தங்க முக்கோணமாகவும் (golden gnomon) பிரிக்கப்பட்டதொரு தங்க முக்கோணம்.

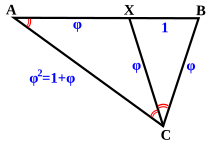
தங்க முக்கோணம் ஒரு இருசமபக்க முக்கோணம் ஆகும். அதன் சமபக்க நீளத்திற்கும் அடிப்பக்க நீளத்திற்குமுள்ள விகிதம் தங்க விகிதமாக ($\varphi ={1+{\sqrt {5}} \over 2}.$) இருக்கும். மேலும் இம்முக்கோணத்தின் கோணங்கள் 72°, 72°, 36° ஆகவும் அவற்றின் விகிதம் 2:2:1 உள்ளது.

தங்க முக்கோணத்தை இரண்டு இருசமபக்க முக்கோணங்களாகப் பிரிக்கலாம். ஒரு குறுங்கோண தங்க முக்கோணமாகவும் மற்றொரு விரிகோண தங்க முக்கோணமாகவும் (golden gnomon) பிரிக்கலாம். இந்த விரிகோண இருசமபக்க முக்கோணத்தின் அடிப்பக்கத்திற்கும் தாங்குபக்கத்திற்குமான விகிதம் பொன்விகிதமாக இருக்கும். மேலும் இதன் கோணங்கள் 36°, 36°, 108° ; இவற்றின் விகிதம் 1:1:3 ஆகும்.

ஏனைய விவரங்கள்

ஒரு முப்படிச் சமன்பாட்டிற்கு இரு சிக்கலெண் தீர்வுகளும் ஒரு மெய்யெண் தீர்வும் கொண்டிருக்கும்போது அத்தீர்வுகளை சிக்கலெண் தளத்தில் குறித்தால் அவை ஒரு இருசமபக்க முக்கோணத்தின் உச்சிகளாக அமைகின்றன. சிக்கலெண் தீர்வுகள் இரண்டும் ஒன்றுக்கொன்று இணையியங்களாகும். எனவே முக்கோணமானது மெய்யச்சைப் பொறுத்து சமச்சீராக இருக்கும். அதாவது முக்கோணத்தின் சமச்சீர் அச்சானது சிக்கலெண் தளத்தின் மெய்யச்சுடன் ஒன்றுபடும்.

ஒரு சாய்சதுரத்தின் இரு மூலைவிட்டங்களும் சாய்சதுரத்தை இரு சர்வசம இருசமபக்க முக்கோணங்களாகப் பிரிக்கும்.

மேற்கோள்கள்

• Heath, Thomas L. (1956), The Thirteen Books of Euclid's Elements, vol. 1 (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] ed.), New York: Dover Publications, பன்னாட்டுத் தரப்புத்தக எண் 0-486-60088-2
• Jacobs, Harold R. (1974), Geometry, W. H. Freeman and Co., பன்னாட்டுத் தரப்புத்தக எண் 0-7167-0456-0
• Ostermann, Alexander; Wanner, Gerhard (2012), Geometry by Its History, Springer, பன்னாட்டுத் தரப்புத்தக எண் 978-3-642-29162-3
• Stahl, Saul (2003), Geometry from Euclid to Knots, Prentice-Hall, பன்னாட்டுத் தரப்புத்தக எண் 0-13-032927-4
• Venema, Gerard A. (2006), Foundations of Geometry, Prentice-Hall, பன்னாட்டுத் தரப்புத்தக எண் 0-13-143700-3