ZDD入門-お姉さんを救う方法
- 1. ZDD入門 (副題:お姉さんを救う方法) 西尾 泰和 1
- 2. お姉さん? • 副題の元ネタがわからない人は Youtubeで「フカシギの数え方」を見てください http://www.youtube.com/watch?v=Q4gTV4r0zRs 2
- 3. 前回のあらすじ • 前回のランダムフォレスト(竹迫さん)は 決定木を「特徴をランダムに選んで、決 定しきらなくても適当に打ち切って、と にかくたくさん作って多数決!」だった • 今回も決定木だが「特徴を全部使って、 巨大な決定木をつくるぞ!」という話 3
- 4. 決定木が表現するもの • 0/1の特徴がたくさん与えられて0/1を返す関数 • 具体例: • 論理式(項が特徴、式の値が返り値) • 部分集合の族(各頂点が部分集合xに含まれる かどうかが特徴、その部分集合が族に含まれ るかどうかが返り値) 4
- 5. もっと具体例 の族 この情報を どうやって コンピュータの中に 表現する? 5
- 6. vector<bool> • ←赤枠の中身を持つ • 特徴の個数をNとして2^N bitのメモリ 3×3 は辺が12本 → 4096通り → 512バイト → 余裕! 6
- 7. 5×5だと? • 辺の本数は4×5×2=40本 • 局面数は2^40 = 1テラ通り • 必要なメモリは128ギガバイト… 7
- 8. もう一声!6×6! • 辺の本数は5×6×2=60本 • 局面数は2^60 = 1ゼタ通り • 必要なメモリは128エクサバイト… 一億テラバイト以上?! お姉さん死んじゃう!やめて! 8
- 9. 解のvectorで持つ xyzr 0000 • 「全部1bit使うよりf(x)=1が成立するx 0010 だけリストアップすればいいのでは」 0100 0111 • 6×6だと一局面を60bitで表現できる 1000 1011 • 解の個数は126万2816通り 1101 1111 • 60bit × 1262816 ≒ 9メガバイト • これならメモリに収まる! 9
- 10. もう二声!8×8! • 辺の本数は 7×8×2=112本 • 一局面に 112bit • 解の個数:789ギガ通り • 112bit × 789ギガ通り ≒ 11テラバイト お姉さん死んじゃう!やめて! 10
- 11. どうすればいい?? 11
- 12. 共通部分をまとめる • 「?」の部分がなんであれ結果は同一 →じゃあ別個に持つ必要ないじゃん! →共通部分をまとめて圧縮しよう! 12
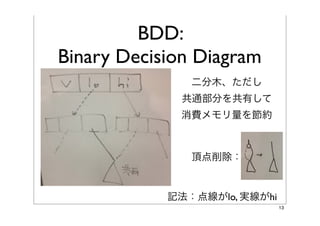
- 13. BDD: Binary Decision Diagram 二分木、ただし 共通部分を共有して 消費メモリ量を節約 頂点削除: 記法:点線がlo, 実線がhi 13
- 14. さらに • スタートから横に進む辺を選んだら、 下に進む辺を選んではいけない。 選んだらその後どうあがいても全部NG → 「?」の中身がどうでも 全部NGになる 14
- 15. ZDD: Zero-supress BDD • BDDとちょっと頂点削除のルールが違う • ZDD:「ここが1だったらどうやっても 結果が0になる」な頂点を削除 • BDD:「ここが0でも1でも結果が変わら ない」な頂点を削除 ←違いはわずか 15
- 16. ZDDで8×8! • ZDDで表現した場合の頂点数:33580個 • 112辺のどの辺についての頂点かを識別す るために8bit使おう (7bitでも足りるけど) • 33580個の頂点を識別するには16bit必要 • (8bit + 16bit × 2) × 33580 ≒ 168キロバイト 11テラ→168キロ!! TAOCP-ja 7.1 P121 16
- 17. BDD/ZDDで何が出来る? • 168KBで 789ギガ通りの解の集合を保持できる • 解を辞書順に列挙できる • 全ての解が等確率なサンプリングが出来る • ある局面がOKかNGか、 最大112ステップで判定できる • BDDのまま和・積などの集合演算ができる 17
- 18. 何が出来る? 続き(2/4) • f(x)→0/1 のBDDがあると、 与えられた重みベクトルwについて、 f(x) = 1の条件下で内積wxを最大化する解xを O(n+B)ステップで求められる(Boole計画法) • 例えば各辺のコストが与えられたら、 コスト最小のパスを探せる n: xのビット数、B: BDDの頂点数 18
- 19. 何が出来る? 続き(3/4) * 独立に • 各x_iが確率p_iで1になる時*に、 f(x) = 1である確率をO(B)ステップで 求められる(信頼性多項式) 0.1 * 0.2 * (1-0.3) * (1-0.4) + (1-0.1) * (1-0.2) * 0.3 * 0.4 B: BDDの頂点数 19
- 20. 何が出来る? 続き(4/4) • f(x) = 1の解の個数を最悪実行時間O(nB)で 求めることが出来る • 例えばお姉さんが救える! n: fのビット数、B: BDDの頂点数 20
- 21. そんな便利なBDDを どうすれば作れるか? 21
- 22. to be continued... 22