Travelling Salesman Problem (Greedy Approach)

The travelling salesman problem is a graph computational problem where the salesman needs to visit all cities (represented using nodes in a graph) in a list just once and the distances (represented using edges in the graph) between all these cities are known. The solution that is needed to be found for this problem is the shortest possible route in which the salesman visits all the cities and returns to the origin city.

If you look at the graph below, considering that the salesman starts from the vertex a, they need to travel through all the remaining vertices b, c, d, e, f and get back to a while making sure that the cost taken is minimum.

There are various approaches to find the solution to the travelling salesman problem: naive approach, greedy approach, dynamic programming approach, etc. In this tutorial we will be learning about solving travelling salesman problem using greedy approach.

Travelling Salesperson Algorithm

As the definition for greedy approach states, we need to find the best optimal solution locally to figure out the global optimal solution. The inputs taken by the algorithm are the graph G {V, E}, where V is the set of vertices and E is the set of edges. The shortest path of graph G starting from one vertex returning to the same vertex is obtained as the output.

Algorithm

• Travelling salesman problem takes a graph G {V, E} as an input and declare another graph as the output (say G) which will record the path the salesman is going to take from one node to another.

• The algorithm begins by sorting all the edges in the input graph G from the least distance to the largest distance.

• The first edge selected is the edge with least distance, and one of the two vertices (say A and B) being the origin node (say A).

• Then among the adjacent edges of the node other than the origin node (B), find the least cost edge and add it onto the output graph.

• Continue the process with further nodes making sure there are no cycles in the output graph and the path reaches back to the origin node A.

• However, if the origin is mentioned in the given problem, then the solution must always start from that node only. Let us look at some example problems to understand this better.

Examples

Consider the following graph with six cities and the distances between them −

From the given graph, since the origin is already mentioned, the solution must always start from that node. Among the edges leading from A, A → B has the shortest distance.

Then, B → C has the shortest and only edge between, therefore it is included in the output graph.

Theres only one edge between C → D, therefore it is added to the output graph.

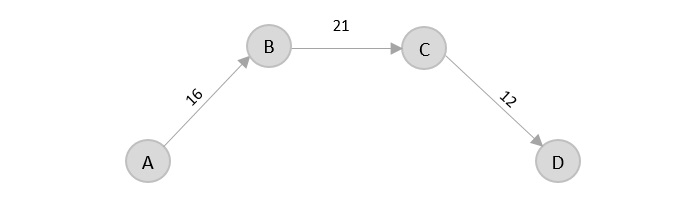
Theres two outward edges from D. Even though, D → B has lower distance than D → E, B is already visited once and it would form a cycle if added to the output graph. Therefore, D → E is added into the output graph.

Theres only one edge from e, that is E → F. Therefore, it is added into the output graph.

Again, even though F → C has lower distance than F → A, F → A is added into the output graph in order to avoid the cycle that would form and C is already visited once.

The shortest path that originates and ends at A is A → B → C → D → E → F → A

The cost of the path is: 16 + 21 + 12 + 15 + 16 + 34 = 114.

Even though, the cost of path could be decreased if it originates from other nodes but the question is not raised with respect to that.

Example

The complete implementation of Travelling Salesman Problem using Greedy Approach is given below −

#include <stdio.h>
int tsp_g[10][10] = {
   {12, 30, 33, 10, 45},
   {56, 22, 9, 15, 18},
   {29, 13, 8, 5, 12},
   {33, 28, 16, 10, 3},
   {1, 4, 30, 24, 20}
};
int visited[10], n, cost = 0;

/* creating a function to generate the shortest path */
void travellingsalesman(int c){
   int k, adj_vertex = 999;
   int min = 999;
   
   /* marking the vertices visited in an assigned array */
   visited[c] = 1;
   
   /* displaying the shortest path */
   printf("%d ", c + 1);
   
   /* checking the minimum cost edge in the graph */
   for(k = 0; k < n; k++) {
      if((tsp_g[c][k] != 0) && (visited[k] == 0)) {
         if(tsp_g[c][k] < min) {
            min = tsp_g[c][k];
            adj_vertex = k;
         }
      }
   }
   if(min != 999) {
      cost = cost + min;
   }
   if(adj_vertex == 999) {
      adj_vertex = 0;
      printf("%d", adj_vertex + 1);
      cost = cost + tsp_g[c][adj_vertex];
      return;
   }
   travellingsalesman(adj_vertex);
}

/* main function */
int main(){
   int i, j;
   n = 5;
   for(i = 0; i < n; i++) {
      visited[i] = 0;
   }
   printf("Shortest Path: ");
   travellingsalesman(0);
   printf("\nMinimum Cost: ");
   printf("%d\n", cost);
   return 0;
}

Shortest Path: 1 4 5 2 3 1
Minimum Cost: 55

#include <iostream>
using namespace std;
int tsp_g[10][10] = {{12, 30, 33, 10, 45},
{56, 22, 9, 15, 18},
{29, 13, 8, 5, 12},
{33, 28, 16, 10, 3},
{1, 4, 30, 24, 20}
};
int visited[10], n, cost = 0;

/* creating a function to generate the shortest path */
void travellingsalesman(int c){
   int k, adj_vertex = 999;
   int min = 999;
   
   /* marking the vertices visited in an assigned array */
   visited[c] = 1;
   
   /* displaying the shortest path */
   cout<<c + 1<<" ";
   
   /* checking the minimum cost edge in the graph */
   for(k = 0; k < n; k++) {
      if((tsp_g[c][k] != 0) && (visited[k] == 0)) {
         if(tsp_g[c][k] < min) {
            min = tsp_g[c][k];
               adj_vertex = k;
         }
      }
   }
   if(min != 999) {
      cost = cost + min;
   }
   if(adj_vertex == 999) {
      adj_vertex = 0;
      cout<<adj_vertex + 1;
      cost = cost + tsp_g[c][adj_vertex];
      return;
   }
   travellingsalesman(adj_vertex);
}

/* main function */
int main(){
   int i, j;
   n = 5;
   for(i = 0; i < n; i++) {
      visited[i] = 0;
   }
   cout<<"Shortest Path: ";
   travellingsalesman(0);
   cout<<"\nMinimum Cost: ";
   cout<<cost;
   return 0;
}

Shortest Path: 1 4 5 2 3 1
Minimum Cost: 55

import java.util.*;
public class Main {
    static int[][] tsp_g = {
	   {12, 30, 33, 10, 45},
       {56, 22, 9, 15, 18},
       {29, 13, 8, 5, 12},
       {33, 28, 16, 10, 3},
       {1, 4, 30, 24, 20}};
    static int[] visited;
    static int n, cost;
    public static void travellingsalesman(int c) {
        int k, adj_vertex = 999;
        int min = 999;
        visited[c] = 1;
        System.out.print((c + 1) + " ");
        for (k = 0; k < n; k++) {
            if ((tsp_g[c][k] != 0) && (visited[k] == 0)) {
                if (tsp_g[c][k] < min) {
                    min = tsp_g[c][k];
					adj_vertex = k;
                }
            }
        }
        if (min != 999) {
            cost = cost + min;
        }
        if (adj_vertex == 999) {
            adj_vertex = 0;
            System.out.print((adj_vertex + 1));
            cost = cost + tsp_g[c][adj_vertex];
            return;
        }
        travellingsalesman(adj_vertex);
    }
    public static void main(String[] args) {
        int i, j;
        n = 5;
        visited = new int[n];
        Arrays.fill(visited, 0);
        System.out.print("Shortest Path: ");
        travellingsalesman(0);
        System.out.print("\nMinimum Cost: ");
        System.out.print(cost);
    }
}

Shortest Path: 1 4 5 2 3 1
Minimum Cost: 55

import numpy as np
def travellingsalesman(c):
    global cost
    adj_vertex = 999
    min_val = 999
    visited[c] = 1
    print((c + 1), end=" ")
    for k in range(n):
        if (tsp_g[c][k] != 0) and (visited[k] == 0):
            if tsp_g[c][k] < min_val:
                min_val = tsp_g[c][k]
                adj_vertex = k
    if min_val != 999:
        cost = cost + min_val
    if adj_vertex == 999:
        adj_vertex = 0
        print((adj_vertex + 1), end=" ")
        cost = cost + tsp_g[c][adj_vertex]
        return
    travellingsalesman(adj_vertex)
n = 5
cost = 0
visited = np.zeros(n, dtype=int)
tsp_g = np.array([[12, 30, 33, 10, 45],
                  [56, 22, 9, 15, 18],
                  [29, 13, 8, 5, 12],
                  [33, 28, 16, 10, 3],
                  [1, 4, 30, 24, 20]])
print("Shortest Path:", end=" ")
travellingsalesman(0)
print()
print("Minimum Cost:", end=" ")
print(cost)

Shortest Path: 1 4 5 2 3 1 
Minimum Cost: 55