无字证明

无字证明（英語：proof without words）是指仅用图像而无需文字解释就能不证自明的数学命题。由于其不证自明的特性，这种证明方式被认为比严格的数学证明更为优雅与有条理。^[1]无字证明通常只是用图像来说明一个证明中的特例，因而需要推广才能构成完整的证明。^[2]

示例

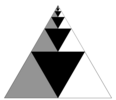
从1至2n-1之间的所有奇数之和为平方数n²的无字证明如右图所示。^[3]第一个正方形由一个方块组成，即1为首个平方数。之后增加3个白色方块以组成第二个正方形，总共有4个方块，即4为第二个平方数。之后再增加5个黑色方块组成下一个平方数9，并以此类推。

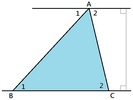
勾股定理可以由右边第二张图（出自《周髀算经》）进行证明。通过两种不同的方法计算大的正方形的面积可以得到

a^{2}+b^{2}=c^{2}\,

虽然没有上一个例子那么明显，但也可以看作是无字证明。^[4]

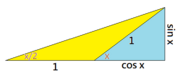
延森不等式可由右边第三张图加以证明。沿X轴的点曲线为X的假想分布，沿Y轴的点曲线则为相应的Y的分布。可以看到随着X值的增大，凸映射Y(X)使得分布不断地“延长”。^[5]

無字證明範例

證明 $\tan {\frac {x}{2}}={\frac {\sin x}{1+\cos x}}$ ，其中 $0<x<90^{\circ }$
證明二元算幾不等式 ${\frac {a+b}{2}}\geq {\sqrt {ab}}{}$ ^[6]
證明二元算幾不等式 ${\frac {a+b}{2}}\geq {\sqrt {ab}}{}$ ^[6]
證明在歐氏幾何中，任意三角形內角和為180°
證明無窮等比級數 ${\frac {1}{4}}+{\frac {1}{16}}+{\frac {1}{64}}+\cdots ={\frac {1}{3}}$

^ Dunham 1994，第120頁
^ Weisstein, Eric W. (编). Proof without Words. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）. Retrieved on 2008-6-20
^ Dunham 1994，第121頁
^ Nelsen 1997，第3頁
^ Jensen's Inequality, Bulletin of the American Mathematical Society 43 (8) (American Mathematical Society), 1937, 43 (8): 527
^ ^6.0 ^6.1 周伯欣. 二元算幾不等式的一個無字證明一一附記一段學思歷程 (PDF). 數學傳播: 35-38頁. （原始内容存档 (PDF)于2024-09-01）（中文（臺灣））.

Dunham, William, The Mathematical Universe, John Wiley and Sons, 1974, ISBN 0-471-53656-3
Nelsen, Roger B., Proofs without Words: Exercises in Visual Thinking, Mathematical Association of America: 160, 1997, ISBN 978-0-88385-700-7
Nelsen, Roger B., Proofs without Words II: More Exercises in Visual Thinking, Mathematical Association of America: 142, 2000, ISBN 0-88385-721-9