Matemática: diferenças entre revisões
m Foram revertidas as edições de Loury123 devido a vandalismo (usando Huggle) (3.4.12) |
+ ampliação Etiqueta: Inserção de predefinição obsoleta |
||
| Linha 1: | Linha 1: | ||
{{mais fontes|ciência=sim|data=fevereiro de 2012}} |
|||
[[Imagem:Egyptian A'h-mosè or Rhind Papyrus (1065x1330).png|thumb|[[Papiro de Rhind]], um documento antigo contendo [[Problema matemático|problemas matemáticos]]]] |
|||
{{Ciências-vertical}} |
{{Ciências-vertical}} |
||
'''Matemática''' é uma área do [[conhecimento]] que inclui os tópicos dos [[números]], [[Fórmula (lógica)|fórmulas]] e estruturas relacionadas, formas e os espaços em que estão contidos, e quantidades e suas mudanças. Esses tópicos são representados na matemática moderna com as principais subdisciplinas da [[teoria dos números]],<ref name="OED">{{Citar web|url=https://www.oed.com/dictionary/mathematics_n?tab=meaning_and_use&tl=true|titulo=Mathematics (noun)|acessodata=17 de janeiro de 2024|website=[[Oxford English Dictionary]]|publicado=[[Oxford University Press]]}}</ref> [[álgebra]],<ref name="Kneebone">{{Citar livro|título=Mathematical Logic and the Foundations of Mathematics: An Introductory Survey|ultimo=Kneebone|primeiro=G. T.|editora=D. Van Nostard Company|ano=1963|capitulo=Traditional Logic|lccn=62019535|mr=0150021|oclc=792731}}</ref> [[geometria]]<ref name="OED" /> e [[Análise matemática|análise]],<ref name="LaTorre">{{Citar livro|título=Calculus Concepts: An Applied Approach to the Mathematics of Change|ultimo=LaTorre|primeiro=Donald R.|ultimo2=Kenelly|primeiro2=John W.|ultimo3=Reed|primeiro3=Iris B.|ultimo4=Carpenter|primeiro4=Laurel R.|ultimo5=Harris|primeiro5=Cynthia R.|ultimo6=Biggers|editora=[[Houghton Mifflin Company]]|ano=2008|capitulo=Models and Functions|isbn=978-0-618-78983-2|lccn=2006935429|oclc=125397884|edição=4th}}</ref> respectivamente. No entanto, não há consenso entre os matemáticos sobre uma definição comum para a [[Disciplina (conhecimento)|disciplina acadêmica]] que estudam. |
|||
'''Matemática''' (dos termos [[Língua grega|gregos]]: ''[[wikt:μάθημα|μάθημα]]'', [[transliteração|transliterado]] ''máthēma'', '[[ciência]]', [[conhecimento]]' ou '[[aprendizagem]]<ref>{{citar web|url=http://www.etimo.it/?term=matematica&find|titulo=Matematica, Mattematica|publicado=Vocabolario Etimologico della Lingua Italiana|ultimo=Pianigiani|primeiro=Ottorino|língua=it|acessodata=6 de Abril de 2016}}</ref>; e ''[[wikt:μαθηματικός|μαθηματικός]]'', transliterado ''mathēmatikós'', 'inclinado a aprender') é a [[ciência]] do [[raciocínio lógico]] e [[Abstração|abstrato]], que estuda [[quantidade]]s ([[teoria dos números]]), espaço e medidas ([[geometria]]), [[Topologia (matemática)|estruturas]], [[Cálculo|variações]]<ref>{{citar livro|url=https://books.google.com/books?id=XCRC6BeKhIIC&pg=SA2–PA10|título=Applied Mathematics|ultimo=Ramana|editora=Tata McGraw–Hill Education|ano=2007|página=2.10|isbn=978-0-07-066753-2|citacao=The mathematical study of change, motion, growth or decay is calculus.}}</ref> e [[estatística]].<ref>{{citar web |url=http://oed.com/view/Entry/114974 |titulo=mathematics, ''n.'' |data=2012 |acessodata=17 de julho de 2021 |website=Oxford English Dictionary |publicado=Oxford University Press |arquivourl=https://web.archive.org/web/20191116075558/https://www.oed.com/view/Entry/114974 |arquivodata=16 de novembro de 2019 |urlmorta=Não |citacao=The science of space, number, quantity, and arrangement, whose methods involve logical reasoning and usually the use of symbolic notation, and which includes geometry, arithmetic, algebra, and analysis.}}</ref><ref>{{citar livro|url=https://books.google.com/books?id=tCXxf4vbXCcC&pg=PA4|título=Mathematical Logic and the Foundations of Mathematics: An Introductory Survey|ultimo=Kneebone|primeiro=G.T.|editora=Dover|ano=1963|página=4|isbn=978-0-486-41712-7|citacao=Mathematics ... is simply the study of abstract structures, or formal patterns of connectedness.}}</ref><ref>{{citar livro|url=https://books.google.com/books?id=9TATfteVeVYC&pg=PR7|título=An Invitation to Mathematics: From Competitions to Research|ultimo=Ziegler|primeiro=Günter M.|editora=Springer|página=vii|capitulo=What Is Mathematics?|isbn=978-3-642-19532-7}}</ref> Não há, porém, uma definição consensual por parte da comunidade científica.<ref>{{citar periódico |titulo=Images of Mathematics Held by University Teachers of Mathematical Sciences |data=dezembro de 1993 |jornal=Educational Studies in Mathematics |número=4 |ultimo=Mura |primeiro=Roberta |paginas=375–385 |doi=10.1007/BF01273907 |jstor=3482762 |volume=25}}</ref><ref>{{citar livro|url=https://books.google.com/books?id=EDm0eQqFUQ4C&pg=PA9|título=Iris Runge: A Life at the Crossroads of Mathematics, Science, and Industry|ultimo=Tobies|primeiro=Renate|ultimo2=Neunzert|primeiro2=Helmut|editora=Springer|ano=2012|página=9|isbn=978-3-0348-0229-1|citacao=[I]t is first necessary to ask what is meant by ''mathematics'' in general. Illustrious scholars have debated this matter until they were blue in the face, and yet no consensus has been reached about whether mathematics is a natural science, a branch of the humanities, or an art form.}}</ref> O trabalho matemático consiste em procurar e relacionar padrões,<ref>{{citar periódico |url=https://www.ascd.org/publications/curriculum-handbook/409/chapters/the-future-of-mathematics-education.aspx |titulo=The Science of Patterns |data=29 de abril de 1988 |acessodata=18 de julho de 2021 |jornal=Science |número=240 |ultimo=Steen |primeiro=Lynn .A. |paginas=611-616 |arquivourl=https://web.archive.org/web/20101028101034/http://www.ascd.org/publications/curriculum-handbook/409/chapters/The-Future-of-Mathematics-Education.aspx |arquivodata=28 de outubro de 2010 |resumo-url=http://www.ascd.org/publications/curriculum-handbook/409/chapters/The-Future-of-Mathematics-Education.aspx |resumo-fonte=Association for Supervision and Curriculum Development}}</ref><ref>{{citar livro|título=Mathematics: The Science of Patterns: The Search for Order in Life, Mind and the Universe|ultimo=Devlin|primeiro=Keith|editora=Scientific American Paperback Library|ano=1996|isbn=978-0-7167-5047-5}}</ref> de modo a formular [[conjectura]]s<ref>{{citar periódico |url=https://revistas.rcaap.pt/index.php/quadrante/article/download/22881/16947/88229 |titulo=Os padrões e o raciocínio indutivo em matemática |data=2012 |acessodata=18 de julho de 2021 |jornal=Quadrante |número=2 |ultimo=Pimentel |primeiro=Teresa |ultimo2=Vale |primeiro2=Isabel |volume=XXI}}</ref> cuja veracidade ou falsidade é [[Prova matemática|provada]] por meio de [[Dedução|deduções]] rigorosas, a partir de [[axioma]]s e definições. A matemática desenvolveu-se principalmente na [[Mesopotâmia]], no [[Egito]], na [[Grécia]], na [[Índia]] e no [[Oriente Médio]]. Após a [[Renascença]], o desenvolvimento da matemática intensificou-se na [[Europa]], quando novas descobertas científicas levaram a um acúmulo rápido de conhecimento que dura até os dias de hoje.<ref>{{citar livro|título=Introdução à História da Matemática|ultimo=Mol|primeiro=Rogério Santos|editora=CAED-UFMG|ano=2013|local=Belo Horizonte|isbn=978-85-64724-26-6|acessodata=27 de março de 2017}}</ref> |
|||
Grande parte da atividade matemática envolve a descoberta de propriedades de [[Objeto matemático|objetos abstratos]] e o uso da [[razão]] pura para [[Prova matemática|prová-las]]. Estes objetos consistem em [[Abstração (matemática)|abstrações]] da natureza ou {{Mdash}} segundo a [[matemática moderna]] {{Mdash}} entidades que são estipuladas por certas propriedades, chamadas [[Axioma|axiomas]]. Uma ''[[prova matemática]]'' consiste em uma sucessão de aplicações de [[Regra de inferência|regras dedutivas]] a resultados já estabelecidos. Estes resultados incluem [[Teorema|teoremas]] previamente provados, axiomas e {{Mdash}} no caso de abstração da natureza {{Mdash}} algumas propriedades básicas que são consideradas pontos de partida da teoria em consideração.<ref>{{Citar livro|url=https://www.alws.at/alws/wp-content/uploads/2018/06/papers-2015.pdf#page=133|título=Realismus – Relativismus – Konstruktivismus: Beiträge des 38. Internationalen Wittgenstein Symposiums|ultimo=Hipólito|primeiro=Inês Viegas|data=15 de agosto de 2015|editora=Austrian Ludwig Wittgenstein Society|editor-sobrenome=Kanzian|volume=23|localização=Kirchberg am Wechsel, Austria|páginas=132–134|língua=de, en|capitulo=Abstract Cognition and the Nature of Mathematical Proof|issn=1022-3398|oclc=236026294|acessodata=17 de janeiro de 2024|editor-sobrenome2=Mitterer|editor-link2=Josef Mitterer|editor-sobrenome3=Neges|arquivourl=https://web.archive.org/web/20221107221937/https://www.alws.at/alws/wp-content/uploads/2018/06/papers-2015.pdf#page=133|arquivodata=7 de novembro de 2022}} ([https://www.researchgate.net/publication/280654540_Abstract_Cognition_and_the_Nature_of_Mathematical_Proof at ResearchGate] {{Acesso aberto}} {{Webarchive|url=https://web.archive.org/web/20221105145638/https://www.researchgate.net/publication/280654540_Abstract_Cognition_and_the_Nature_of_Mathematical_Proof|date=5 de novembro de 2022}})</ref> |
|||
Registros [[arqueologia|arqueológicos]] mostram que a matemática é tanto um fator [[cultura]]l quanto parte da história do desenvolvimento da [[Homo sapiens|espécie humana]]. Ela evoluiu por meio de contagens, medições, cálculos e do estudo [[sistema|sistemático]] de formas geométricas e movimentos de objetos físicos. |
|||
A matemática é essencial nas [[ciências naturais]], [[engenharia]], [[medicina]], [[finanças]], [[Ciência da computação|ciências da computação]] e [[ciências sociais]]. Embora seja amplamente utilizada para modelar fenômenos, as verdades fundamentais da matemática são independentes de qualquer [[experimentação]] científica. Algumas [[áreas da matemática]], como [[estatística]] e [[teoria dos jogos]], são desenvolvidas em estreita correlação com suas aplicações e, portanto, são frequentemente agrupadas na [[matemática aplicada]]. Outros campos de estudo são desenvolvidos independentemente de qualquer aplicação (e por este motivo são chamados de [[matemática pura]]), mas muitas vezes encontram aplicações práticas posteriormente.{{Sfn|Peterson|1988|p=12}}<ref name="wigner1960">{{Citar periódico |url=https://math.dartmouth.edu/~matc/MathDrama/reading/Wigner.html |título=The Unreasonable Effectiveness of Mathematics in the Natural Sciences |periódico=Communications on Pure and Applied Mathematics |número=1 |ultimo=Wigner |primeiro=Eugene |autorlink=Eugene Wigner |ano=1960 |paginas=1–14 |bibcode=1960CPAM...13....1W |doi=10.1002/cpa.3160130102 |arquivourl=https://web.archive.org/web/20110228152633/http://www.dartmouth.edu/~matc/MathDrama/reading/Wigner.html |arquivodata=28 de fevereiro de 2011 |volume=13}}</ref> |
|||
Há muito tempo, buscam-se um consenso quanto à [[definição]] do que é a matemática. No entanto, nas últimas décadas do século XX, tomou forma uma definição que tem ampla aceitação entre os [[matemático]]s: "a matemática é a ciência das regularidades" ([[padrões]]). Segundo esta definição, o trabalho do matemático consiste em examinar padrões abstratos, tanto reais como imaginários, visuais ou mentais. Ou seja, os matemáticos procuram regularidades nos [[número]]s, no espaço, na ciência e na imaginação e formulam [[teorias]] com as quais tentam explicar as relações observadas. Uma outra definição seria que a matemática é a investigação de estruturas abstratas definidas [[axioma]]ticamente, usando a [[lógica formal]] como [[estrutura]] comum. As estruturas específicas geralmente têm sua origem nas [[Ciência natural|ciências naturais]], mais comumente na [[física]], mas os matemáticos também definem e investigam estruturas por razões puramente internas à matemática ([[matemática pura]]), por exemplo, ao perceberem que as estruturas fornecem uma generalização unificante de vários subcampos ou uma ferramenta útil em cálculos comuns.<ref name=":0" /><ref name=":1">{{citar livro|título=(Segunda Série, Coleção Integrada, Livro 1) Geometria, Capítulo 1: Geometria de posição|editora=SAS - Sistema Ari de Sá|ano=2017|local=Fortaleza, Ceará|acessodata=26 de março de 2017}}</ref> |
|||
Historicamente, o conceito de [[Prova matemática|prova]] e o [[Rigor|rigor matemático]] associado apareceram pela primeira vez na [[Matemática da Grécia Antiga|matemática grega]], mais notavelmente na obra ''[[Os Elementos]]'' de [[Euclides]].<ref>{{Citar web|ultimo=Wise|primeiro=David|url=http://jwilson.coe.uga.edu/EMT668/EMAT6680.F99/Wise/essay7/essay7.htm|titulo=Eudoxus' Influence on Euclid's Elements with a close look at The Method of Exhaustion|acessodata=18 de janeiro de 2024|website=[[Universidade da Geórgia]]|arquivourl=https://web.archive.org/web/20190601004355/http://jwilson.coe.uga.edu/emt668/EMAT6680.F99/Wise/essay7/essay7.htm|arquivodata=1 de junho de 2019|urlmorta=live}}</ref> Desde o seu início, a matemática foi dividida principalmente em [[geometria]] e [[aritmética]] (a manipulação de [[Número natural|números naturais]] e [[Fração|frações]]), até os séculos XVI e XVII, quando a [[álgebra]]{{Nre|Aqui, ''álgebra'' é tomada em seu sentido moderno, que é, grosso modo, a arte de manipular [[Fórmula (lógica)|fórmulas]].}} e o [[cálculo infinitesimal]] foram introduzidos como novos campos. Desde então, a interação entre inovações matemáticas e [[Cronologia das descobertas científicas|descobertas científicas]] levou a um aumento correlacionado no desenvolvimento de ambas.<ref>{{Citar periódico |título=The Skeleton in the Closet: Should Historians of Science Care about the History of Mathematics? |data=setembro de 2011 |periódico=Isis |número=3 |ultimo=Alexander |primeiro=Amir |autorlink=Amir Alexander |paginas=475–480 |doi=10.1086/661620 |issn=0021-1753 |mr=2884913 |pmid=22073771 |volume=102}}</ref> No final do século XIX, a [[Fundamentos da matemática|crise fundamental da matemática]] levou à sistematização do [[Sistema axiomático|método axiomático]],<ref name="Kleiner_1991">{{Citar periódico |título=Rigor and Proof in Mathematics: A Historical Perspective |data=dezembro de 1991 |periódico=Mathematics Magazine |publicado=Taylor & Francis, Ltd. |número=5 |ultimo=Kleiner |primeiro=Israel |paginas=291–314 |doi=10.1080/0025570X.1991.11977625 |issn=0025-570X |jstor=2690647 |lccn=47003192 |mr=1141557 |oclc=1756877 |volume=64}}</ref> que anunciou um aumento dramático no número de áreas matemáticas e seus campos de aplicação. |
|||
A matemática é usada como uma ferramenta essencial em muitas áreas do conhecimento, tais como: [[engenharia]], [[medicina]], [[física]], [[química]], [[biologia]] e as [[ciências sociais]]. Em um ponto, a [[matemática aplicada]], ramo da matemática que se dedica a aplicabilidade da matemática em outras áreas do conhecimento, às vezes leva ao desenvolvimento de um novo ramo, como aconteceu com a [[estatística]] ou a [[teoria dos jogos]]. Em outro ponto, o estudo da [[matemática pura]], ou seja, o estudo da matemática pela matemática, sem a preocupação de uma aplicabilidade, muitas vezes mostrou-se útil anos ou séculos depois. Foi como aconteceu com os estudos das [[cônica]]s e da [[teoria dos números]] que, explorada pelos gregos, foram úteis respectivamente em descobertas sobre [[astronomia]] feitas por [[Kepler]] no século XVII, ou para o desenvolvimento de segurança ([[criptografia]]) em computadores nos dias de hoje.<ref name=":1" /> |
|||
== |
== Etimologia == |
||
A palavra ''matemática'' vem do [[Língua grega antiga|grego antigo]] ''máthēma'' e significa "aquilo que se aprende",<ref name="EOD_n">{{Citar enciclopédia|ultimo=Harper|primeiro=Douglas|url=https://www.etymonline.com/word/mathematic|titulo=Mathematic (n.)|data=28 de março de 2019|acessodata=25 de janeiro de 2024|arquivourl=https://web.archive.org/web/20130307093926/http://etymonline.com/index.php?term=mathematic&allowed_in_frame=0|arquivodata=7 de março de 2013|urlmorta=live}}</ref> "aquilo que se conhece", assim como "estudo" e "ciência". A palavra passou a ter o significado mais restrito e técnico de "estudo matemático" mesmo no [[Antiguidade Clássica|período clássico]].{{Nre|Este significado pode ser encontrado na obra ''República'' de Platão, Livro 6, Seção 510c.<ref>{{cite book|author=Plato |url=https://www.perseus.tufts.edu/hopper/text?doc=Plat.+Rep.+6.510c&fromdoc=Perseus%3Atext%3A1999.01.0168 |title=Republic, Book 6, Section 510c |url-status=live |archive-url=https://web.archive.org/web/20210224152747/http://www.perseus.tufts.edu/hopper/text?doc=Plat.+Rep.+6.510c&fromdoc=Perseus%3Atext%3A1999.01.0168 |archive-date=24 de fevereiro de 2021 |access-date=2 de fevereiro de 2024}}</ref> No entanto, Platão não usou uma palavra “matemática”; Aristóteles fez isto, comentando sobre isso.<ref>{{cite dictionary|last1=Liddell |first1=Henry George |author1-link=Henry Liddell |last2=Scott |first2=Robert |year=1940 |section=μαθηματική |title=A Greek–English Lexicon |publisher=[[Clarendon Press]] |access-date=2 de fevereiro de 2024}}</ref><ref>{{cite web |last=Harper |first=Douglas |date=20 de abril de 2022 |website=[[Online Etymology Dictionary]] |title=Mathematics (n.) |url=https://www.etymonline.com/word/mathematics |access-date=2 de fevereiro de 2024}}</ref>}} Seu [[adjetivo]] é ''mathēmatikós'' ({{Lang|grc|μαθηματικός}}), que significa "relacionado à aprendizagem" ou "estudioso", que também passou a significar "matemático".<ref>{{Citar enciclopédia|ultimo=Harper|primeiro=Douglas|url=https://www.etymonline.com/word/mathematical|titulo=Mathematical (adj.)|data=22 de dezembro de 2018|acessodata=25 de janeiro de 2024|arquivourl=https://web.archive.org/web/20221126170916/https://www.etymonline.com/word/mathematical|arquivodata=26 de novembro de 2022|urlmorta=live}}</ref> Em particular, ''mathēmatikḗ tékhnē'' ({{Lang|grc|μαθηματικὴ τέχνη}}; {{Lang-la|ars mathematica}}) significava "a arte matemática".<ref name="EOD_n" /> |
|||
{{Artigo principal|História da matemática}} |
|||
Da mesma maneira, uma das duas principais [[escolas de pensamento]] do [[Escola pitagórica|pitagorismo]] era conhecida em grego antigo como ''mathēmatikoi'' (μαθηματικοί) {{Mdash}} que na época significava "alunos" ao invés do significado moderno dado ao termo "matemáticos". Os pitagóricos foram provavelmente os primeiros a restringir o uso da palavra apenas ao estudo da [[aritmética]] e da [[geometria]]. Na época de [[Aristóteles]] (384-322 a.C.) este significado foi totalmente estabelecido.<ref>{{Citar periódico |título=The Etymology of Mathematical Terms |data=1965 |periódico=[[Pi Mu Epsilon Journal]] |número=2 |ultimo=Perisho |primeiro=Margaret W. |paginas=62–66 |issn=0031-952X |jstor=24338341 |lccn=58015848 |oclc=1762376 |volume=4}}</ref> |
|||
Além de reconhecer quantidades de objetos, o homem [[pré-história|pré-histórico]] aprendeu a contar quantidades abstratas como o [[tempo]]: [[dia]]s, [[Estação do ano|estações]] e [[ano]]s. A aritmética elementar ([[adição]], [[subtração]], [[multiplicação]] e [[divisão]]) também foi conquistada naturalmente. Acredita-se que esse conhecimento é anterior à [[escrita]] e, por isso, não há registros históricos. |
|||
Em [[latim]] até cerca de 1700, o termo ''matemática'' tinha como significado mais comum "[[astrologia]]" (ou às vezes "[[astronomia]]"); isto mudou gradualmente para o significado atual entre 1500 e 1800. Esta mudança resultou em vários erros de tradução: Por exemplo, a advertência de [[Agostinho de Hipona|Santo Agostinho]] de que os cristãos deveriam tomar cuidado com os ''mathematici'', que significa "astrólogos", às vezes é mal traduzida como uma condenação dos matemáticos.<ref name="Boas">{{Citar livro|título=Lion Hunting and Other Mathematical Pursuits: A Collection of Mathematics, Verse, and Stories|ultimo=Boas|primeiro=Ralph P.|editora=[[Mathematical Association of America]]|ano=1995|editor-sobrenome=Alexanderson|capitulo=What Augustine Didn't Say About Mathematicians|isbn=978-0-88385-323-8|lccn=94078313|oclc=633018890|autorlink=Ralph P. Boas Jr.|editor-sobrenome2=Mugler|editor-nome2=Dale H.}}</ref> |
|||
O primeiro objeto conhecido que confirma a habilidade de cálculo é o [[Osso de Ishango]], uma [[fíbula]] de [[babuíno]] com riscos que indicam uma [[Contagem (matemática)|contagem]], que data por volta de 20 000 anos atrás.<ref>{{citar web|url=http://www.math.buffalo.edu/mad/Ancient-Africa/ishango.html|título=An Old Mathematical Object|publicado=The Mathematics Department of The State University of New York at Buffalo|lingua=inglês|acessodata=21 de dezembro de 2008}}</ref> |
|||
== Áreas da matemática == |
|||
Muitos sistemas de numeração existiram. O [[Papiro de Rhind]] é um [[documento]] que resistiu ao tempo e mostra os numerais ''escritos'' no [[Antigo Egito]]. |
|||
Antes do período do [[Renascimento]], a matemática era dividida em duas áreas principais: a [[aritmética]], a manipulação dos números, e a [[geometria]], o estudo das formas.<ref>{{Citar livro|título=The Development of Mathematics|ultimo=Bell|primeiro=E. T.|editora=Dover Publications|ano=1945|capitulo=General Prospectus|isbn=978-0-486-27239-9|lccn=45010599|oclc=523284|autorlink=Eric Temple Bell|edição=2nd}}</ref> Alguns tipos de [[pseudociência]], como a [[numerologia]] e a [[astrologia]], não eram então claramente distinguidas da matemática.<ref>{{Citar livro|título=Mathematics in History, Culture, Philosophy, and Science|ultimo=Tiwari|primeiro=Sarju|editora=Mittal Publications|ano=1992|capitulo=A Mirror of Civilization|isbn=978-81-7099-404-6|lccn=92909575|oclc=28115124|edição=1st|local-publicação=Nova Deli}}</ref> |
|||
Durante o período do [[Renascimento]], surgiram mais dois campos de estudo matemáticos. A [[Notação matemática|notação]] deu origem à [[álgebra]] que, a grosso modo, consiste no estudo e na manipulação de [[Fórmula (lógica)|fórmulas]]. O [[Cálculo infinitesimal|cálculo]], que consiste nos dois subcampos ''[[Cálculo diferencial|diferencial]]'' e ''[[integral]]'', é o estudo de [[Função contínua|funções contínuas]] que modelam as [[Sistema dinâmico não linear|relações tipicamente não lineares]] entre quantidades representadas por [[Variável (matemática)|variáveis]]. Esta divisão em quatro áreas principais {{Ndash}} aritmética, geometria, álgebra, cálculo<ref>{{Citar livro|título=Mathematics in Society and History|ultimo=Restivo|primeiro=Sal|editora=Kluwer Academic Publishers|ano=1992|editor-sobrenome=Bunge|editor-nome=Mario|editor-link=Mario Bunge|series=Episteme|volume=20|capitulo=Mathematics from the Ground Up|isbn=0-7923-1765-3|lccn=25709270|oclc=92013695}}</ref> {{Ndash}} perdurou até o final do século XIX. Áreas como [[mecânica celeste]] e [[mecânica dos sólidos]] eram então estudadas por matemáticos, mas agora são consideradas pertencentes à [[física]].<ref>{{Citar livro|título=Leonhard Euler and the Foundations of Celestial Mechanics|ultimo=Musielak|primeiro=Dora|editora=Springer International Publishing|ano=2022|series=History of Physics|doi=10.1007/978-3-031-12322-1|isbn=978-3-031-12321-4|issn=2730-7549|oclc=1332780664|autorlink=Dora Musielak}}</ref> O tema da [[combinatória]] foi estudado durante grande parte da história registrada, mas não se tornou um ramo separado da matemática até o século XVII.<ref>{{Citar periódico |título=The roots of combinatorics |data=Maio de 1979 |periódico=Historia Mathematica |número=2 |ultimo=Biggs |primeiro=N. L. |paginas=109–136 |doi=10.1016/0315-0860(79)90074-0 |issn=0315-0860 |lccn=75642280 |oclc=2240703 |volume=6 |doi-access=free}}</ref> |
|||
O desenvolvimento da matemática permeou as primeiras civilizações e tornou possível o desenvolvimento de aplicações concretas: o [[comércio]], o manejo de plantações, a [[medição]] de terra, astronomia, registro do tempo e, por vezes, a realização de rituais religiosos. |
|||
No final do século XIX, a [[Fundamentos da matemática|crise fundamental da matemática]] e a resultante sistematização do [[Sistema axiomático|método axiomático]] levaram a uma explosão de novas [[áreas da matemática]] nunca antes vista.<ref name="Warner_2013">{{Citar web|ultimo=Warner|primeiro=Evan|url=https://www.math.columbia.edu/~warner/notes/SplashTalk.pdf|titulo=Splash Talk: The Foundational Crisis of Mathematics|acessodata=3 de fevereiro de 2024|publicado=[[Universidade Columbia]]|arquivourl=https://web.archive.org/web/20230322165544/https://www.math.columbia.edu/~warner/notes/SplashTalk.pdf|arquivodata=22 de março de 2023|urlmorta=dead}}</ref><ref name="Kleiner_1991"/> A edição de 2020 da Classificação de Disciplinas de Matemática, por exemplo, contém nada menos que 63 áreas matemáticas consideradas de primeiro nível.<ref>{{Citar periódico |url=https://www.ams.org/journals/notices/202003/rnoti-p410.pdf |título=Mathematics Subject Classification 2020 |data=Março de 2020 |acessodata=3 de fevereiro de 2024 |periódico=Notices of the American Mathematical Society |número=3 |ultimo=Dunne |primeiro=Edward |ultimo2=Hulek |primeiro2=Klaus |paginas=410–411 |doi=10.1090/noti2052 |issn=0002-9920 |lccn=sf77000404 |oclc=1480366 |arquivourl=https://web.archive.org/web/20210803203928/https://www.ams.org/journals/notices/202003/rnoti-p410.pdf |arquivodata=3 de agosto de 2021 |volume=67 |doi-access=free}}</ref> Algumas delas correspondem à divisão mais antiga, como é o caso da [[teoria dos números]] e da geometria. Várias outras têm "geometria" em seus nomes ou são comumente consideradas parte da geometria. Álgebra e cálculo não aparecem como áreas de primeiro nível, mas são campos divididos em várias áreas. Outras áreas de primeiro nível surgiram durante o século XX ou não eram consideradas anteriormente como parte da matemática, como a [[Lógica matemática|lógica]] e os [[Fundamentos da matemática|fundamentos matemáticos]].<ref name="MSC">{{Citar web|url=https://zbmath.org/static/msc2020.pdf|titulo=MSC2020-Mathematics Subject Classification System|acessodata=3 de fevereiro de 2024|website=zbMath|publicado=Associate Editors of Mathematical Reviews and zbMATH|arquivourl=https://web.archive.org/web/20240102023805/https://zbmath.org/static/msc2020.pdf|arquivodata=2 de janeiro de 2024|urlmorta=live}}</ref> |
|||
A partir de 3000 a.C., quando Babilônios e Egípcios começaram a usar aritmética e geometria em construções, astronomia e alguns cálculos financeiros, a matemática começou a se tornar um pouco mais sofisticada.<ref>{{citar web|título=Babilônia|url=http://plato.if.usp.br/1-2003/fmt0405d/apostila/antig3/node3.html|publicado=IFUSP|acessodata=6 de Abril de 2016}}</ref> O estudo de estruturas matemáticas começou com a aritmética dos [[números naturais]], seguiu com a extração de raízes quadradas e cúbicas, resolução de algumas [[equação polinomial|equações polinomiais]] de segundo grau, [[trigonometria]], [[frações]], entre outros tópicos. |
|||
=== Teoria dos Números === |
|||
[[Imagem:Euclid Pisano OPA Florence.jpg|thumb|180px|Euclides: painel em mármore no ''[[Museo dell'Opera di Santa Maria del Fiore]]'']] |
|||
{{AP|Teoria dos números}} |
|||
Tais desenvolvimentos são creditados às civilizações acadiana, babilônica, egípcia, chinesa, ou ainda, àquelas [[Civilização do Vale do Indo|do vale do Indo]]. Por volta de 600 a.C., na [[civilização]] grega, a matemática, influenciada por trabalhos anteriores e pela [[filosofia]], tornou-se mais abstrata. Dois ramos se distinguiram: a [[aritmética]] e a [[geometria]]. Formalizaram-se as generalizações, por meio de definições axiomáticas dos objetos de estudo, e as demonstrações. A obra ''[[Os Elementos]], de Euclides,'' é um registro importante do conhecimento matemático na Grécia do século III a.C.. |
|||
[[Ficheiro:Spirale_Ulam_150.jpg|miniaturadaimagem| Esta é a [[espiral de Ulam]], que ilustra a distribuição dos [[Número primo|números primos]]. As linhas diagonais escuras na espiral sugerem a hipótese de [[Independência (estatística)|independência]] aproximada entre ser primo e ser um valor de um [[polinômio]] quadrático, uma conjectura agora conhecida como [[Espiral de Ulam|Conjectura F de Hardy e Littlewood]].]] |
|||
A [[teoria dos números]] teve início com as primeiras manipulações dos [[Número natural|números naturais]] <math>(\mathbb{N})</math> e posteriormente expandiu-se para [[Número inteiro|números inteiros]] <math>(\Z)</math> e [[Número racional|números racionais]] <math>(\Q)</math>. Ela já foi chamada de aritmética, mas atualmente este termo é usado principalmente para se referir aos [[Análise numérica|cálculos numéricos]].<ref>{{Citar livro|título=Fundamentals of Number Theory|ultimo=LeVeque|primeiro=William J.|editora=Addison-Wesley Publishing Company|ano=1977|páginas=1–30|capitulo=Introduction|isbn=0-201-04287-8|lccn=76055645|oclc=3519779}}</ref> A teoria dos números remonta à antiga [[Matemática babilônica|Babilônia]] e provavelmente à [[História da China|China Antiga]]. Dois proeminentes teóricos deste campo de estudo matemático foram os gregos [[Euclides]] e [[Diofanto de Alexandria]].<ref>{{Citar livro|título=The Queen of Mathematics: A Historically Motivated Guide to Number Theory|ultimo=Goldman|primeiro=Jay R.|editora=A K Peters|ano=1998|páginas=2–3|capitulo=The Founding Fathers|doi=10.1201/9781439864623|isbn=1-56881-006-7|lccn=94020017|oclc=30437959|local-publicação=Wellesley, MA}}</ref> O estudo moderno da teoria dos números na sua forma abstrata é amplamente atribuído a [[Pierre de Fermat]] e [[Leonhard Euler]], mas este campo se concretizou totalmente com as contribuições do francês [[Adrien-Marie Legendre]] e do alemão [[Carl Friedrich Gauss]].<ref>{{Citar livro|título=Number Theory: An Approach Through History From Hammurapi to Legendre|ultimo=Weil|primeiro=André|editora=Birkhäuser Boston|ano=1983|páginas=2–3|doi=10.1007/978-0-8176-4571-7|isbn=0-8176-3141-0|lccn=83011857|oclc=9576587|autorlink=André Weil}}</ref> |
|||
Muitos problemas numéricos têm soluções que requerem métodos sofisticados. Um exemplo proeminente é o [[Último Teorema de Fermat]], conjectura descrita no ano de 1637 por [[Pierre de Fermat]], mas que [[Resolução do último teorema de Fermat|foi provada]] apenas em 1994 por [[Andrew Wiles]], que usou ferramentas incluindo [[Esquema (matemática)|teoria de esquemas]] de [[geometria algébrica]], [[Teoria das categorias|teoria de categorias]] e [[álgebra homológica]].<ref>{{Citar periódico |título=From Fermat to Wiles: Fermat's Last Theorem Becomes a Theorem |data=março de 2000 |periódico=Elemente der Mathematik |número=1 |ultimo=Kleiner |primeiro=Israel |paginas=19–37 |doi=10.1007/PL00000079 |issn=0013-6018 |lccn=66083524 |oclc=1567783 |volume=55 |doi-access=free}}</ref> Outro exemplo é a [[Conjectura de Goldbach]], que afirma que todo número inteiro par maior que 2 é a soma de dois [[Número primo|números primos]]. Declarada em 1742 por [[Christian Goldbach]], permanece sem comprovação, apesar de esforços consideráveis.<ref>{{Citar livro|título=The Goldbach Conjecture|ultimo=Wang|primeiro=Yuan|editora=[[World Scientific]]|ano=2002|series=Series in Pure Mathematics|volume=4|páginas=1–18|doi=10.1142/5096|isbn=981-238-159-7|lccn=2003268597|oclc=51533750|edição=2nd}}</ref> |
|||
A civilização muçulmana permitiu que a herança grega fosse conservada e propiciou seu confronto com as descobertas chinesas e hindus, notadamente na questão da representação numérica.{{Carece de fontes|ciência=sim|data=Dezembro de 2008}} Os trabalhos matemáticos desenvolveram-se consideravelmente tanto na trigonometria, com a introdução das funções trigonométricas, quanto na aritmética. Desenvolveu-se ainda a [[combinatória|análise combinatória]], a [[análise numérica]] e a [[polinômio|álgebra de polinômios]]. |
|||
A teoria dos números abrange inúmeras subáreas, como [[teoria analítica dos números]], [[teoria algébrica dos números]], [[geometria dos números]] (orientada a métodos), [[Equação diofantina|equações diofantinas]] e [[teoria da transcendência]] (orientada a problemas).<ref name="MSC">{{Citar web|url=https://zbmath.org/static/msc2020.pdf|titulo=MSC2020-Mathematics Subject Classification System|acessodata=3 de fevereiro de 2024|website=zbMath|publicado=Associate Editors of Mathematical Reviews and zbMATH|arquivourl=https://web.archive.org/web/20240102023805/https://zbmath.org/static/msc2020.pdf|arquivodata=2 de janeiro de 2024|urlmorta=live}}</ref> |
|||
Na época do Renascentismo, uma parte dos textos árabes foi estudada e traduzida para o [[latim]]. A pesquisa matemática se concentrou então na [[Europa]]. O cálculo algébrico desenvolveu-se rapidamente com os trabalhos dos franceses [[François Viète]]<ref>{{citar periódico |url=https://fundacionorotava.org/media/web/publication_files/publication29__11.pdf |título=¿François Viète, Inventor Del Álgebra? |acessodata=8 de maio de 2023 |publicado=Fundacion Orotava |formato=PDF}}</ref> e [[René Descartes]]. Nessa época também foram criadas as tabelas de [[logaritmos]], que foram extremamente importantes para o avanço científico dos séculos XVI a XX, sendo substituídas apenas após a criação de computadores. A percepção de que os números reais não são suficientes para resolução de certas equações também data do século XVI. Já nessa época, começou o desenvolvimento dos chamados [[números complexos]], apenas com uma definição e quatro operações. Uma compreensão mais profunda dos números complexos só foi conquistada no século XVIII com [[Leonhard Euler|Euler]]. |
|||
=== Geometria === |
|||
No início do [[século XVII]], [[Isaac Newton]] e [[Gottfried Wilhelm Leibniz]] descobriram a noção de [[cálculo infinitesimal]] e introduziram a noção de ''fluxor'' (vocábulo abandonado posteriormente). Ao longo dos séculos XVIII e XIX, a matemática se desenvolveu fortemente com a introdução de novas estruturas abstratas, notadamente os [[Grupo (matemática)|grupos]] (graças aos trabalhos de [[Évariste Galois]]) sobre a resolubilidade de equações polinomiais, e os [[Anel (matemática)|anéis]], definidos nos trabalhos de [[Richard Dedekind]]. |
|||
{{AP|Geometria}} |
|||
[[Ficheiro:Triangles_(spherical_geometry).jpg|miniaturadaimagem|Na superfície de uma esfera, a [[geometria euclidiana]] só se aplica como aproximação local. Para escalas maiores a soma dos ângulos de um triângulo não é igual a 180°.]] |
|||
A [[geometria]] é um dos ramos mais antigos da matemática e começou com receitas empíricas sobre formas, como [[Reta|linhas]], [[Ângulo|ângulos]] e [[Circunferência|círculos]], que foram desenvolvidas principalmente para a [[Agrimensura|topografia]] e a [[arquitetura]], mas desde então floresceram em muitos outros subcampos.<ref name="Straume_2014">{{Citar arXiv|arxiv=1409.1140|classe=math.HO|nome=Eldar|sobrenome=Straume|titulo=A Survey of the Development of Geometry up to 1870|data=4 de setembro de 2014}}</ref> |
|||
Uma inovação fundamental foi a introdução, pelos antigos gregos, do conceito de [[Prova matemática|provas]], que exige que cada afirmação seja ''provada''. Por exemplo, não é suficiente verificar por [[medição]] que, digamos, dois comprimentos são iguais; sua igualdade deve ser provada através do raciocínio a partir de resultados previamente aceitos ([[Teorema|teoremas]]) e de algumas afirmações básicas que não estão sujeitas a prova porque são evidentes ([[Axioma|postulados]]) ou que fazem parte da definição do objeto de estudo ([[Axioma|axiomas]]). Este princípio, fundamental para toda a matemática, foi elaborado pela primeira vez para a geometria e foi sistematizado por [[Euclides]] por volta do ano 300 a.C. em sua obra ''[[Os Elementos]]''.<ref>{{Citar livro|url={{GBurl|id=8ZBsAAAAMAAJ}}|título=The Foundations of Geometry|ultimo=Hilbert|primeiro=David|editora=Open Court Publishing Company|ano=1902|doi=10.1126/science.16.399.307|lccn=02019303|oclc=996838|autorlink=David Hilbert|acessodata=6 de fevereiro de 2024}} {{Acesso gratuito}}</ref><ref>{{Citar livro|url={{GBurl|id=EJCSL9S6la0C|p=9}}|título=Geometry: Euclid and Beyond|ultimo=Hartshorne|primeiro=Robin|editora=Springer New York|ano=2000|páginas=9–13|capitulo=Euclid's Geometry|isbn=0-387-98650-2|lccn=99044789|oclc=42290188|autorlink=Robin Hartshorne|acessodata=7 de fevereiro de 2024}}</ref> |
|||
O rigor em matemática variou ao longo do tempo: os gregos antigos foram bastante rigorosos em suas argumentações; já no tempo da criação do Cálculo Diferencial e Integral, como as definições envolviam a noção de [[limite]] que, pelo conhecimento da época, só poderia ser tratada intuitivamente, o rigor foi menos intenso e muitos resultados eram estabelecidos com base na intuição. Isso levou a contradições e "falsos [[teoremas]]". Com isso, por volta do [[século XIX]], alguns matemáticos, tais como [[Bernard Bolzano|Bolzano]], [[Karl Weierstrass]] e [[Cauchy]] dedicaram-se a criar definições e demonstrações mais rigorosas. |
|||
A [[geometria euclidiana]] é o estudo das formas e seus arranjos [[Construções com régua e compasso|construídos]] a partir de retas, [[Plano (geometria)|planos]] e círculos no [[Plano (geometria)|plano]] e no [[espaço euclidiano]] tridimensional.{{Nre|Isso inclui [[Cónica|seções cônicas]]s, que são interseções de [[cilindro]]s circulares e planos.}}<ref name="Straume_2014">{{Citar arXiv|arxiv=1409.1140|classe=math.HO|nome=Eldar|sobrenome=Straume|titulo=A Survey of the Development of Geometry up to 1870|data=4 de setembro de 2014}}</ref> Foi desenvolvida sem mudança de métodos ou escopo até o século XVII, quando [[René Descartes]] introduziu o que hoje é chamado de [[Sistema de coordenadas cartesiano|coordenadas cartesianas]], o que constituiu uma grande [[mudança de paradigma]]: em vez de definir [[Número real|números reais]] como comprimentos de segmentos de reta (ver [[reta numérica]]), permitiu a representação de pontos usando suas ''coordenadas'', que são números. A álgebra (e mais tarde o cálculo) pode, portanto, ser usada para resolver problemas geométricos. A geometria foi dividida em dois novos subcampos: [[geometria sintética]], que utiliza métodos puramente geométricos, e [[geometria analítica]], que utiliza coordenadas sistemicamente.<ref>{{Citar livro|título=History of Analytic Geometry|ultimo=Boyer|primeiro=Carl B.|editora=[[Dover Publications]]|ano=2004|páginas=74–102|capitulo=Fermat and Descartes|isbn=0-486-43832-5|lccn=2004056235|oclc=56317813|autorlink=Carl B. Boyer}}</ref> A geometria analítica permite o estudo de [[Curva|curvas]] não relacionadas a círculos e linhas. Tais curvas podem ser definidas como o gráfico de funções, cujo estudo levou à [[geometria diferencial]]. Elas também podem ser definidas como [[Função implícita|equações implícitas]], muitas vezes [[Equação algébrica|equações polinomiais]] (que geraram a [[geometria algébrica]]). A geometria analítica também permite considerar espaços euclidianos superiores a três dimensões.<ref name="Straume_2014" /> |
|||
A matemática ainda continua a se desenvolver intensamente por todo o mundo nos dias de hoje. |
|||
A [[geometria analítica]] permite o estudo das [[Curva|curvas]] não relacionadas a círculos e linhas que podem ser definidas como o gráfico de funções, cujo estudo levou ao surgimento da área da [[geometria diferencial]]. Tais curvas também podem ser definidas como [[Função implícita|equações implícitas]], muitas vezes [[Equação algébrica|equações polinomiais]] (que geraram a [[geometria algébrica]]). A geometria analítica também permite considerar espaços euclidianos superiores a três dimensões.<ref name="Straume_2014">{{Citar arXiv|arxiv=1409.1140|classe=math.HO|nome=Eldar|sobrenome=Straume|titulo=A Survey of the Development of Geometry up to 1870|data=4 de setembro de 2014}}</ref> |
|||
=== No Brasil === |
|||
{{Artigo principal|História do ensino de matemática no Brasil}} |
|||
O ensino da matemática e, na verdade, de outras matérias, desde o [[descobrimento do Brasil]], era ministrado pelos [[jesuítas]] até a [[Expulsão dos jesuítas de Portugal|expulsão deles em 1759]]. Desta data até 1808, os ex-alunos dos jesuítas ficaram encarregados pelo ensino. De 1808 a 1834, a matéria era ministrada nas escolas do Exército e da Marinha e, a partir de 1873, também nas escolas de engenharia. Em 1874, é criada a [[Escola Politécnica da Universidade Federal do Rio de Janeiro|Escola Politécnica]] a partir da Escola Central, ex-Escola Militar. A [[Escola de Minas de Ouro Preto]] é criada em 1875 e a [[Escola Politécnica de São Paulo]] em 1893. Assim, o ensino de matemática passa também a ser oferecido em escolas não militares.<ref name="múltipla">Honig, Chain S. e Gomide, Elza F. Capítulo 2: Ciências matemáticas. Pp. 35-60. In: História das ciências no Brasil. Coordenação: Ferri, Mário Guimarães e Motoyama, Shozo. São Paulo: EPU: Ed. da [[Universidade de São Paulo]], 1979. 390p.</ref> |
|||
No século XIX, os matemáticos descobriram [[Geometria não euclidiana|geometrias não euclidianas]], ou seja, que não seguem o [[postulado das paralelas]]. Ao questionar a verdade deste postulado, esta descoberta foi interpretada como uma adesão ao [[Paradoxo de Russell]] ao revelar a [[Fundamentos da matemática|crise fundamental da matemática]]. Este aspecto da crise foi resolvido por meio da sistematização do método axiomático e pela noção de que a verdade dos axiomas escolhidos, na verdade, não é um [[problema matemático]].<ref>{{Citar periódico |url=https://philpapers.org/archive/STURTU.pdf |título=Reconstructing the Unity of Mathematics circa 1900 |acessodata=8 de fevereiro de 2024 |periódico=Perspectives on Science |número=3 |ultimo=Stump |primeiro=David J. |ano=1997 |pagina=383–417 |doi=10.1162/posc_a_00532 |issn=1063-6145 |lccn=94657506 |oclc=26085129 |volume=5}}</ref><ref name="Kleiner_1991"/> Por sua vez, o método axiomático permite o estudo de diversas geometrias obtidas quer pela alteração dos axiomas, quer pela consideração de propriedades que [[Invariante|não mudam]] sob transformações específicas do [[Espaço matemático|espaço]].<ref>{{Citar web|ultimo=O'Connor|primeiro=J. J.|ultimo2=Robertson|primeiro2=E. F.|titulo=Non-Euclidean geometry|data=Fevereiro de 1996|acessodata=8 de fevereiro de 2024|publicação=Escócia|publicado=[[Universidade de St. Andrews]]|url=https://web.archive.org/web/20221106142807/https://mathshistory.st-andrews.ac.uk/HistTopics/Non-Euclidean_geometry/|url=https://mathshistory.st-andrews.ac.uk/HistTopics/Non-Euclidean_geometry/|arquivodata=6 de novembro de 2022|urlmorta=live}}</ref> |
|||
== Áreas e metodologia == |
|||
As regras que governam as operações [[aritmética]]s são as da [[álgebra elementar]], e as propriedades mais profundas dos números inteiros são estudadas na [[teoria dos números]]. A investigação de métodos para resolver equações algébricas leva ao campo da [[álgebra abstrata]], que, entre outras coisas, estuda [[Teoria dos anéis|anéis]] e [[Corpo (matemática)|corpos]] — estruturas que generalizam as propriedades possuídas pelos [[número]]s. O conceito de [[Vetor (matemática)|vetor]], importante para a física, é generalizado no [[espaço vetorial]] e estudado na [[álgebra linear]], pertencendo aos dois ramos da estrutura e do espaço. |
|||
As subáreas atuais da geometria incluem:<ref name="MSC">{{Citar web|url=https://zbmath.org/static/msc2020.pdf|titulo=MSC2020-Mathematics Subject Classification System|acessodata=3 de fevereiro de 2024|website=zbMath|publicado=Associate Editors of Mathematical Reviews and zbMATH|arquivourl=https://web.archive.org/web/20240102023805/https://zbmath.org/static/msc2020.pdf|arquivodata=2 de janeiro de 2024|urlmorta=live}}</ref> |
|||
[[Imagem:Woman teaching geometry.jpg|thumb|esquerda|180px|O ensino da geometria]] |
|||
* [[Geometria projetiva]], introduzida no século XVI por [[Girard Desargues]], estende a geometria euclidiana adicionando [[Ponto impróprio|pontos impróprios]] nos quais [[Paralelismo|linhas paralelas]] se cruzam. Isto simplifica muitos aspectos da geometria clássica, unificando os tratamentos para linhas paralelas e que se cruzam. |
|||
O estudo do espaço se originou com a [[geometria]], primeiro com a [[geometria euclidiana]] e a [[trigonometria]]; mais tarde, foram generalizadas nas geometrias não-euclidianas, as quais cumprem um papel central na formulação da [[teoria da relatividade]]. A [[teoria de Galois]] permitiu resolverem-se várias questões sobre construções geométricas com régua e compasso. A [[geometria diferencial]] e a [[geometria algébrica]] generalizam a geometria em diferentes direções: a geometria diferencial enfatiza o conceito de [[sistemas de coordenadas]], equilíbrio e direção, enquanto na geometria algébrica os objetos geométricos são descritos como conjuntos de solução de [[equação polinomial|equações polinomiais]]. A [[teoria dos grupos]] investiga o conceito de [[simetria]] de forma abstrata e fornece uma ligação entre os estudos do espaço e da estrutura. A [[Topologia (matemática)|topologia]] conecta o estudo do espaço e o estudo das transformações, focando-se no conceito de continuidade. |
|||
* [[Geometria afim]], o estudo das propriedades relativas ao [[paralelismo]] e independentes do conceito de comprimento. |
|||
* [[Geometria diferencial]], o estudo de curvas, superfícies e suas generalizações, que são definidas por meio de [[Função diferenciável|funções diferenciáveis]]. |
|||
* [[Variedade (matemática)|Teoria múltipla]], o estudo de formas que não estão necessariamente incorporadas em um espaço maior. |
|||
* [[Geometria de Riemann|Geometria riemanniana]], o estudo das propriedades de distância em espaços curvos. |
|||
* [[Geometria algébrica]], o estudo de curvas, superfícies e suas generalizações, que são definidas por meio de [[Polinómio|polinômios]]. |
|||
* [[Topologia (matemática)|Topologia]], estudo das propriedades que se mantêm sob [[Homotopia|deformações contínuas]]. |
|||
** [[Topologia algébrica]], o uso em topologia de métodos algébricos, principalmente [[álgebra homológica]]. |
|||
* [[Geometria discreta]], o estudo de configurações finitas em geometria. |
|||
* [[Geometria convexa]], estudo de [[Conjunto convexo|conjuntos convexos]]. |
|||
* [[Geometria complexa]], a geometria obtida pela substituição de números reais por [[Número complexo|números complexos]]. |
|||
=== Álgebra === |
|||
Entender e descrever as alterações em quantidades mensuráveis é o tema comum das ciências naturais e o [[cálculo]] foi desenvolvido como a ferramenta mais útil para fazer isto. A descrição da variação de valor de uma grandeza é obtida por meio do conceito de [[função (matemática)|função]]. O campo das [[equação diferencial|equações diferenciais]] fornece métodos para resolver problemas que envolvem relações entre uma grandeza e suas variações. Os [[número real|números reais]] são usados para representar as quantidades contínuas e o estudo detalhado das suas propriedades e das propriedades de suas funções consiste na [[análise real]], a qual foi generalizada para [[análise complexa]], abrangendo os [[número complexo|números complexos]]. A [[análise funcional]] trata de funções definidas em espaços de dimensões tipicamente infinitas, constituindo a base para a formulação da [[mecânica quântica]], entre muitas outras coisas. |
|||
{{AP|Álgebra}} |
|||
[[Ficheiro:Quadratic_formula.svg|miniaturadaimagem| A [[fórmula quadrática]], que expressa concisamente as soluções de todas as [[Equação quadrática|equações quadráticas]]]] |
|||
[[Ficheiro:Rubik's_cube.svg|miniaturadaimagem| O grupo [[Cubo de Rubik]] é uma aplicação concreta da [[teoria dos grupos]]<ref>{{Citar livro|título=Adventures in Group Theory: Rubik's Cube, Merlin's Machine, and Other Mathematical Toys|ultimo=Joyner|primeiro=David|editora=[[Johns Hopkins University]]|ano=2008|páginas=219–232|capitulo=The (legal) Rubik's Cube group|isbn=978-0-8018-9012-3|lccn=2008011322|oclc=213765703|edição=2nd}}</ref>]] |
|||
A [[álgebra]] é a arte de manipular [[Equação|equações]] e fórmulas. [[Diofanto]] (século III) e [[Alcuarismi]] (século IX) foram os dois principais precursores deste campo de estudo matemático.<ref>{{Citar periódico |título=Practicing algebra in late antiquity: The problem-solving of Diophantus of Alexandria |data=Maio de 2013 |periódico=Historia Mathematica |número=2 |ultimo=Christianidis |primeiro=Jean |ultimo2=Oaks |primeiro2=Jeffrey |paginas=127–163 |doi=10.1016/j.hm.2012.09.001 |issn=0315-0860 |lccn=75642280 |oclc=2240703 |volume=40 |doi-access=free}}</ref>{{Sfn|Kleiner|2007|loc="History of Classical Algebra" pp. 3–5}} O grego Diofanto resolveu algumas equações envolvendo números naturais desconhecidos ao deduzir novas relações até obter a solução. O persa Alcuarismi, por sua vez, introduziu métodos sistemáticos para transformar equações, como mover um termo de um lado de uma equação para o outro lado. O termo "''álgebra''" é derivado da palavra [[Língua árabe|árabe]] ''al-jabr'' que significa 'a reunião de partes quebradas' que ele usou para nomear um desses métodos no título de [[Livro da Restauração e do Balanceamento|seu tratado principal]].<ref>{{Citar web|ultimo=Lim|primeiro=Lisa|url=https://www.scmp.com/magazines/post-magazine/short-reads/article/2178856/where-x-we-use-algebra-came-and-x-xmas|titulo=Where the x we use in algebra came from, and the X in Xmas|data=21 de dezembro de 2018|acessodata=8 de fevereiro de 2024|website=[[South China Morning Post]]|arquivourl=https://web.archive.org/web/20181222003908/https://www.scmp.com/magazines/post-magazine/short-reads/article/2178856/where-x-we-use-algebra-came-and-x-xmas|arquivodata=22 de dezembro de 2018|urlmorta=live}}</ref> |
|||
A álgebra tornou-se uma área independente apenas com [[François Viète]] (1540-1603), que introduziu o uso de variáveis para representar números desconhecidos ou não especificados.<ref>{{Citar periódico |url=https://researchoutreach.org/wp-content/uploads/2019/02/Jeffrey-Oaks.pdf |título=François Viète's revolution in algebra |acessodata=8 de fevereiro de 2024 |periódico=Archive for History of Exact Sciences |número=3 |ultimo=Oaks |primeiro=Jeffery A. |ano=2018 |paginas=245–302 |doi=10.1007/s00407-018-0208-0 |issn=0003-9519 |lccn=63024699 |oclc=1482042 |arquivourl=https://web.archive.org/web/20221108162134/https://researchoutreach.org/wp-content/uploads/2019/02/Jeffrey-Oaks.pdf |arquivodata=8 de novembro de 2022 |volume=72}}</ref> |
|||
Para esclarecer e investigar os [[fundamentos da matemática]], foram desenvolvidos os campos da [[teoria dos conjuntos]], [[lógica matemática]] e [[teoria dos modelos]]. |
|||
Até o século XIX, a álgebra consistia principalmente no estudo de [[Equação linear|equações lineares]] (atualmente [[álgebra linear]]) e de [[equações polinomiais]] em uma única [[Equação|incógnita]], que eram chamadas de ''[[equações algébricas]]'' (termo ainda em uso, embora possa ser ambíguo). Durante o século XIX, os matemáticos começaram a usar variáveis para representar outras coisas além dos números (como [[Matriz (matemática)|matrizes]], [[Aritmética modular|inteiros modulares]] e [[Transformação geométrica|transformações geométricas]]), nas quais generalizações de operações aritméticas são frequentemente válidas.{{Sfn|Kleiner|2007|loc="History of Linear Algebra" pp. 79–101}} O conceito de [[estrutura algébrica]] aborda isto, consistindo em um [[conjunto]] cujos elementos não são especificados, em operações que atuam sobre os elementos do conjunto e em regras que essas operações devem seguir. O escopo da álgebra cresceu assim para incluir o estudo de estruturas algébricas. Este objeto da álgebra foi denominado ''álgebra moderna'' ou [[álgebra abstrata]], conforme estabelecido pela influência e trabalhos da matemática alemã [[Emmy Noether]].<ref>{{Citar livro|url={{GBurl|id=WdGbeyehoCoC|p=247}}|título=Modern Algebra and the Rise of Mathematical Structures|ultimo=Corry|primeiro=Leo|editora=Birkhäuser Basel|ano=2004|páginas=247–252|capitulo=Emmy Noether: Ideals and Structures|isbn=3-7643-7002-5|lccn=2004556211|oclc=51234417|autorlink=Leo Corry|acessodata=8 de fevereiro de 2024|edição=2ª revisada|local-publicação=Alemanha}}</ref> |
|||
Quando os [[computador]]es foram concebidos, várias questões teóricas levaram à elaboração das teorias da [[teoria da computabilidade|computabilidade]], [[teoria da complexidade computacional|complexidade computacional]], [[teoria da informação|informação]] e [[teoria da informação algorítmica|informação algorítmica]], as quais são investigadas na [[ciência da computação]]. |
|||
[[Imagem:Frans Hals - Portret van René Descartes.jpg|thumb|180px|[[René Descartes]]]] |
|||
Alguns tipos de estruturas algébricas têm propriedades úteis e muitas vezes fundamentais em muitas áreas da matemática. Seu estudo tornou-se parte autônoma da álgebra e inclui vários campos de estudos:<ref name="MSC">{{Citar web|url=https://zbmath.org/static/msc2020.pdf|titulo=MSC2020-Mathematics Subject Classification System|acessodata=3 de fevereiro de 2024|website=zbMath|publicado=Associate Editors of Mathematical Reviews and zbMATH|arquivourl=https://web.archive.org/web/20240102023805/https://zbmath.org/static/msc2020.pdf|arquivodata=2 de janeiro de 2024|urlmorta=live}}</ref> |
|||
Os computadores também contribuíram para o desenvolvimento da [[teoria do caos]], que trata do fato de que muitos sistemas dinâmicos não-lineares possuem um comportamento que, na prática, é imprevisível. A teoria do caos tem relações estreitas com a [[geometria dos fractais]], como o [[conjunto de Mandelbrot]] e de Mary, descoberto por Lorenz, conhecido pelo atrator que leva seu nome. |
|||
* [[teoria dos grupos]]; |
|||
Um importante campo na [[matemática aplicada]] é a [[estatística]], que permite a descrição, análise e previsão de fenômenos aleatórios e é usada em todas as ciências. A [[análise numérica]] investiga os métodos para resolver numericamente e de forma eficiente vários problemas usando computadores e levando em conta os erros de arredondamento. A matemática discreta é o nome comum para estes campos da matemática úteis na ciência computacional. |
|||
* [[Corpo (matemática)|teoria de campo]]; |
|||
* [[Espaço vetorial|espaços vetoriais]], cujo estudo é essencialmente igual ao da [[álgebra linear]]; |
|||
* [[teoria dos anéis]]; |
|||
* [[Álgebra comutativa|a álgebra comutativa]], que é o estudo dos [[Anel comutativo|anéis comutativos]], inclui o estudo dos [[Polinómio|polinômios]] e é uma parte fundamental da [[geometria algébrica]]; |
|||
* [[álgebra homológica]]; |
|||
* [[Álgebra de Lie]] e teoria dos [[Grupo de Lie|Grupos de Lie]]; |
|||
* [[Álgebra booliana]], que é amplamente utilizada para o estudo da estrutura lógica de [[Computador|computadores]]. |
|||
O estudo de tipos de estruturas algébricas como [[Objeto matemático|objetos matemáticos]] é o propósito da [[álgebra universal]] e da [[teoria das categorias]].<ref>{{Citar livro|url={{GBurl|id=ZoRN9T1GUVwC|p=3}}|título=Perspectives on Universal Logic|ultimo=Riche|primeiro=Jacques|editora=Polimetrica International Scientific Publisher|ano=2007|editor-sobrenome=Beziau|páginas=3–39|capitulo=From Universal Algebra to Universal Logic|isbn=978-88-7699-077-9|oclc=647049731|acessodata=8 de fevereiro de 2024|editor-sobrenome2=Costa-Leite|local-publicação=Milano, Italy}}</ref> Esta última se aplica a todas as estruturas matemáticas (não apenas às algébricas). Na sua origem foi introduzida juntamente com a [[álgebra homológica]] por permitir o estudo algébrico de objetos não algébricos como [[Espaço topológico|espaços topológicos]]; esta área específica de aplicação é chamada de [[topologia algébrica]].<ref>{{Citar livro|url={{GBurl|id=41bHxtHxjUAC|pg=PR20}}|título=Tool and Object: A History and Philosophy of Category Theory|ultimo=Krömer|primeiro=Ralph|editora=Springer Science & Business Media|ano=2007|series=Science Networks - Historical Studies|volume=32|páginas=xxi–xxv, 1–91|isbn=978-3-7643-7523-2|lccn=2007920230|oclc=85242858|acessodata=8 de fevereiro de 2024|local-publicação=Alemanha}}</ref> |
|||
Por fim, uma [[teoria]] importante desenvolvida pelo ganhador do [[Prémio Nobel]], [[John Forbes Nash|John Nash]], é a [[teoria dos jogos]], que possui atualmente aplicações nos mais diversos campos, como no estudo de disputas comerciais, pois uma de suas principais premissas é a de que todos os participantes querem obter o maior lucro possível. Entretanto, premissas deste tipo levantam restrições para a aplicação desta teoria em outras áreas, como a biologia, por exemplo. |
|||
== |
=== Cálculo e análise === |
||
{{ |
{{AP|Cálculo infinitesimal|Análise matemática}} |
||
[[Ficheiro:Cauchy_sequence_illustration.svg|miniaturadaimagem|Uma [[Sucessão de Cauchy|Sequência de Cauchy]] consiste em elementos tais que todos os termos subsequentes de um termo tornam-se arbitrariamente próximos uns dos outros à medida que a sequência avança (da esquerda para a direita).]] |
|||
[[Imagem:Infinity symbol.svg|thumb|esquerda|180px|O símbolo do [[infinito]] '''∞''' em várias formas]] |
|||
O [[cálculo]], anteriormente chamado de cálculo infinitesimal, foi introduzido de forma independente e simultânea por dois matemáticos do século XVII, [[Isaac Newton|Newton]] e [[Gottfried Wilhelm Leibniz|Leibniz]].<ref>{{Citar livro|título=The Oxford Handbook of Newton|ultimo=Guicciardini|primeiro=Niccolo|editora=[[Oxford University Press]]|ano=2017|editor-sobrenome=Schliesser|series=Oxford Handbooks|capitulo=The Newton–Leibniz Calculus Controversy, 1708–1730|doi=10.1093/oxfordhb/9780199930418.013.9|isbn=978-0-19-993041-8|oclc=975829354|autorlink=Niccolò Guicciardini|acessodata=9 de fevereiro de 2024|editor-sobrenome2=Smeenk|arquivourl=https://web.archive.org/web/20221109163253/https://core.ac.uk/download/pdf/187993169.pdf|url=https://core.ac.uk/download/pdf/187993169.pdf|arquivodata=9 de novembro de 2022}}</ref> É fundamentalmente o estudo da relação de variáveis que dependem umas das outras. O cálculo foi expandido no século XVIII por [[Leonhard Euler|Euler]] com a introdução do conceito de [[Função (matemática)|função]] e muitos outros resultados.<ref>{{Citar web|ultimo=O'Connor|primeiro=J. J.|ultimo2=Robertson|primeiro2=E. F.|titulo=Leonhard Euler|data=Setembro de 1998|acessodata=9 de fevereiro de 2024|editor=MacTutor|publicação=Escócia|publicado=[[Universidade de St. Andrews]]|arquivourl=https://web.archive.org/web/20221109164921/https://mathshistory.st-andrews.ac.uk/Biographies/Euler/|url=https://mathshistory.st-andrews.ac.uk/Biographies/Euler/|arquivodata=9 de novembro de 2022|urlmorta=live}}</ref> |
|||
A maior parte da notação matemática em uso atualmente não havia sido inventada até o século XVI.<ref>{{citar web|url=http://jeff560.tripod.com/mathsym.html|titulo=Earliest Uses of Various Mathematical Symbols}}</ref> Antes disso, os matemáticos escreviam tudo em palavras, um processo trabalhoso que limitava as descobertas matemáticas. No século XVIII, [[Leonhard Euler|Euler]] foi responsável por muitas das notações em uso atualmente. A notação moderna deixou a matemática muito mais fácil para os profissionais, mas os iniciantes normalmente acham isso desencorajador. Isso é extremamente compreensivo: alguns poucos símbolos contêm uma grande quantidade de [[informação]]. Assim como a [[notação musical]], a notação matemática moderna tem uma sintaxe restrita e informações que seriam difíceis de escrever de outro modo. |
|||
Atualmente, “cálculo” refere-se principalmente à parte elementar desta teoria, e “análise” é comumente usada para partes avançadas. A análise é subdividida em [[análise real]], onde as variáveis representam [[Número real|números reais]], e [[análise complexa]], onde as variáveis representam [[Número complexo|números complexos]]. Ela inclui muitas subáreas compartilhadas por outras áreas da matemática como:<ref name="MSC">{{Citar web|url=https://zbmath.org/static/msc2020.pdf|titulo=MSC2020-Mathematics Subject Classification System|acessodata=3 de fevereiro de 2024|website=zbMath|publicado=Associate Editors of Mathematical Reviews and zbMATH|arquivourl=https://web.archive.org/web/20240102023805/https://zbmath.org/static/msc2020.pdf|arquivodata=2 de janeiro de 2024|urlmorta=live}}</ref> |
|||
A língua matemática pode também ser difícil para os iniciantes. Palavras como ''"e"'' e "''ou"'' têm significados muito mais precisos do que a fala do dia-a-dia. Além disso, palavras como ''[[conjunto aberto|aberto]]'' e ''[[Campo (matemática)|campo]]'' têm recebido um significado matemático específico. O jargão matemático inclui termos técnicos como ''[[homeomorfismo]]'' e ''[[integral]]''. Mas há uma razão para a notação especial e o jargão técnico: matemática requer mais precisão do que a fala do dia-a-dia. Matemáticos se referem a essa precisão da [[linguagem]] e lógica como ''"rigor"''. |
|||
* [[Cálculo com múltiplas variáveis|Cálculo multivariável]]; |
|||
== Áreas da matemática == |
|||
* [[Análise funcional]], onde variáveis representam funções variáveis; |
|||
[[Imagem:Abacus 6.png|direita|thumb|O [[ábaco]] é uma ferramenta de cálculo simples utilizada desde os tempos antigos]] |
|||
* [[Integral|Integração]], [[Medida (matemática)|teoria da medida]] e [[teoria do potencial]], todas fortemente relacionadas com a [[teoria das probabilidades]] num [[Número real|continuum]]; |
|||
A matemática pode, em linhas gerais, ser subdividida nos estudos de quantidade, estrutura, espaço e mudança (i.e. [[aritmética]], [[álgebra]], [[geometria]], e [[análise matemática|análise]]). Além desses principais assuntos, também há subdivisões dedicadas a explorar as ligações do cerne da matemática a outros campos: à [[lógica matemática|lógica]], à [[teoria de conjuntos]] ([[fundações da matemática|fundações]]), à matemática empírica das várias ciências ([[matemática aplicada]]), e, mais recentemente, ao estudo rigoroso da [[incerteza]]. Enquanto algumas áreas da matemática possam parecer disjuntas, o [[programa Langlands]] tem encontrado conexões entre áreas como [[grupos de Galois]], [[superfície de Riemann]] e [[teoria dos números]]. |
|||
* [[Equação diferencial ordinária|Equações diferenciais ordinárias]]; |
|||
* [[Equação diferencial parcial|Equações diferenciais parciais]]; |
|||
* [[Análise numérica]], dedicada principalmente ao cálculo em computadores de soluções de equações diferenciais ordinárias e parciais que surgem em muitas aplicações. |
|||
=== |
=== Matemática discreta === |
||
{{AP|Matemática discreta}} |
|||
Para clarificar as [[fundações da matemática]], desenvolveram-se os campos como a [[matemática lógica]] e a [[teoria dos conjuntos]]. A lógica matemática inclui o estudo matemático da [[lógica]] e as aplicações de lógica formal em outras áreas da matemática; a teoria de conjuntos é o ramo da matemática que estuda [[conjunto (matemática)|conjuntos]] ou coleções de objetos. A [[teoria das categorias]], que lida de uma maneira abstrata com as [[Estrutura matemática|estruturas matemáticas]] e as relações entre elas, ainda está em desenvolvimento. A expressão "crise nas fundações" descreve a busca por uma fundação rigorosa para a matemática ocorrida, aproximadamente, de 1900 a 1930.<ref>Luke Howard Hodgkin & Luke Hodgkin, ''A History of Mathematics'', Oxford University Press, 2005.</ref> Algumas discordâncias sobre as fundações da matemática persistem atualmente. A crise de fundações foi estimulada por várias controvérsias à época, incluindo a [[Teorema de Cantor|controvérsia sobre a teoria de conjuntos de Cantor]] e a [[controvérsia de Brouwer–Hilbert]]. |
|||
[[Ficheiro:Markovkate_01.svg|direita|miniaturadaimagem| Um diagrama representando uma [[Cadeias de Markov|cadeia de Markov]] de dois estados. Os estados são representados por 'A' e 'E'. Os números são a probabilidade de inverter o estado.]] |
|||
A [[matemática discreta]], em termos gerais, é o estudo de objetos matemáticos individuais e [[Conjunto contável|contáveis]].<ref>{{Citar periódico |url=https://scholarship.claremont.edu/cgi/viewcontent.cgi?article=1334&context=jhm |título=Discrete and Continuous: A Fundamental Dichotomy in Mathematics |data=Julho de 2017 |acessodata=9 de fevereiro de 2024 |periódico=Journal of Humanistic Mathematics |número=2 |ultimo=Franklin |primeiro=James |autorlink=James Franklin (philosopher) |paginas=355–378 |doi=10.5642/jhummath.201702.18 |issn=2159-8118 |lccn=2011202231 |oclc=700943261 |volume=7 |doi-access=free}}</ref> Como os objetos de estudo aqui são discretos, os métodos de cálculo e análise matemática não se aplicam diretamente.{{Nre|No entanto, alguns métodos avançados de análise são por vezes utilizados; por exemplo, métodos de [[análise complexa]] aplicados à [[função geradora]].}} [[Algoritmo|Algoritmos]] {{Mdash}} especialmente sua [[Implementação de software|implementação]] e [[complexidade computacional]] {{Mdash}} desempenham um papel importante na matemática discreta.<ref>{{Citar livro|título=Discrete Mathematics in the Schools|ultimo=Maurer|primeiro=Stephen B.|editora=[[American Mathematical Society]]|ano=1997|editor-sobrenome=Rosenstein|series=DIMACS: Series in Discrete Mathematics and Theoretical Computer Science|volume=36|páginas=121–124|capitulo=What is Discrete Mathematics? The Many Answers|doi=10.1090/dimacs/036/13|isbn=0-8218-0448-0|issn=1052-1798|lccn=97023277|oclc=37141146|acessodata=9 de fevereiro de 2024|editor-sobrenome2=Franzblau|editor-sobrenome3=Roberts|editor-link3=Fred S. Roberts}}</ref> |
|||
O [[teorema das quatro cores]] e a [[conjectura de Kepler]] foram dois grandes problemas da matemática discreta resolvidos na segunda metade do século XX.<ref>{{Citar livro|título=Turing's Legacy|ultimo=Hales|primeiro=Thomas C.|editora=[[Cambridge University Press]]|ano=2014|editor-sobrenome=Downey|editor-nome=Rod|editor-link=Rod Downey|series=Lecture Notes in Logic|volume=42|páginas=260–261|capitulo=Turing's Legacy: Developments from Turing's Ideas in Logic|doi=10.1017/CBO9781107338579.001|isbn=978-1-107-04348-0|lccn=2014000240|oclc=867717052|autorlink=Thomas Callister Hales|acessodata=9 de fevereiro de 2024}}</ref> O [[P versus NP|problema P versus NP]], que permanece não solucionado até os dias atuais, também é importante para a matemática discreta, uma vez que sua solução impactaria potencialmente um grande número de problemas [[Análise de algoritmos|computacionalmente difíceis]].<ref>{{Citar conferência |ultimo=Sipser |primeiro=Michael |autorlink=Michael Sipser |titulo=The History and Status of the P versus NP Question |data=Julho de 1992 |paginas=603–618 |conferencia=STOC '92: Proceedings of the twenty-fourth annual ACM symposium on Theory of Computing |doi=10.1145/129712.129771}}</ref> |
|||
A lógica matemática está preocupada com um escopo [[axiom]]ático rigoroso, e com o estudo das implicações de tal escopo. Tal qual seja, a existência dos [[teoremas da incompletude de Gödel]] (informalmente) implicam que qualquer [[sistema formal]] efetivo que contém aritmética básica, se todos os teoremas nele contido puderem ser provados são verdadeiros, é necessariamente ''incompleto'' (significando que há teoremas verdadeiros que não podem ser provados ''nesse sistema formal''). Para qualquer coleção finita de axiomas da teoria dos números que seja tomada como fundação matemática, Gödel mostrou como construir um enunciado formal que é um fato verdadeiro na teoria dos números, mas que não decorrem dos axiomas. Logo, nenhum sistema formal é uma axiomatização completa da teoria dos números como um todo. A lógica moderna é dividida em [[teoria da computabilidade]], em [[teoria dos modelos]], e em [[teoria da prova]], e está intrinsecamente relacionada com a [[ciência da computação teórica]],{{Carece de fontes|ciência=sim|data=julho de 2021}} bem como com a [[teoria das categorias]]. No contexto da teoria da computabilidade, a impossibilidade de uma axiomatização completa da teoria dos números pode também ser formalmente demonstrado como uma [[consequência do teorema MRDP]]. |
|||
A matemática discreta inclui:<ref name="MSC">{{Citar web|url=https://zbmath.org/static/msc2020.pdf|titulo=MSC2020-Mathematics Subject Classification System|acessodata=3 de fevereiro de 2024|website=zbMath|publicado=Associate Editors of Mathematical Reviews and zbMATH|arquivourl=https://web.archive.org/web/20240102023805/https://zbmath.org/static/msc2020.pdf|arquivodata=2 de janeiro de 2024|urlmorta=live}}</ref> |
|||
A [[ciência da computação teórica]] inclui a [[teoria da computabilidade]], a [[teoria da complexidade computacional]], e a [[teoria da informação]]. A teoria da computabilidade examina as limitações de vários modelos teóricos do computador, incluindo o modelo mais bem conhecido: a [[máquina de Turing]]. A teoria da complexidade é o estudo da tratabilidade por computador; alguns problemas, apesar de serem teoricamente solúveis por computador, são tão caros em termos de tempo ou espaço que sua resolução é praticamente inatingível, até mesmo com o avanço rápido do hardware dos computadores. Um problema famoso é o problema "[[P versus NP|{{nowrap|'''P''' {{=}} '''NP'''?}}]]", um dos [[Problemas do Prêmio Millennium]].<ref>[https://web.archive.org/web/20070811193730/http://www.claymath.org/millennium/P_vs_NP/ Clay Mathematics Institute], P=NP, claymath.org</ref> Finalmente, a teoria da informação está interessada com a quantidade de dados que pode ser armazenada em um dado meio, e, portanto, lida com conceitos como [[compressão de dados|compressão]] e [[Entropia (teoria da informação)|entropia]]. |
|||
* [[Combinatória]], a arte de enumerar objetos matemáticos que satisfazem algumas restrições. Originalmente, estes objetos eram elementos ou [[Subconjunto|subconjuntos]] de um determinado [[conjunto]]; isto foi estendido a vários objetos, o que estabelece uma forte ligação entre a combinatória e outras partes da matemática discreta. Por exemplo, a [[geometria discreta]] inclui a contagem de configurações de [[Forma (figura)|formas geométricas]]; |
|||
{| style="border:1px solid #ddd; text-align:center; margin: auto;" cellspacing="20" |
|||
* [[Teoria dos grafos]] e [[Hipergrafo|hipergrafos]]; |
|||
| <math> p \Rightarrow q</math>|| [[Imagem:Venn A intersect B.svg|128px]] || [[Imagem:Commutative diagram for morphism.svg|96px]] || [[Imagem:DFAexample.svg|96px]] |
|||
* [[Teoria de códigos|Teoria da codificação]], incluindo [[Código de correção de erro|códigos de correção de erros]] e uma parte da [[criptografia]]; |
|||
|- |
|||
* Teoria [[matróide]]; |
|||
| [[Lógica matemática]] || [[Teoria dos conjuntos]] || [[Teoria das categorias]] || [[Teoria da computação]] |
|||
* [[Geometria discreta]]; |
|||
|} |
|||
* [[Distribuição de probabilidade|Distribuições de probabilidade discretas]]; |
|||
* [[Teoria dos jogos]] (embora os jogos contínuos também sejam estudados, os jogos mais comuns, como [[xadrez]] e [[pôquer]], são discretos); |
|||
* Otimização discreta, incluindo [[otimização combinatória]], [[programação inteira]], [[Programação por restrições|programação com restrições]]. |
|||
=== Lógica matemática e teoria dos conjuntos === |
|||
=== Matemática pura === |
|||
{{AP|Lógica matemática|Teoria dos conjuntos}} |
|||
==== Quantidades ==== |
|||
[[Ficheiro:Venn_A_intersect_B.svg|miniaturadaimagem|O [[diagrama de Venn]] é um método comumente usado para ilustrar as relações entre [[conjuntos]].]] |
|||
{{Artigo principal|Número}} |
|||
A disciplinas de [[lógica matemática]] e [[teoria dos conjuntos]] pertencem à matemática desde o final do século XIX.<ref name="Ewald_2018">{{Citar web|ultimo=Ewald|primeiro=William|url=https://plato.stanford.edu/entries/settheory-early/|titulo=The Emergence of First-Order Logic|data=17 de novembro de 2018|acessodata=2 de novembro de 2022|website=Stanford Encyclopedia of Philosophy|arquivourl=https://web.archive.org/web/20210512135148/https://plato.stanford.edu/entries/settheory-early/|arquivodata=12 de maio de 2021|urlmorta=live}}</ref><ref name="Ferreirós_2020">{{Citar web|ultimo=Ferreirós|primeiro=José|url=https://plato.stanford.edu/entries/settheory-early/|titulo=The Early Development of Set Theory|data=18 de junho de 2020|acessodata=2 de novembro de 2022|website=Stanford Encyclopedia of Philosophy|arquivourl=https://web.archive.org/web/20210512135148/https://plato.stanford.edu/entries/settheory-early/|arquivodata=12 de maio de 2021|urlmorta=live}}</ref> Antes deste período, os [[conjuntos]] não eram considerados objetos matemáticos, e a [[lógica]], embora usada em [[Prova matemática|provas matemáticas]], pertencia à [[filosofia]] e não era estudada especificamente pelos matemáticos.<ref>{{Citar periódico |url=https://idus.us.es/xmlui/bitstream/11441/38373/1/The%20road%20to%20modern%20logic.pdf |título=The Road to Modern Logic—An Interpretation |data=2001 |acessodata=11 de novembro de 2022 |periódico=Bulletin of Symbolic Logic |número=4 |ultimo=Ferreirós |primeiro=José |paginas=441–484 |doi=10.2307/2687794 |jstor=2687794 |arquivourl=https://web.archive.org/web/20230202133703/https://idus.us.es/bitstream/handle/11441/38373/The%20road%20to%20modern%20logic.pdf?sequence=1 |arquivodata=2 de fevereiro de 2023 |volume=7}}</ref> |
|||
Antes do estudo de [[Georg Cantor|Cantor]] sobre [[Conjunto infinito|conjuntos infinitos]], os matemáticos relutavam em considerar coleções [[Infinito atual|realmente infinitas]] e consideravam o [[infinito]] o resultado de [[Enumeração|uma enumeração]] infinita. O trabalho de Cantor ofendeu muitos matemáticos não apenas por considerar conjuntos realmente infinitos,<ref>{{Citar web|ultimo=Wolchover|primeiro=Natalie|autorlink=Natalie Wolchover|url=https://www.scientificamerican.com/article/infinity-logic-law/|titulo=Dispute over Infinity Divides Mathematicians|data=3 de dezembro de 2013|acessodata=1 de novembro de 2022|website=[[Scientific American]]|arquivourl=https://web.archive.org/web/20221102011848/https://www.scientificamerican.com/article/infinity-logic-law/|arquivodata=2 de novembro de 2022|urlmorta=live}}</ref> mas por mostrar que isto implica em diferentes tamanhos de infinito, de acordo com o [[argumento de diagonalização de Cantor]].<ref>{{Citar web|ultimo=Zhuang|primeiro=C.|url=https://philarchive.org/archive/ZHUWAO|titulo=Wittgenstein's analysis on Cantor's diagonal argument|acessodata=18 de novembro de 2022|website=PhilArchive}}</ref> Esta se tornou a crise fundamental da matemática.<ref>{{Citar web|ultimo=Avigad|primeiro=Jeremy|autorlink=Jeremy Avigad|ultimo2=Reck|primeiro2=Erich H.|url=https://www.andrew.cmu.edu/user/avigad/Papers/infinite.pdf|titulo="Clarifying the nature of the infinite": the development of metamathematics and proof theory|data=11 de dezembro de 2001|acessodata=12 de novembro de 2022|website=Carnegie Mellon Technical Report CMU-PHIL-120|arquivourl=https://web.archive.org/web/20221009074025/https://www.andrew.cmu.edu/user/avigad/Papers/infinite.pdf|arquivodata=9 de outubro de 2022|urlmorta=live}}</ref> Posteriormente, este problema foi resolvido na matemática convencional, ao sistematizar o método axiomático dentro de uma [[Axiomas de Zermelo-Fraenkel|teoria de conjuntos formalizada]]. A grosso modo, cada objeto matemático é definido pelo conjunto de todos os objetos semelhantes e pelas propriedades que esses objetos devem ter.<ref name="Warner_2013"/> Por exemplo, na [[Axiomas de Peano|aritmética de Peano]], os [[números naturais]] são definidos por "zero é um número", "cada número tem um sucessor único", "cada número exceto zero tem um antecessor único" e algumas regras de [[raciocínio]].<ref>{{Citar livro|url={{GBurl|id=OXfmTHXvRXMC|p=3}}|título=Numbers, Sets and Axioms: The Apparatus of Mathematics|ultimo=Hamilton|primeiro=Alan G.|editora=Cambridge University Press|ano=1982|páginas=3–4|isbn=978-0-521-28761-6|acessodata=12 de novembro de 2022}}</ref> Esta [[Abstração (matemática)|abstração matemática]] da realidade está incorporada na filosofia moderna do [[Objeto formal|formalismo]], fundada por [[David Hilbert]] por volta de 1910.<ref name="Snapper">{{Citar periódico |título=The Three Crises in Mathematics: Logicism, Intuitionism, and Formalism |data=Setembro de 1979 |periódico=Mathematics Magazine |número=4 |ultimo=Snapper |primeiro=Ernst |autorlink=Ernst Snapper |paginas=207–216 |doi=10.2307/2689412 |jstor=2689412 |volume=52}}</ref> |
|||
O estudo de quantidades começa com os [[número]]s, primeiro os familiares [[número natural|números naturais]], depois os [[número inteiro|inteiros]], e as operações aritméticas com eles, que é chamada de [[aritmética]]. As propriedades dos números inteiros são estudadas na [[teoria dos números]], dentre eles o popular [[Último Teorema de Fermat]]. A teoria dos números também inclui dois grandes problemas que ainda não foram resolvidos: [[conjectura dos primos gêmeos]] e [[conjectura de Goldbach]]. |
|||
A "natureza" dos objetos definidos desta forma é um problema filosófico que os matemáticos deixam para os filósofos, mesmo que muitos matemáticos tenham opiniões{{Mdash}} por vezes chamada de "intuições" {{Mdash}} sobre isto e as usem para orientar o seu estudo e provas. A abordagem permite considerar "lógicas" (isto é, conjuntos de regras de dedução permitidas), teoremas, provas, etc, como objetos matemáticos e, assim, provar teoremas sobre eles. Por exemplo, os [[teoremas da incompletude de Gödel]] afirmam, a grosso modo, que, em todo [[sistema formal]] [[Consistência|consistente]] que contém os números naturais, existem teoremas que são verdadeiros (que são demonstráveis num sistema mais forte), mas não demonstráveis dentro do sistema.<ref name="Raatikainen_2005">{{Citar periódico |url=https://www.cairn.info/revue-internationale-de-philosophie-2005-4-page-513.htm |título=On the Philosophical Relevance of Gödel's Incompleteness Theorems |data=Outubro de 2005 |acessodata=12 de novembro de 2022 |periódico=Revue Internationale de Philosophie |número=4 |ultimo=Raatikainen |primeiro=Panu |paginas=513–534 |doi=10.3917/rip.234.0513 |jstor=23955909 |arquivourl=https://web.archive.org/web/20221112212555/https://www.cairn.info/revue-internationale-de-philosophie-2005-4-page-513.htm |arquivodata=12 de novembro de 2022 |volume=59}}</ref> Esta abordagem aos fundamentos da matemática foi desafiada durante a primeira metade do século XX por matemáticos liderados por [[Luitzen Egbertus Jan Brouwer|Brouwer]], que promoveram a [[lógica intuicionista]], que carece explicitamente da [[lei do terceiro excluído]].<ref>{{Citar web|ultimo=Moschovakis|primeiro=Joan|autorlink=Joan Moschovakis|url=https://plato.stanford.edu/entries/logic-intuitionistic/|titulo=Intuitionistic Logic|data=4 de setembro de 2018|acessodata=12 de novembro de 2022|website=Stanford Encyclopedia of Philosophy|arquivourl=https://web.archive.org/web/20221216154821/https://plato.stanford.edu/entries/logic-intuitionistic/|arquivodata=16 de dezembro de 2022|urlmorta=live}}</ref><ref>{{Citar periódico |título=At the Heart of Analysis: Intuitionism and Philosophy |periódico=Philosophia Scientiæ, Cahier spécial 6 |ultimo=McCarty |primeiro=Charles |ano=2006 |paginas=81–94 |doi=10.4000/philosophiascientiae.411 |doi-access=free}}</ref> Estes problemas e debates acadêmicos levaram a uma ampla expansão da abrangência da lógica matemática, com o surgimento de subáreas como [[teoria dos modelos]] (modelagem de algumas teorias lógicas dentro de outras teorias), [[teoria da prova]], [[teoria dos tipos]], [[teoria da computabilidade]] e [[teoria da complexidade computacional]].<ref name="MSC">{{Citar web|url=https://zbmath.org/static/msc2020.pdf|titulo=MSC2020-Mathematics Subject Classification System|acessodata=3 de fevereiro de 2024|website=zbMath|publicado=Associate Editors of Mathematical Reviews and zbMATH|arquivourl=https://web.archive.org/web/20240102023805/https://zbmath.org/static/msc2020.pdf|arquivodata=2 de janeiro de 2024|urlmorta=live}}</ref> Embora estes aspectos da lógica matemática tenham sido introduzidos antes do surgimento dos [[Computador|computadores]], a sua utilização no design de [[Compilador|compiladores]], [[Programa de computador|certificação de programas]] e outros aspectos da [[ciência da computação]], contribuíram para a expansão destas teorias lógicas.<ref>{{Citar web|ultimo=Halpern|primeiro=Joseph|ultimo2=Harper|primeiro2=Robert|url=https://www.cs.cmu.edu/~rwh/papers/unreasonable/basl.pdf|titulo=On the Unusual Effectiveness of Logic in Computer Science|data=2001|acessodata=15 de janeiro de 2021|arquivourl=https://web.archive.org/web/20210303115643/https://www.cs.cmu.edu/~rwh/papers/unreasonable/basl.pdf|arquivodata=3 de março de 2021|urlmorta=live|ultimo3=Immerman|primeiro3=Neil|ultimo4=Kolaitis|primeiro4=Phokion|ultimo5=Vardi|primeiro5=Moshe|ultimo6=Vianu|primeiro6=Victor}}</ref> |
|||
Conforme o sistema de números foi sendo desenvolvido, os números inteiros foram considerados como um [[subconjunto]] dos [[número racional|números racionais]]. Esses, por sua vez, estão contidos dentro dos [[número real|números reais]], que são usados para representar [[função contínua|quantidades contínuas]]. Números reais são parte dos [[número complexo|números complexos]]. Esses são os primeiros passos da hierarquia dos números que segue incluindo [[quaterniões]] e [[octoniões]]. |
|||
=== Estatísticas e outras ciências de decisão === |
|||
Considerações sobre os números naturais levaram aos [[Número transfinito|números transfinitos]], que formalizam o conceito de contar até o [[infinito]]. Outra área de estudo é o tamanho, que levou aos [[número cardinal|números cardinais]] e então a outro conceito de infinito: os [[Aleph (matemática)|números Aleph]], que permitem uma comparação entre o tamanho de conjuntos infinitamente largos. |
|||
{{AP|Estatística}} |
|||
{{Quote|Algo se torna objetivo (em oposição a "subjetivo") assim que estamos convencidos de que existe nas mentes dos outros da mesma forma que existe nas nossas e que podemos pensar sobre isso e discuti-lo juntos.<ref>Ver {{cite journal |
|||
| first=L. | last=White | year=1947 |
|||
| title=The locus of mathematical reality: An anthropological footnote |
|||
| journal=Philosophy of Science |
|||
| volume=14|issue=4 | pages=289–303 |
|||
| doi=10.1086/286957 | s2cid=119887253 |
|||
| id=189303 | postscript=; |
|||
}} also in {{cite book |
|||
| first=J. R. | last=Newman | year=1956 |
|||
| title=The World of Mathematics |
|||
| publisher=Simon and Schuster | location=New York |
|||
| volume=4 | pages=2348–2364 |
|||
}}</ref> Como a linguagem da matemática é tão precisa, ela é ideal para definir conceitos para os quais existe tal consenso. Na minha opinião, isso é suficiente para nos fornecer um sentimento de uma existência objetiva, de uma realidade matemática...}} |
|||
[[Ficheiro:IllustrationCentralTheorem.png|miniaturadaimagem|Qualquer que seja a forma de uma [[Distribuição de probabilidade|distribuição]] populacional aleatória (μ), a média amostral (x̄) tende para uma distribuição gaussiana e sua [[variância]] (σ) é dada pelo [[teorema central do limite]] da [[teoria das probabilidades]].<ref>{{Citar livro|url=http://www.incertitudes.fr/book.pdf|título=Probability, Statistics and Estimation|ultimo=Rouaud|primeiro=Mathieu|data=Abril de 2017|acessodata=13 de fevereiro de 2024|arquivourl=https://ghostarchive.org/archive/20221009/http://www.incertitudes.fr/book.pdf|arquivodata=9 de outubro de 2022}}</ref>]] |
|||
O campo de estudo da [[estatística]] é uma aplicação matemática empregada para a coleta e o processamento de amostras de dados, por meio do uso de procedimentos baseados em métodos matemáticos, especialmente a [[teoria das probabilidades]]. Os estatísticos geram dados com experimentos ou [[Amostragem (estatística)|amostragem aleatória]],<ref>{{Citar livro|título=Statistics and Truth: Putting Chance to Work|ultimo=Rao|primeiro=C. Radhakrishna|editora=World Scientific|ano=1997|páginas=3–17, 63–70|isbn=981-02-3111-3|lccn=97010349|mr=1474730|oclc=36597731|edição=2nd}}</ref> cujo desenho determina os métodos analíticos que serão utilizados. A análise dos dados de [[Ciência observacional|estudos observacionais]] é feita pela utilização de [[Modelo estatístico|modelos estatísticos]] e da teoria da [[Inferência estatística|inferência]], por meio de modelos de seleção e [[Teoria da estimativa|estimativa]]. Os modelos e as [[Método científico|previsões]] consequentes devem então ser [[Testes de hipóteses|testados]] em relação a [[Método científico|novos dados]].{{Nre|Como outras ciências matemáticas, como [[física]] e [[ciência da computação]], a estatística é uma disciplina autônoma e não um ramo da matemática aplicada. Assim como os físicos pesquisadores e os cientistas da computação, os estatísticos pesquisadores são cientistas matemáticos. Muitos estatísticos são formados em matemática e alguns estatísticos também são matemáticos.}} |
|||
{| style="border:1px solid #ddd; text-align:center; margin: auto;" cellspacing="20" |
|||
| <math>1, 2, 3, \ldots</math> || <math>0, 1, -1, \ldots</math> || <math>\frac{1}{2}, \frac{2}{3}, 0.125,\ldots</math> || <math>\pi, e, \sqrt{2}, \frac{2}{3}, -1,\ldots</math> || <math> i, 1+i, 2e^{i\pi/3},\ldots </math> |
|||
|- |
|||
| [[número natural|Números naturais]] || [[número inteiro|Números inteiros]] || [[número racional|Números racionais]] || [[número real|Números reais]] || [[número complexo|Números complexos]] |
|||
|- |
|||
||<math>+,-,\times,\div</math>||<math>\pi</math>||<math>\omega, \omega + 1, \ldots, 2\omega, \ldots</math> || <math>\aleph_0</math> |
|||
|- |
|||
||[[Aritmética]] || [[Constante matemática]] || [[Número ordinal]] || [[Número cardinal]] |
|||
|} |
|||
A teoria estatística estuda [[Teoria da decisão|problemas de decisão]] como a minimização do [[Risco (administração)|risco]] de uma ação estatística ao usar um [[Estatística|procedimento]], por exemplo, [[Teoria da estimativa|estimativa de parâmetros]], [[Testes de hipóteses|teste de hipóteses]] e [[algoritmo de seleção|seleção de algoritimos]]. Nestas áreas tradicionais da [[estatística matemática]], um problema de decisão estatística é formulado minimizando uma [[função de perda]] sob restrições específicas. Por exemplo, conceber uma pesquisa estatística frequentemente envolve minimizar o custo de estimar a média da população com alguma confiança.<ref name="RaoOpt">{{Citar livro|título=Mathematical programming in statistics|ultimo=Rao|primeiro=C. Radhakrishna|editora=Wiley|ano=1981|editor-sobrenome=Arthanari|series=Wiley Series in Probability and Mathematical Statistics|localização=New York|páginas=vii–viii|capitulo=Foreword|isbn=978-0-471-08073-2|lccn=80021637|mr=607328|oclc=6707805|editor-sobrenome2=Dodge|editor-link2=Yadolah Dodge}}</ref> Devido ao uso da [[otimização]], a teoria estatística se sobrepõe a outras [[Teoria da decisão|ciências da decisão]], como a [[Investigação operacional|pesquisa operacional]], a [[teoria do controle]] e a [[economia matemática]].{{Sfn|Whittle|1994|pp=10–11, 14–18}} |
|||
==== Estrutura ==== |
|||
Muitos objetos matemáticos, tais como [[conjunto]]s de números e [[Função (matemática)|funções matemáticas]], exibem uma estrutura interna. As propriedades estruturais desses objetos são investigadas através do estudo de [[Grupo (matemática)|grupos]], [[anel (matemática)|anéis]], [[corpo]]s e outros sistemas abstratos, que são eles mesmos tais objetos. Este é o campo da [[álgebra abstrata]]. Um conceito importante é a noção de vetor, que se generaliza quando são estudados os [[espaço vetorial]] em [[álgebra linear]]. O estudo de vetores combina três das áreas fundamentais da matemática: quantidade, estrutura e espaço. |
|||
=== Matemática computacional === |
|||
{| style="border:1px solid #ddd; text-align:center; margin: auto;" cellspacing="20" |
|||
{{AP|Matemática computacional}} |
|||
| [[Imagem:Rubik's cube.svg|96px]] || [[Imagem:Matrix multiplication diagram.PNG|96px]] ||[[Imagem:Lattice of the divisibility of 60.svg|96px]] || [[Imagem:6n-graf.svg|128px]] || <math>(()(()()))</math> |
|||
A [[matemática computacional]] é o estudo de [[Problema matemático|problemas matemáticos]] que normalmente são grandes demais para a capacidade numérica dos seres humanos.<ref>{{Citar web|ultimo=Marchuk|primeiro=Gurii Ivanovich|url=https://mathshistory.st-andrews.ac.uk/Extras/Computational_mathematics/|titulo=G I Marchuk's plenary: ICM 1970|data=abril de 2020|acessodata=13 de novembro de 2022|publicado=School of Mathematics and Statistics, University of St Andrews, Scotland|arquivourl=https://web.archive.org/web/20221113155409/https://mathshistory.st-andrews.ac.uk/Extras/Computational_mathematics/|arquivodata=13 de novembro de 2022|urlmorta=live}}</ref><ref>{{cite conference | title=Grand Challenges, High Performance Computing, and Computational Science | last1=Johnson | first1=Gary M. | last2=Cavallini | first2=John S. | conference=Singapore Supercomputing Conference'90: Supercomputing For Strategic Advantage | date=Setembro de 1991 | page=28 |lccn=91018998 |publisher=World Scientific | editor1-first=Kang Hoh | editor1-last=Phua | editor2-first=Kia Fock | editor2-last=Loe | url={{GBurl|id=jYNIDwAAQBAJ|p=28}} | access-date=13 de novembro de 2022 }}</ref> A [[análise numérica]] estuda métodos para problemas de [[Análise matemática|análise]] utilizando a [[análise funcional]] e a [[Teoria da aproximação|teoria de aproximação]]; a análise numérica inclui o estudo de [[aproximação]] e [[discretização]] com foco especial em [[Erro de arredondamento|erros de arredondamento]].<ref>{{cite book |last=Trefethen |first=Lloyd N. |editor1-last=Gowers |editor1-first=Timothy |editor2-last=Barrow-Green |editor2-first=June |editor2-link=June Barrow-Green |editor3-last=Leader |editor3-first=Imre |year=2008 |chapter=Numerical Analysis |pages=604–615 |title=The Princeton Companion to Mathematics |publisher=[[Princeton University Press]] |isbn=978-0-691-11880-2 |lccn=2008020450 |mr=2467561 |oclc=227205932 |url=http://people.maths.ox.ac.uk/trefethen/NAessay.pdf |url-status=live |archive-url=https://web.archive.org/web/20230307054158/http://people.maths.ox.ac.uk/trefethen/NAessay.pdf |archive-date=7 de março de 2023 |access-date=15 de fevereiro de 2024}}</ref> |
|||
|- |
|||
| [[Álgebra abstrata]] || [[Álgebra linear]] || [[Teoria da ordem]] || [[Teoria dos grafos]] || [[Teoria dos operadores]] |
|||
|} |
|||
== História == |
|||
{{AP|História da matemática}} |
|||
{{Artigo principal|Espaço matemático}} |
|||
=== Antiguidade === |
|||
O estudo do espaço originou-se com a [[geometria]]<ref>{{citar web|url=http://revistaescola.abril.com.br/matematica/pratica-pedagogica/direcao-dimensao-428166.shtml|publicado=NOVA ESCOLA|titulo=Mostre aos alunos os conceitos de direção e dimensão|acessodata=17 de maio de 2009|arquivourl=https://web.archive.org/web/20090429030500/http://revistaescola.abril.com.br/matematica/pratica-pedagogica/direcao-dimensao-428166.shtml#|arquivodata=29 de abril de 2009|urlmorta=yes}}</ref> - em particular, com a [[geometria euclidiana]]. [[Trigonometria]] combina o [[Espaço matemático|espaço]] e os [[número]]s, e contém o famoso [[teorema de Pitágoras]]. O estudo moderno do espaço generaliza essas ideias para incluir geometria de dimensões maiores, geometria não-euclidiana (que tem papel central na [[relatividade geral]]) e [[Topologia (matemática)|topologia]]. Quantidade e espaço juntos fazem a [[geometria analítica]], [[geometria diferencial]], e [[geometria algébrica]]. |
|||
[[Imagem:Plimpton_322.jpg|miniaturadaimagem| A tabuleta matemática babilônica ''[[Plimpton 322]]'', datada de 1800 a.C.]] |
|||
[[Imagem:Egyptian A'h-mosè or Rhind Papyrus (1065x1330).png|thumb|[[Papiro de Rhind]], um documento antigo contendo [[Problema matemático|problemas matemáticos]]]] |
|||
A [[história da matemática]] é uma série cada vez maior de [[Abstração (matemática)|abstrações]]. Evolutivamente falando, a primeira abstração a ser descoberta, compartilhada por muitos animais,<ref>{{Citar periódico |título=Abstract representations of numbers in the animal and human brain |data=Agosto de 1998 |periódico=Trends in Neurosciences |número=8 |ultimo=Dehaene |primeiro=Stanislas |ultimo2=Dehaene-Lambertz |primeiro2=Ghislaine |paginas=355–361 |doi=10.1016/S0166-2236(98)01263-6 |pmid=9720604 |ultimo3=Cohen |primeiro3=Laurent |volume=21}}</ref> foi provavelmente a dos [[números]]: a constatação de que, por exemplo, uma coleção de duas maçãs e uma coleção de duas laranjas (digamos) têm algo em comum, nomeadamente que existem ''duas'' delas. Além de reconhecerem como [[Contagem (matemática)|contar]] objetos físicos, os povos [[Pré-história|pré-históricos]] também podem ter sabido contar quantidades abstratas, como o [[tempo]] {{Mdash}} [[dias]], [[Estação do ano|estações]] ou [[Ano|anos]].<ref>See, for example, {{Citar livro|título=Evolution of Mathematical Concepts; an Elementary Study|ultimo=Wilder|primeiro=Raymond L.|autorlink=Raymond L. Wilder}}</ref><ref>{{Citar livro|título=Africa Counts: Number and Pattern in African Culture.|ultimo=Zaslavsky|primeiro=Claudia|data=1999|editora=Chicago Review Press|isbn=978-1-61374-115-3|oclc=843204342|autorlink=Claudia Zaslavsky}}</ref> |
|||
{| style="border:1px solid #ddd; text-align:center; margin: auto;" cellspacing="20" |
|||
| [[Imagem:Torus.jpg|128px]] || [[Imagem:Pythagorean.svg|128px]] || [[Imagem:Sin.svg|160px]] || [[Imagem:Osculating circle.svg|128px]] || [[Imagem:Koch curve.png|128px]] |
|||
|- |
|||
| [[Topologia (matemática)|Topologia]] || [[Geometria]] || [[Trigonometria]] || [[Geometria diferencial]] || [[Geometria fractal]] |
|||
|} |
|||
As primeiras evidências de matemática mais complexa só começam a aparecer por volta de 3.000 a.C., quando os povos [[Civilização babilônica|babilônios]] e [[Antigo Egito|egípcios]] iniciam o uso de [[aritmética]], [[álgebra]] e [[geometria]] para estimar seus impostos e fazer outros cálculos financeiros voltados para construção e astronomia.{{Sfn|Kline|1990|loc=Chapter 1}} Os textos matemáticos mais antigos da [[Mesopotâmia]] e do [[Antigo Egito|Egito]] datam de 2000 a.C. a 1800 a.C.. Muitos textos antigos mencionam [[Terno pitagórico|triplos pitagóricos]] e assim, por inferência, o [[teorema de Pitágoras]] parece ser o conceito matemático mais antigo e difundido depois da aritmética e geometria básicas. É na [[matemática babilônica]] que a [[aritmética elementar]] ([[adição]], [[subtração]], [[multiplicação]] e [[divisão]]) aparece pela primeira vez no [[registro arqueológico]]. Os babilônios também possuíam um sistema de valor posicional e usavam um [[sistema de numeração]] [[Sistema de numeração sexagesimal|sexagesimal]] que ainda é usado atualmente para medir [[Ângulo|ângulos]] e o tempo.{{Sfn|Boyer|1991|loc="Mesopotamia" pp. 24–27}} |
|||
==== Transformações ==== |
|||
Entender e descrever uma transformação é um tema comum na [[ciência natural]] e o [[cálculo]] foi desenvolvido como uma poderosa ferramenta para investigar isso. Então as [[Função (matemática)|funções]] foram criadas, como um conceito central para descrever uma quantidade que muda com o passar do tempo. O rigoroso estudo dos [[número real|números reais]] e funções reais são conhecidos como [[análise real]], e a [[análise complexa]] a equivalente para os [[número complexo|números complexos]]. |
|||
No [[século VI a.C.]], a [[matemática grega]] começou a emergir como uma disciplina distinta e alguns [[Grécia Antiga|gregos antigos]], como os [[Escola pitagórica|pitagóricos]], pareciam tê-la considerado um assunto por direito próprio.<ref>{{Citar livro|url=https://archive.org/details/historyofgreekma0002heat/page/n14|título=A History of Greek Mathematics: From Thales to Euclid|ultimo=Heath|primeiro=Thomas Little|data=1981|editora=Dover Publications|localização=New York|isbn=978-0-486-24073-2}}</ref> Por volta do ano 300 a.C., [[Euclides]] organizou o conhecimento matemático por meio de postulados e primeiros princípios, que evoluíram para o método axiomático usado atualmente na matemática, que consiste em definição, axioma, teorema e prova matemáticas.<ref>{{Citar periódico |título=Euclid's Elements and the Axiomatic Method |data=1969 |periódico=The British Journal for the Philosophy of Science |número=4 |ultimo=Mueller |primeiro=I. |paginas=289–309 |doi=10.1093/bjps/20.4.289 |issn=0007-0882 |jstor=686258 |volume=20}}</ref> Sua obra, ''[[Os Elementos]]'', é amplamente considerada o [[livro didático]] de maior sucesso e influência de todos os tempos.{{Sfn|Boyer|1991|loc="Euclid of Alexandria" p. 119}} O maior matemático da antiguidade é frequentemente considerado [[Arquimedes]] ({{Circa|287|212 BC}}) de [[Siracusa]].{{Sfn|Boyer|1991|loc="Archimedes of Syracuse" p. 120}} Ele desenvolveu fórmulas para calcular a área superficial e o volume de [[Sólido de revolução|sólidos de revolução]] e usou o [[método da exaustão]] para calcular a [[área]] sob o arco de uma [[parábola]] com a [[Série (matemática)|soma de uma série infinita]], de uma maneira não muito diferente do cálculo moderno.{{Sfn|Boyer|1991|loc="Archimedes of Syracuse" p. 130}} Outras conquistas notáveis da matemática grega são [[Cónica|seções cônicas]] ([[Apolônio de Perga]], século III a.C.),{{Sfn|Boyer|1991|loc="Apollonius of Perga" p. 145}} [[trigonometria]] ([[Hiparco|Hiparco de Nicéia]], século II a.C.){{Sfn|Boyer|1991|loc="Greek Trigonometry and Mensuration" p. 162}} e os primórdios da álgebra ([[Diofanto]], século III d.C.).{{Sfn|Boyer|1991|loc="Revival and Decline of Greek Mathematics" p. 180}} |
|||
A [[hipótese de Riemann]], uma das mais fundamentais perguntas não respondidas da matemática, é baseada na análise complexa. [[Análise funcional]] se foca no [[Espaço matemático|espaço]] das funções. Uma das muitas aplicações da análise funcional é a [[mecânica quântica]]. Muitos problemas levaram naturalmente a relações entre a quantidade e sua taxa de mudança e esses problemas são estudados nas [[equação diferencial|equações diferenciais]]. Muitos fenômenos da natureza podem ser descritos pelos [[sistema dinâmico|sistemas dinâmicos]]; a [[teoria do caos]] descreve com precisão os modos com que muitos sistemas exibem um padrão imprevisível, porém ainda assim determinístico. |
|||
[[Ficheiro:Bakhshali_numerals_2.jpg|direita|miniaturadaimagem| Os numerais usados no [[Manuscrito Bakhshali]], datados entre o século II a.C. e o século II d.C.]] |
|||
O [[Sistema numérico hindu-arábico|sistema de numeração hindu-arábico]] e as regras para o uso de suas operações, em uso atualmente em todo o planeta, evoluíram no decorrer do [[primeiro milênio]] na [[Matemática indiana|Índia]] e foram transmitidos ao [[mundo ocidental]] através da [[matemática islâmica]].<ref>{{Citar livro|url={{GBurl|id=Sl_6BPp7S0AC|pg=IA19}}|título=Number Theory and Its History|ultimo=Ore|primeiro=Øystein|editora=Courier Corporation|ano=1988|páginas=19–24|isbn=978-0-486-65620-5|autorlink=Øystein Ore|acessodata=14 de novembro de 2022}}</ref> Outros desenvolvimentos notáveis da [[matemática indiana]] incluem a moderna definição e aproximação de [[seno]] e [[cosseno]], além de uma forma inicial de [[Série (matemática)|séries infinitas]].<ref>{{Citar periódico |título=On the Use of Series in Hindu Mathematics |data=Janeiro de 1936 |periódico=Osiris |ultimo=Singh |primeiro=A. N. |paginas=606–628 |doi=10.1086/368443 |jstor=301627 |volume=1}}</ref><ref>{{Citar livro|título=Studies in Indian Mathematics and Astronomy|ultimo=Kolachana|primeiro=A.|ultimo2=Mahesh|primeiro2=K.|ultimo3=Ramasubramanian|primeiro3=K.|editora=Springer|ano=2019|series=Sources and Studies in the History of Mathematics and Physical Sciences|páginas=438–461|capitulo=Use of series in India|doi=10.1007/978-981-13-7326-8_20|isbn=978-981-13-7325-1|local-publicação=Singapore}}</ref> |
|||
=== Medieval e posterior === |
|||
{| style="border:1px solid #ddd; text-align:center; margin: auto;" cellspacing="20" |
|||
[[Ficheiro:Image-Al-Kitāb_al-muḫtaṣar_fī_ḥisāb_al-ğabr_wa-l-muqābala.jpg|miniaturadaimagem| Uma página da obra ''Álgebra'' de [[Alcuarismi]]]] |
|||
| [[Imagem:Integral as region under curve.svg|128px]] || [[Imagem:Vector field.svg|128px]] || [[Imagem:Airflow-Obstructed-Duct.png|128px]] || [[Imagem:Limitcycle.jpg|128px]] || [[Imagem:Lorenz attractor.svg|128px]] |
|||
Durante a [[Idade de ouro islâmica|Idade de Ouro Islâmica]], especialmente durante os séculos IX e X, a [[matemática islâmica]] desenvolveu várias inovações importantes baseadas na [[matemática grega]]. A conquista mais notável da matemática islâmica foi o desenvolvimento da [[álgebra]]. Outras conquistas do período islâmico incluem avanços na [[trigonometria esférica]] e a adição do [[Separador decimal|ponto decimal]] ao [[Algarismos arábicos|sistema de numeração arábico]].<ref>{{Citar livro|título=A history of Arabic astronomy: planetary theories during the golden age of Islam|ultimo=Saliba|primeiro=George|data=1994|editora=New York University Press|isbn=978-0-8147-7962-0|oclc=28723059|autorlink=George Saliba}}</ref> Muitos matemáticos notáveis deste período eram persas, como [[Alcuarismi]], [[Omar Caiam]] e [[Xarafadim de Tus]].<ref>{{Citar periódico |url=https://eric.ed.gov/?id=EJ854295 |título=Contributions of Islamic scholars to the scientific enterprise |acessodata=14 de novembro de 2022 |periódico=International Education Journal |publicado=Shannon Research Press |número=4 |ultimo=Faruqi |primeiro=Yasmeen M. |ano=2006 |paginas=391–399 |arquivourl=https://web.archive.org/web/20221114165547/https://eric.ed.gov/?id=EJ854295 |arquivodata=14 de novembro de 2022 |volume=7}}</ref> Os textos matemáticos gregos e árabes foram, por sua vez, traduzidos para o [[latim]] durante a [[Idade Média]] e reintroduzidos na [[Europa]]. <ref>{{Citar periódico |url=https://epub.ub.uni-muenchen.de/15929/1/greek-arabic-latin.pdf |título=Greek-Arabic-Latin: The Transmission of Mathematical Texts in the Middle Ages |data=Junho de 2001 |acessodata=5 de dezembro de 2022 |periódico=Science in Context |publicado=Cambridge University Press |número=1–2 |ultimo=Lorch |primeiro=Richard |paginas=313–331 |doi=10.1017/S0269889701000114 |arquivourl=https://web.archive.org/web/20221217160922/https://epub.ub.uni-muenchen.de/15929/1/greek-arabic-latin.pdf |arquivodata=17 de dezembro de 2022 |volume=14}}</ref> |
|||
|- |
|||
| [[Cálculo]] ||[[Cálculo vetorial]] || [[Equação diferencial|Equações diferenciais]] || [[Sistema dinâmico]] || [[Teoria do caos]] |
|||
|} |
|||
No início da [[Idade Moderna]], a matemática começou a desenvolver-se em ritmo acelerado na [[Europa Ocidental]], com inovações revolucionárias, como a introdução de [[Variável (matemática)|variáveis]] e da [[Matemática|notação simbólica]] pelo francês [[François Viète]] (1540–1603), a introdução de [[logaritmos]] pelo escocês [[John Napier]] em 1614, que simplificou bastante os cálculos numéricos, especialmente para [[astronomia]] e [[navegação marítima]], a introdução de [[Sistema de coordenadas|coordenadas]] pelo francês [[René Descartes]] (1596-1650) para reduzir a geometria à álgebra, além do desenvolvimento do cálculo pelo inglês [[Isaac Newton]] (1642-1726/27) e pelo alemão [[Gottfried Wilhelm Leibniz|Gottfried Leibniz]] (1646–1716). O suíço [[Leonhard Euler]] (1707-1783), o mais notável matemático do século XVIII, unificou todas estas inovações com uma terminologia padronizada e completou-as com a descoberta e a prova de vários teoremas.<ref name="volumes">{{citar periódico|sobrenome= Finkel|nome= B.F.|ano= 1897|título= Biography- Leonard Euler|periódico= The American Mathematical Monthly|volume= 4|número= 12|páginas= 300}}</ref> |
|||
=== Matemática discreta === |
|||
[[Ficheiro:Carl_Friedrich_Gauss_1840_by_Jensen.jpg|miniaturadaimagem|[[Carl Friedrich Gauss|Carlos Friedrich Gauss]]]] |
|||
[[Matemática discreta]] é o nome comum para o campo da matemática mais geralmente usado na [[teoria da computação]]. Isso inclui a [[computabilidade]], [[complexidade computacional]] e [[teoria da informação]]. Computabilidade examina as limitações dos vários modelos teóricos do computador, incluindo o mais poderoso modelo conhecido - a [[máquina de Turing]]. |
|||
Talvez o principal matemático do século XIX tenha sido o alemão [[Carl Gauss]], conhecido por ter feito inúmeras contribuições nos mais variados campos, como [[álgebra]], [[análise]], [[geometria diferencial]], [[Matriz (matemática)|teoria das matrizes]], [[teoria dos números]] e [[estatística]].<ref>{{Citar periódico |título=History of Mathematics After the Sixteenth Century |data=Janeiro de 1949 |periódico=The American Mathematical Monthly |número=1 |ultimo=Archibald |primeiro=Raymond Clare |autorlink=Raymond Clare Archibald |series=Part 2: Outline of the History of Mathematics |paginas=35–56 |doi=10.2307/2304570 |jstor=2304570 |volume=56}}</ref> Já no início do século XX, o austríaco [[Kurt Gödel]] transformou a matemática ao publicar os seus [[Teoremas da incompletude de Gödel|teoremas da incompletude]], que mostram em parte que qualquer sistema axiomático consistente {{Mdash}} se for suficientemente poderoso para descrever a aritmética {{Mdash}} conterá proposições verdadeiras que não podem ser provadas.<ref name="Raatikainen_2005">{{Citar periódico |url=https://www.cairn.info/revue-internationale-de-philosophie-2005-4-page-513.htm |título=On the Philosophical Relevance of Gödel's Incompleteness Theorems |data=Outubro de 2005 |acessodata=12 de novembro de 2022 |periódico=Revue Internationale de Philosophie |número=4 |ultimo=Raatikainen |primeiro=Panu |paginas=513–534 |doi=10.3917/rip.234.0513 |jstor=23955909 |arquivourl=https://web.archive.org/web/20221112212555/https://www.cairn.info/revue-internationale-de-philosophie-2005-4-page-513.htm |arquivodata=12 de novembro de 2022 |volume=59}}</ref> |
|||
{| style="border:1px solid #ddd; text-align:center; margin: auto;" cellspacing="20" |
|||
| [[Imagem:Elliptic curve simple.png|96px]] || <math>\begin{matrix} (1,2,3) & (1,3,2) \\ (2,1,3) & (2,3,1) \\ (3,1,2) & (3,2,1) \end{matrix}</math> || [[Imagem:DFAexample.svg|128px]] || [[Imagem:Caesar3.svg|128px]] || [[Imagem:6n-graf.svg|128px]] |
|||
|- |
|||
| [[Teoria de números]] ||[[Combinatória]] || [[Teoria da computação]] || [[Criptografia]] || [[Teoria de grafos]] |
|||
|} |
|||
Desde então, a matemática foi bastante ampliada e tem havido uma interação frutífera com as [[Ciência|ciências]], com benefícios para ambas. Descobertas matemáticas continuam a ser feitas até os dias atuais. Por exemplo, de acordo com a edição de janeiro de 2006 do ''Bulletin of the [[American Mathematical Society]]:'' "O número de artigos e livros incluídos no banco de dados da ''[[Mathematical Reviews]]'' desde 1940 (o primeiro ano de operação da ''MR'') é agora superior a 1,9 milhão e mais de 75 mil itens são adicionados ao banco de dados anualmente. A esmagadora maioria dos trabalhos neste oceano contém novos teoremas matemáticos e suas provas."{{Sfn|Sevryuk|2006|pp=101–109}} |
|||
=== Matemática aplicada === |
|||
[[Matemática aplicada]] considera o uso de ferramentas abstratas de matemática para resolver problemas concretos na [[ciência]], [[negócio]]s e outras áreas. Um importante campo na matemática aplicada é a [[estatística]], que usa a [[teoria das probabilidades]] como uma ferramenta e permite a descrição, análise e predição de fenômenos onde as chances tem um papel fundamental. Muitos estudos de experimentação, acompanhamento e observação requerem um uso de estatísticas. |
|||
== Notação simbólica e terminologia == |
|||
[[Análise numérica]] investiga métodos computacionais para resolver eficientemente uma grande variedade de problemas matemáticos que são tipicamente muito grandes para a capacidade numérica humana; isso inclui estudos de [[erro de arredondamento]] ou outras fontes de erros na computação. |
|||
{{AP|notação matemática}} |
|||
[[Ficheiro:Sigma_summation_notation.svg|miniaturadaimagem| Uma explicação da notação de [[Adição|soma]] sigma (Σ)]] |
|||
A [[notação matemática]] é amplamente utilizada na [[ciência]] e na [[engenharia]] para representar [[Conceito|conceitos]] e [[Propriedade (filosofia)|propriedades]] complexas de forma concisa, inequívoca e precisa. Esta notação consiste em [[Lista de símbolos matemáticos|símbolos]] usados para representar [[Operação (matemática)|operações]], números não especificados, relações e quaisquer outros objetos matemáticos, e depois montá-los em [[Expressão matemática|expressões]] e [[Fórmula matemática|fórmulas]].<ref>{{Citar conferência |ultimo=Wolfram |primeiro=Stephan |autorlink=Stephen Wolfram |url=https://www.stephenwolfram.com/publications/mathematical-notation-past-future/ |titulo=Mathematical Notation: Past and Future |data=outubro de 2000 |acessodata=3 de fevereiro de 2024 |conferencia=MathML and Math on the Web: MathML International Conference 2000, Urbana Champaign, USA |arquivourl=https://web.archive.org/web/20221116150905/https://www.stephenwolfram.com/publications/mathematical-notation-past-future/ |arquivodata=16 de novembro de 2022}}</ref> Mais precisamente, os números e outros objetos matemáticos são representados por símbolos chamados [[Variável (matemática)|variáveis]], que geralmente são letras [[Latim|latinas]] ou [[Alfabeto grego|gregas]]. Operação e relações são geralmente representadas por [[Lista de símbolos matemáticos|símbolos]] ou [[Glifo|glifos]] específicos,<ref>{{Citar periódico |título=Knowledge of Mathematical Symbols Goes Beyond Numbers |data=3 de dezembro de 2020 |periódico=Journal of Numerical Cognition |número=3 |ultimo=Douglas |primeiro=Heather |ultimo2=Headley |primeiro2=Marcia Gail |paginas=322–354 |doi=10.5964/jnc.v6i3.293 |ultimo3=Hadden |primeiro3=Stephanie |ultimo4=LeFevre |primeiro4=Jo-Anne |autorlink4=Jo-Anne LeFevre |volume=6 |doi-access=free}}</ref> como {{Math|+}} ([[Sinais de mais e menos|mais]]), {{Math|×}} ([[Sinal de multiplicação|multiplicação]]), <math display="inline">\int</math> ([[Símbolo integral|integral]]), {{Math|1==}} ([[Sinal de igual|igual]]) e {{Math|<}} ([[menor que]]).<ref name="AMS">{{Citar web|ultimo=Letourneau|primeiro=Mary|ultimo2=Wright Sharp|primeiro2=Jennifer|url=https://www.ams.org/publications/authors/AMS-StyleGuide-online.pdf|titulo=AMS Style Guide|data=outubro de 2017|acessodata=3 de fevereiro de 2024|publicado=[[American Mathematical Society]]|pagina=75|arquivourl=https://web.archive.org/web/20221208063650/https://www.ams.org//publications/authors/AMS-StyleGuide-online.pdf|arquivodata=8 de dezembro de 2022|urlmorta=live}}</ref> Todos esses símbolos são geralmente agrupados de acordo com regras específicas.<ref>{{Citar periódico |url=https://escholarship.org/content/qt35r988q9/qt35r988q9.pdf |título=Constituent Structure in Mathematical Expressions |acessodata=3 de fevereiro de 2024 |periódico=Proceedings of the Annual Meeting of the Cognitive Science Society |publicado=Universidade da Califórnia em Merced|ultimo=Jansen |primeiro=Anthony R. |ultimo2=Marriott |primeiro2=Kim |ano=2000 |oclc=68713073 |arquivourl=https://web.archive.org/web/20221116152222/https://escholarship.org/content/qt35r988q9/qt35r988q9.pdf |arquivodata=16 de novembro de 2022 |ultimo3=Yelland |primeiro3=Greg W. |volume=22}}</ref> |
|||
A matemática desenvolveu uma terminologia rica que cobre uma ampla variedade de campos que estudam as propriedades de vários objetos e suas interações, sendo que fornecem uma base padrão para a comunicação. Um [[axioma]] ou [[Axioma|postulado]], por exemplo, é uma afirmação matemática considerada verdadeira sem necessidade de prova. Se uma afirmação matemática ainda não foi provada (ou refutada), ela é chamada de [[conjectura]]. Através de uma série de argumentos rigorosos empregando [[Método dedutivo|raciocínio dedutivo]], uma afirmação que é [[Derivação formal|comprovadamente]] verdadeira torna-se um teorema. Um teorema especializado usado principalmente para provar outro teorema é chamado de [[Lema (matemática)|lema]]. Um exemplo comprovado que faz parte de uma conclusão mais geral é denominado [[corolário]].<ref>{{Citar livro|título=Theorems, Corollaries, Lemmas, and Methods of Proof|ultimo=Rossi|primeiro=Richard J.|editora=[[John Wiley & Sons]]|ano=2006|series=Pure and Applied Mathematics: A Wiley Series of Texts, Monographs and Tracts|páginas=1–14, 47–48|isbn=978-0-470-04295-3|lccn=2006041609|oclc=64085024}}</ref> |
|||
{| style="border:1px solid #ddd; text-align:center; margin: auto;" cellspacing="20" |
|||
|| [[Imagem:Gravitation space source.png|128px]] |
|||
|| [[Imagem:BernoullisLawDerivationDiagram.svg|128px]] |
|||
|| [[Imagem:Composite trapezoidal rule illustration small.svg|128px]] |
|||
|| [[Imagem:Maximum boxed.png|128px]] |
|||
|- |
|||
| [[Física matemática]] ||[[Mecânica dos fluidos]] || [[Análise numérica]] || [[Otimização]] |
|||
|- |
|||
|| [[Imagem:Two red dice 01.svg|128px]] |
|||
|| [[Imagem:Oldfaithful3.png|128px]] |
|||
|| [[Imagem:Market Data Index NYA on 20050726 202628 UTC.png|128px]] |
|||
|| [[Imagem:Arbitrary-gametree-solved.svg|128px]] |
|||
|- |
|||
| [[Teoria das probabilidades]] ||[[Estatística]] || [[Matemática financeira]] || [[Teoria dos jogos]] |
|||
|} |
|||
Vários termos técnicos usados em matemática são [[Neologismo|neologismos]], como ''[[Polinómio|polinômio]]'' e ''[[homeomorfismo]]''.<ref>{{Citar web|titulo=Earliest Uses of Some Words of Mathematics|acessodata=3 de fevereiro de 2024|publicação=Escócia|publicado=[[Universidade de St. Andrews]]|url=https://web.archive.org/web/20220929032236/https://mathshistory.st-andrews.ac.uk/Miller/mathword/|url=https://mathshistory.st-andrews.ac.uk/Miller/mathword/|arquivodata=29 de setembro de 2022|urlmorta=live}}</ref> Outros termos técnicos são palavras da linguagem comum usadas com um significado preciso que pode diferir ligeiramente do seu significado comum. Por exemplo, em matemática, "[[Disjunção lógica|ou]]" significa "um, o outro ou ambos", enquanto, na linguagem comum, é ambíguo ou significa "um ou outro, mas não ambos" (em matemática, o último é chamado de "[[ou exclusivo]]"). Muitos termos matemáticos são palavras comuns usadas com um significado completamente diferente.<ref>{{Citar periódico |título=The New Language of Mathematics |data=dezembro de 2017 |periódico=The American Scientist |publicado=[[Sigma Xi]] |número=6 |ultimo=Silver |primeiro=Daniel S. |paginas=364–371 |doi=10.1511/2017.105.6.364 |issn=0003-0996 |lccn=43020253 |oclc=1480717 |volume=105 |doi-access=free}}</ref> |
|||
== Matemáticos notáveis == |
|||
{{Artigo principal|prefixo=Ver categoria|[[:Categoria:Matemáticos|Matemáticos]]}} |
|||
== Relação com as ciências == |
|||
<gallery> |
|||
A matemática é usada na maioria das [[ciências]] para [[Modelo (matemática)|modelar]] fenômenos, o que permite que previsões sejam feitas a partir de leis experimentais.<ref>{{Citar livro|url={{GBurl|id=pJAvWaRYo3UC}}|título=Modelling Mathematical Methods and Scientific Computation|ultimo=Bellomo|primeiro=Nicola|ultimo2=Preziosi|primeiro2=Luigi|data=22 de dezembro de 1994|editora=CRC Press|series=Mathematical Modeling|volume=1|isbn=978-0-8493-8331-1|acessodata=16 de novembro de 2022}}</ref> A independência da matemática de qualquer experimentação implica que a precisão de tais previsões depende apenas da adequação do modelo.<ref>{{Citar periódico |url=https://www.researchgate.net/publication/225691477 |título=Mathematical Models and Reality: A Constructivist Perspective |acessodata=17 de novembro de 2022 |periódico=Foundations of Science |ultimo=Hennig |primeiro=Christian |ano=2010 |paginas=29–48 |doi=10.1007/s10699-009-9167-x |volume=15}}</ref> No caso de previsões imprecisas, ao invés delas serem causadas por conceitos matemáticos inválidos, na verdade implicam na necessidade de alteração do modelo utilizado.<ref>{{Citar periódico |url=https://seop.illc.uva.nl/entries/models-science/ |título=Models in Science |data=4 de fevereiro de 2020 |acessodata=17 de novembro de 2022 |periódico=Stanford Encyclopedia of Philosophy |ultimo=Frigg |primeiro=Roman |autorlink=Roman Frigg |ultimo2=Hartmann |primeiro2=Stephan |arquivourl=https://web.archive.org/web/20221117162412/https://seop.illc.uva.nl/entries/models-science/ |arquivodata=17 de novembro de 2022}}</ref> Por exemplo, a [[precessão]] do [[periélio]] do planeta [[Mercúrio (planeta)|Mercúrio]] só pôde ser explicada após o desenvolvimento da [[relatividade geral]] do alemão [[Albert Einstein]], que substituiu a [[lei da gravitação universal]] do inglês [[Isaac Newton]] como um modelo matemático melhor.<ref>{{Citar livro|título=The Map and the Territory: Exploring the Foundations of Science, Thought and Reality|ultimo=Stewart|primeiro=Ian|editora=Springer|ano=2018|editor-sobrenome=Wuppuluri|series=The Frontiers Collection|páginas=345–356|capitulo=Mathematics, Maps, and Models|doi=10.1007/978-3-319-72478-2_18|isbn=978-3-319-72478-2|autorlink=Ian Stewart (mathematician)|acessodata=17 de novembro de 2022|editor-sobrenome2=Doria}}</ref> |
|||
Imagem:Niels Henrik Abel.jpg|[[Niels Henrik Abel|Abel]] |
|||
Imagem:Maria Gaetana Agnesi.jpg|[[Maria Gaetana Agnesi|Agnesi]] |
|||
Imagem:Al-Khwarizmi portrait.jpg|[[Alcuarismi]] |
|||
Imagem:Jean d'Alembert.jpeg|[[Jean le Rond d’Alembert|d’Alembert]] |
|||
Imagem:Domenico-Fetti Archimedes 1620.jpg|[[Arquimedes]] |
|||
Imagem:Hindu astronomer, 19th-century illustration.jpg|[[Brahmagupta]] |
|||
Imagem:Bernard Bolzano.jpg|[[Bernard Bolzano|Bolzano]] |
|||
Imagem:George Boole.jpg|[[George Boole|Boole]] |
|||
Imagem:Georg Cantor2.jpg|[[Georg Cantor|Cantor]] |
|||
Imagem:Augustin-Louis Cauchy 1901.jpg|[[Augustin Louis Cauchy|Cauchy]] |
|||
Imagem:Dedekind.jpeg|[[Richard Dedekind|Dedekind]] |
|||
Imagem:Frans Hals - Portret van René Descartes.jpg|[[René Descartes|Descartes]] |
|||
Imagem:Gotthold Eisenstein.jpeg|[[Gotthold Eisenstein|Eisenstein]] |
|||
Imagem:Erdos head budapest fall 1992.jpg|[[Paul Erdős|Erdős]] |
|||
Imagem:Euclid statue, Oxford University Museum of Natural History, UK - 20080315.jpg|[[Euclides]] |
|||
Imagem:Leonhard Euler.jpg|[[Leonhard Euler|Euler]] |
|||
Imagem:Pierre de Fermat.jpg|[[Pierre de Fermat|Fermat]] |
|||
Imagem:Fibonacci.jpg|[[Leonardo Fibonacci|Fibonacci]] |
|||
Imagem:Evariste galois.jpg|[[Évariste Galois|Galois]] |
|||
Imagem:Carl Friedrich Gauss.jpg|[[Carl Friedrich Gauss|Gauss]] |
|||
Imagem:1925 kurt gödel.png|[[Kurt Gödel|Gödel]] |
|||
Imagem:William Rowan Hamilton painting.jpg|[[William Rowan Hamilton|Hamilton]] |
|||
Imagem:Hilbert.jpg|[[David Hilbert|Hilbert]] |
|||
Imagem:Carl Jacobi2.jpg|[[Carl Gustav Jakob Jacobi|Jacobi]] |
|||
Imagem:033-Earth-could-not-answer-nor-the-Seas-that-mourn-q75-829x1159.jpg|[[Omar Khayyām|Khayyām]] |
|||
Imagem:Felix Christian Klein.jpg|[[Felix Klein|Klein]] |
|||
Imagem:Andrej Nikolajewitsch Kolmogorov.jpg|[[Andrei Kolmogorov|Kolmogorov]] |
|||
Imagem:Lagrange_portrait.jpg|[[Joseph-Louis de Lagrange|Lagrange]] |
|||
Imagem:Pierre-Simon Laplace.jpg|[[Pierre Simon Laplace|Laplace]] |
|||
Imagem:Gottfried Wilhelm Leibniz, Bernhard Christoph Francke.jpg|[[Gottfried Wilhelm Leibniz|Leibniz]] |
|||
Imagem:Lebesgue 2.jpeg|[[Henri Lebesgue|Lebesgue]] |
|||
Imagem:Lobachevsky.jpg|[[Nikolai Lobachevsky|Lobachevsky]] |
|||
Imagem:John Forbes Nash, Jr. by Peter Badge.jpg|[[John Forbes Nash|Nash]] |
|||
Imagem:JohnvonNeumann-LosAlamos.jpg|[[John von Neumann|Neumann]] |
|||
Imagem:Sir_Isaac_Newton_(1643-1727).jpg|[[Sir Isaac Newton|Newton]] |
|||
Imagem:Noether.jpg|[[Emmy Noether|Noether]] |
|||
Imagem:Blaise Pascal 2.jpg|[[Blaise Pascal|Pascal]] |
|||
Imagem:Giuseppe Peano.jpg|[[Giuseppe Peano|Peano]] |
|||
Imagem:Kapitolinischer Pythagoras.jpg|[[Pitágoras]] |
|||
Imagem:JH Poincare.jpg|[[Henri Poincaré|Poincaré]] |
|||
Imagem:Lev Pontrjagin.jpg|[[Lev Pontryagin|Pontryagin]] |
|||
Imagem:Srinivasa Ramanujan - OPC - 1.jpg|[[Srinivasa Ramanujan|Ramanujan]] |
|||
Imagem:Riemann.jpg|[[Bernhard Riemann|Riemann]] |
|||
Imagem:JakobSteiner.jpg|[[Jakob Steiner|Steiner]] |
|||
Imagem:Karl Weierstrass 2.jpg|[[Karl Weierstrass|Weierstrass]] |
|||
Imagem:Hermann Weyl ETH-Bib Portr 00890.jpg|[[Hermann Weyl|Weyl]] |
|||
Imagem:Norbert wiener.jpg|[[Norbert Wiener|Wiener]] |
|||
Imagem:Ernst Zermelo 1900s.jpg|[[Ernst Zermelo|Zermelo]] |
|||
</gallery> |
|||
Atualmente, ainda há um debate [[Filosofia da matemática|filosófico]] sobre se a matemática pode ser classificada como uma ciência. No entanto, na prática, os matemáticos são normalmente considerados cientistas e a matemática tem muito em comum com as [[ciências físicas]], já que é [[Falseabilidade|falsificável]] como elas, o que significa em que, se um resultado ou uma teoria estiverem errados, isto pode ser provado por meio da apresentação de um [[contraexemplo]]. Da mesma forma que na ciência, as [[Teoria|teorias]] e os resultados matemáticos (teoremas) são frequentemente obtidos a partir da [[experimentação]],<ref>{{Citar web|url=https://undsci.berkeley.edu/article/mathematics|titulo=The science checklist applied: Mathematics|acessodata=27 de outubro de 2019|website=Understanding Science|publicado=[[Universidade da Califórnia em Berkeley]]|arquivourl=https://web.archive.org/web/20191027021023/https://undsci.berkeley.edu/article/mathematics|arquivodata=27 de outubro de 2019|urlmorta=live}}</ref> que pode consistir na computação de exemplos selecionados ou no estudo de figuras ou de outras representações de objetos matemáticos (muitas vezes representações mentais sem suporte físico). Por exemplo, quando questionado sobre como conseguiu seus teoremas, [[Gauss]] certa vez respondeu "durch planmässiges Tattonieren" ("através de experimentação sistemática").<ref>{{Citar livro|url={{GBurl|id=KwESE88CGa8C|q=durch planmässiges Tattonieren}}|título=Dictionary of Scientific Quotations|ultimo=Mackay|primeiro=A. L.|editora=Taylor & Francis|ano=1991|localização=Londres|isbn=978-0-7503-0106-0|acessodata=19 de março de 2023}}</ref> Contudo, alguns autores enfatizam que a matemática difere da noção moderna de ciência por não se basear em evidências [[Empirismo|empíricas]].<ref name="Bishop1991">{{Citar livro|título=Mathematical Enculturation: A Cultural Perspective on Mathematics Education|ultimo=Bishop|primeiro=Alan|editora=Kluwer Academic Publishers|ano=1991|localização=Norwell, Massachusetts|páginas=20–59|capitulo=Environmental activities and mathematical culture|isbn=978-0-7923-1270-3|acessodata=5 de abril de 2020}}</ref><ref>{{Citar livro|título=Out of Their Minds: The Lives and Discoveries of 15 Great Computer Scientists|ultimo=Shasha|primeiro=Dennis Elliot|ultimo2=Lazere|primeiro2=Cathy A.|editora=Springer|ano=1998|isbn=978-0-387-98269-4}}</ref><ref name="Nickles2013">{{Citar livro|título=Philosophy of Pseudoscience: Reconsidering the Demarcation Problem|ultimo=Nickles|primeiro=Thomas|editora=The University of Chicago Press|ano=2013|localização=Chicago|capitulo=The Problem of Demarcation|isbn=978-0-226-05182-6}}</ref><ref name="Pigliucci2014">{{Citar revista|sobrenome=Pigliucci|primeiro=Massimo|autorlink=Massimo Pigliucci|ano=2014|título=Are There 'Other' Ways of Knowing?|url=https://philosophynow.org/issues/102/Are_There_Other_Ways_of_Knowing|urlmorta=live|revista=Philosophy Now|arquivourl=https://web.archive.org/web/20200513190522/https://philosophynow.org/issues/102/Are_There_Other_Ways_of_Knowing|arquivodata=13 de maio de 2020|acessodata=6 de abril de 2020}}</ref> |
|||
== Ver também == |
|||
{{correlatos |
|||
=== Matemática pura e aplicada === |
|||
|commons=Mathematics |
|||
| |
{{AP|Matemática pura|Matemática aplicada}} |
||
{{multiple image |
|||
|wikilivros=Matemática |
|||
| footer = [[Isaac Newton]] (esquerda) and [[Gottfried Wilhelm Leibniz]] desenvolveram o [[cálculo infinitesimal]] |
|||
|wikcionario=Matemática |
|||
| total_width = 330 |
|||
|wikiversidade=Portal:Matemática e Estatística |
|||
| width1 = 407 |
|||
|wikinotícias=matemática |
|||
| height1 = 559 |
|||
| image1 = GodfreyKneller-IsaacNewton-1689.jpg |
|||
| alt1 = Isaac Newton |
|||
| width2 = 320 |
|||
| height2 = 390 |
|||
| image2 = Gottfried Wilhelm Leibniz, Bernhard Christoph Francke.jpg |
|||
| alt2 = Gottfried Wilhelm von Leibniz |
|||
}} |
}} |
||
Até ao século XIX, o desenvolvimento da matemática no [[mundo ocidental]] era motivado principalmente pelas necessidades trazidas pela [[tecnologia]] e ciência, sendo que não havia uma distinção clara entre [[matemática pura]] e [[Matemática aplicada|aplicada]].<ref name="Ferreirós_2007">{{Citar livro|título=The Shaping of Arithmetic after C.F. Gauss's Disquisitiones Arithmeticae|ultimo=Ferreirós|primeiro=J.|editora=Springer Science & Business Media|ano=2007|editor=Catherine Goldstein|páginas=235–268|capitulo=Ό Θεὸς Άριθμητίζει: The Rise of Pure Mathematics as Arithmetic with Gauss|isbn=978-3-540-34720-0}}</ref> Por exemplo, os [[números naturais]] e a aritmética foram introduzidos pela necessidade de [[Contagem (matemática)|contagem]], enquanto a geometria foi motivada pela [[topografia]], [[arquitetura]] e [[astronomia]]. Mais tarde, Isaac Newton introduziu o conceito do [[cálculo infinitesimal]] para explicar o movimento dos [[Planeta|planetas]] com sua [[lei da gravitação universal]]. Além disso, a maioria dos matemáticos eram cientistas e muitos cientistas também eram matemáticos.<ref>{{Citar periódico |título=Mathematical vs. Experimental Traditions in the Development of Physical Science |periódico=The Journal of Interdisciplinary History |publicado=The MIT Press |número=1 |ultimo=Kuhn |primeiro=Thomas S. |autorlink=Thomas Kuhn |ano=1976 |paginas=1–31 |doi=10.2307/202372 |jstor=202372 |volume=7}}</ref> Contudo, uma exceção notável ocorreu com a tradição da matemática pura na [[Grécia Antiga]].<ref>{{Citar livro|título=The Oxford Handbook of the History of Mathematics|ultimo=Asper|primeiro=Markus|editora=OUP Oxford|ano=2009|editor-sobrenome=Robson|series=Oxford Handbooks in Mathematics|páginas=107–132|capitulo=The two cultures of mathematics in ancient Greece|isbn=978-0-19-921312-2|acessodata=18 de novembro de 2022|editor-sobrenome2=Stedall}}</ref> O problema da [[fatoração de inteiros]], por exemplo, que remonta a [[Euclides]] em 300 a.C., não tinha aplicação prática antes de seu uso no [[RSA (sistema criptográfico)|criptossistema RSA]], que atualmente é amplamente utilizado para a segurança de [[Rede de computadores|redes de computadores]].<ref>{{Citar livro|título=Emerging Security Algorithms and Techniques|ultimo=Gozwami|primeiro=Pinkimani|ultimo2=Singh|primeiro2=Madan Mohan|editora=CRC Press|ano=2019|editor-sobrenome=Ahmad|páginas=59–60|capitulo=Integer Factorization Problem|isbn=978-0-8153-6145-9|lccn=2019010556|oclc=1082226900|editor-sobrenome2=Doja|editor-nome2=M. N.|editor-sobrenome3=Udzir|editor-nome3=Nur Izura|editor-sobrenome4=Singh|editor-nome4=Manu Pratap}}</ref> No século XIX, matemáticos como os alemães [[Karl Weierstrass]] e [[Richard Dedekind]] concentraram cada vez mais as suas pesquisas em problemas internos, ou seja, na chamada ''matemática pura''.<ref name="Ferreirós_2007" /><ref>{{Citar periódico |url=http://pgrim.org/philosophersannual/pa28articles/maddyhowapplied.pdf |título=How applied mathematics became pure |acessodata=19 de novembro de 2022 |periódico=The Review of Symbolic Logic |número=1 |ultimo=Maddy |primeiro=P. |autorlink=Penelope Maddy |ano=2008 |paginas=16–41 |doi=10.1017/S1755020308080027 |arquivourl=https://web.archive.org/web/20170812012210/http://pgrim.org/philosophersannual/pa28articles/maddyhowapplied.pdf |arquivodata=12 de agosto de 2017 |volume=1}}</ref> Isto levou à divisão da matemática em matemáticas ''pura'' e ''aplicada'', sendo a última geralmente considerada de menor valor entre os puristas matemáticos. No entanto, a linha que diferencia as duas é tênue.<ref>{{Citar livro|título=The Best Writing on Mathematics, 2016|ultimo=Silver|primeiro=Daniel S.|editora=Princeton University Press|ano=2017|editor-sobrenome=Pitici|páginas=17–26|capitulo=In Defense of Pure Mathematics|isbn=978-0-691-17529-4|acessodata=19 de novembro de 2022}}</ref> |
|||
* '''Áreas da matemática''' |
|||
** [[Aritmética]] |
|||
** [[Álgebra]] |
|||
*** [[Álgebra booleana]] |
|||
** [[Geometria]] |
|||
** [[Geometria analítica]] |
|||
** [[Trigonometria]] |
|||
** [[Porcentagem]] |
|||
** [[Estatística]] |
|||
** [[História da matemática]] |
|||
* Disciplinas que evoluíram a partir da matemática: |
|||
** [[Informática]] |
|||
* [[Educação matemática]] |
|||
* [[Problemas em aberto da Matemática]] |
|||
* Olimpíadas |
|||
** [[Olimpíada Internacional de Matemática]] |
|||
** [[Olimpíada Brasileira de Matemática]] |
|||
** [[Olimpíadas Portuguesas de Matemática]] |
|||
** [[Olimpíada Brasileira de Matemática das Escolas Públicas]] |
|||
* Prémios |
|||
** [[Prémio Abel]] |
|||
** [[Prémios Clay|Prémio Problemas do Milênio]] (Clay Math Prize) |
|||
** [[Medalha Fields]] |
|||
** [[Competições matemáticas]] |
|||
* Softwares |
|||
** Proprietários: |
|||
*** [[Derive]] |
|||
*** [[Maple]] |
|||
*** [[Mathematica]] |
|||
*** [[Matlab]] |
|||
** Livres: |
|||
*** [[Maxima]] |
|||
*** [[Octave]] |
|||
*** [[Scilab]] |
|||
*** [[Scipy]] |
|||
*** [[Geogebra]] |
|||
* [[Beleza da matemática]] |
|||
As consequências da [[Segunda Guerra Mundial]] levou a um aumento no desenvolvimento da matemática aplicada nos Estados Unidos e em outros lugares.<ref>{{Citar periódico |url=https://www.ams.org/journals/bull/2022-59-03/S0273-0979-2022-01754-5/home.html |título=The American Mathematical Society and Applied Mathematics from the 1920s to the 1950s: A Revisionist Account |acessodata=20 de novembro de 2022 |periódico=Bulletin of the American Mathematical Society |número=3 |ultimo=Parshall |primeiro=Karen Hunger |autorlink=Karen Hunger Parshall |ano=2022 |paginas=405–427 |doi=10.1090/bull/1754 |arquivourl=https://web.archive.org/web/20221120151259/https://www.ams.org/journals/bull/2022-59-03/S0273-0979-2022-01754-5/home.html |arquivodata=20 de novembro de 2022 |volume=59 |doi-access=free}}</ref><ref>{{Citar periódico |url=https://www.researchgate.net/publication/226795930 |título=The History Of Applied Mathematics And The History Of Society |acessodata=20 de novembro de 2022 |periódico=Synthese |ultimo=Stolz |primeiro=Michael |ano=2002 |paginas=43–57 |doi=10.1023/A:1020823608217 |volume=133}}</ref> Muitas das teorias desenvolvidas para aplicações foram consideradas interessantes do ponto de vista da matemática pura e muitos resultados da matemática pura demonstraram ter aplicações fora da matemática; por sua vez, o estudo destas aplicações poderá fornecer novos desenvolvimentos sobre a “teoria pura”.<ref>{{Citar periódico |título=On the role of applied mathematics |data=Março de 1976 |periódico=[[Advances in Mathematics]] |número=3 |ultimo=Lin |primeiro=C. C . |paginas=267–288 |doi=10.1016/0001-8708(76)90024-4 |volume=19 |doi-access=free}}</ref><ref>{{Citar conferência |ultimo=Peressini |primeiro=Anthony |url=https://www.academia.edu/download/32799272/ApplyingMathPSA.pdf |titulo=Applying Pure Mathematics |data=Setembro de 1999 |acessodata=30 de novembro de 2022 |paginas=S1–S13 |conferencia=Philosophy of Science. Proceedings of the 1998 Biennial Meetings of the Philosophy of Science Association. Part I: Contributed Papers |jstor=188757 |arquivourl=https://web.archive.org/web/20240102210931/https://d1wqtxts1xzle7.cloudfront.net/32799272/ApplyingMathPSA-libre.pdf?1391205742=&response-content-disposition=inline%3B+filename%3DApplying_Pure_Mathematics.pdf&Expires=1704233371&Signature=BvNJyYufdj9BiKFe94w6gdXLpAfr7T5JIv~RU74R2uT0O9Ngj6i4cdBtYYOSB6D4V-MgButb6lKNhIGGQogw0e0sHVFkJUy5TRsoCiQ-MLabpZOf74E5SGLMFIExhGVAw7SKrSFaQsFGhfbaRMxbMP~u-wRdJAz6ve6kbWr6oq-doQeEOlRfO4EByNCUYx-KAk3~cBsH1Q2WNZ5QiVObMI1ufQ7zkQM1bqzOumLu6g07F~pt~Cds~lftuQufHomoTH-V9H9iKQgUyc3-4bEB1y1Jdngs7WWg76LcSGn65bPK8dxvsZzKaLDGfoK5jamZkA8z3-xxiMIPL8c6YETjZA__&Key-Pair-Id=APKAJLOHF5GGSLRBV4ZA |arquivodata=2 de janeiro de 2024 |volume=66}}</ref> Um exemplo do primeiro caso é a [[teoria das distribuições]], introduzida por [[Laurent Schwartz]] para validar cálculos feitos em [[mecânica quântica]], que se tornou imediatamente uma importante ferramenta de análise matemática (pura).<ref>{{Citar conferência |ultimo=Lützen |primeiro=J. |titulo=Mathematics meets physics: A contribution to their interaction in the 19th and the first half of the 20th century |acessodata=19 de novembro de 2022 |publicado=Verlag Harri Deutsch |ano=2011 |arquivourl=https://web.archive.org/web/20230323164143/https://slub.qucosa.de/api/qucosa%3A16267/zip/|url=https://slub.qucosa.de/api/qucosa%3A16267/zip/ |arquivodata=23 de março de 2023}}</ref> Um exemplo do segundo caso é a decidibilidade da teoria de primeira ordem dos números reais, um problema de matemática pura que foi provado verdadeiro por [[Alfred Tarski]], com um algoritmo impossível de [[Implementação de software|implementar]] devido a uma complexidade computacional bastante elevada.<ref>{{Citar periódico |url=https://www.ams.org/notices/199607/ |título=Model theory and exponentiation |data=Julho de 1996 |acessodata=19 de novembro de 2022 |periódico=Notices of the American Mathematical Society |número=7 |ultimo=Marker |primeiro=Dave |paginas=753–759 |arquivourl=https://web.archive.org/web/20140313004011/http://www.ams.org/notices/199607/ |arquivodata=13 de março de 2014 |volume=43}}</ref> Para obter um algoritmo que possa ser implementado e possa resolver sistemas de equações e desigualdades polinomiais, o matemática estadunidense George Collins introduziu a decomposição algébrica cilíndrica que se tornou uma ferramenta fundamental na geometria algébrica real.<ref>{{Citar conferência |ultimo=Chen |primeiro=Changbo |ultimo2=Maza |primeiro2=Marc Moreno |url=https://www.researchgate.net/publication/268067322 |titulo=Cylindrical Algebraic Decomposition in the RegularChains Library |data=agosto de 2014 |acessodata=19 de novembro de 2022 |publicado=Springer |series=Lecture Notes in Computer Science |conferencia=International Congress on Mathematical Software 2014 |doi=10.1007/978-3-662-44199-2_65 |volume=8592}}</ref> Nos dias atuais, a distinção entre matemática pura e aplicada é mais uma questão de objetivo de pesquisa do que uma divisão da matemática em áreas amplas.<ref>{{Citar periódico |título=Purifying applied mathematics and applying pure mathematics: how a late Wittgensteinian perspective sheds light onto the dichotomy |periódico=European Journal for Philosophy of Science |número=1 |ultimo=Pérez-Escobar |primeiro=José Antonio |ultimo2=Sarikaya |primeiro2=Deniz |ano=2021 |paginas=1–22 |doi=10.1007/s13194-021-00435-9 |volume=12 |doi-access=free}}</ref><ref>{{Citar livro|título=A Mathematical Approach to Research Problems of Science and Technology|ultimo=Takase|primeiro=M.|editora=Springer|ano=2014|series=Mathematics for Industry|volume=5|páginas=393–399|capitulo=Pure Mathematics and Applied Mathematics are Inseparably Intertwined: Observation of the Early Analysis of the Infinity|doi=10.1007/978-4-431-55060-0_29|isbn=978-4-431-55059-4|acessodata=20 de novembro de 2022|local-publicação=Tokyo}}</ref> A Classificação de Disciplinas de Matemática, por exemplo, tem uma seção para "matemática geral aplicada", mas não menciona "matemática pura".<ref name="MSC">{{Citar web|url=https://zbmath.org/static/msc2020.pdf|titulo=MSC2020-Mathematics Subject Classification System|acessodata=3 de fevereiro de 2024|website=zbMath|publicado=Associate Editors of Mathematical Reviews and zbMATH|arquivourl=https://web.archive.org/web/20240102023805/https://zbmath.org/static/msc2020.pdf|arquivodata=2 de janeiro de 2024|urlmorta=live}}</ref> |
|||
{{Referências|col=2}} |
|||
=== Eficácia irracional === |
|||
== Bibliografia == |
|||
A eficácia irracional da matemática é um fenômeno que foi nomeado e explicitado pela primeira vez pelo físico [[Eugene Wigner]]<ref name="wigner1960"/> e descreve o fato de que muitas teorias matemáticas (mesmo as mais “puras”) têm aplicações fora do seu objeto inicial. Estas aplicações podem estar completamente fora da sua área inicial e podem dizer respeito a fenômenos físicos que eram completamente desconhecidos quando a teoria matemática foi introduzida.<ref>{{Citar periódico |título=Revisiting the 'unreasonable effectiveness' of mathematics |data=10 de fevereiro de 2005 |periódico=Current Science |número=3 |ultimo=Sarukkai |primeiro=Sundar |paginas=415–423 |jstor=24110208 |volume=88}}</ref> Um exemplo notável é a [[Fatoração de inteiros|fatoração primária]] de números naturais que foi descoberta mais de 2 mil anos antes de seu uso comum para comunicações seguras na [[Internet]] através do [[RSA (sistema criptográfico)|sistema criptográfico RSA]].<ref>{{Citar livro|título=Computational Cryptography, Algorithmic Aspects of Cryptography, A Tribute to AKL|ultimo=Wagstaff, Jr.|primeiro=Samuel S.|editora=Cambridge University Press|ano=2021|editor-sobrenome=Bos|series=London Mathematical Society Lecture Notes Series 469|páginas=41–77|capitulo=History of Integer Factoring|acessodata=20 de novembro de 2022|editor-sobrenome2=Stam|arquivourl=https://web.archive.org/web/20221120155733/https://www.cs.purdue.edu/homes/ssw/chapter3.pdf|url=https://www.cs.purdue.edu/homes/ssw/chapter3.pdf|arquivodata=20 de novembro de 2022}}</ref> Um segundo exemplo histórico é a teoria das [[Elipse|elipses]]. Elas foram estudadas pelos [[Matemática da Grécia Antiga|antigos matemáticos gregos]] como [[Cónica|seções cônicas]] (isto é, interseções de [[Cone|cones]] com planos). Quase 2 mil anos depois, [[Johannes Kepler]] descobriu que as [[Trajetória|trajetórias]] dos planetas são elipses.<ref>{{Citar web|url=https://mathshistory.st-andrews.ac.uk/Curves/Ellipse/|titulo=Curves: Ellipse|acessodata=20 de novembro de 2022|publicado=[[Universidade de St Andrews]]|arquivourl=https://web.archive.org/web/20221014051943/https://mathshistory.st-andrews.ac.uk/Curves/Ellipse/|arquivodata=14 de outubro de 2022|urlmorta=live}}</ref> |
|||
* BOYER, Carl B. ''História da matemática''. 2ª Edição. São Paulo: Edgard Blücher Ltda, 1996. ISBN 8521200234. |
|||
* COURANT, Richard; ROBBINS, Herbert. ''O que é Matemática?''. Ciência Moderna, 2000. ISBN 8573930217. |
|||
Durante o século XIX, o desenvolvimento interno da geometria (ou [[matemática pura]]) levou à definição e ao estudo de [[Geometria não euclidiana|geometrias não euclidianas]], espaços de dimensão superior a três e [[Variedade (matemática)|variedades]]. Neste período, estes conceitos pareciam totalmente desligados da realidade física. No início do século XX, no entanto, o alemão [[Albert Einstein]] desenvolveu a [[teoria da relatividade]] que utiliza fundamentalmente estes conceitos, principalmente o [[espaço-tempo]] da [[relatividade restrita]] é um espaço não euclidiano de dimensão quatro, enquanto o espaço-tempo da [[relatividade geral]] é uma variedade (curva) de dimensão quatro.<ref>{{Citar web|ultimo=Mukunth|primeiro=Vasudevan|url=https://thewire.in/science/beyond-the-surface-of-einsteins-relativity-lay-a-chimerical-geometry|titulo=Beyond the Surface of Einstein's Relativity Lay a Chimerical Geometry|data=10 de setembro de 2015|acessodata=20 de novembro de 2022|website=The Wire|arquivourl=https://web.archive.org/web/20221120191206/https://thewire.in/science/beyond-the-surface-of-einsteins-relativity-lay-a-chimerical-geometry|arquivodata=20 de novembro de 2022|urlmorta=live}}</ref><ref>{{Citar periódico |título=The Space-Time Manifold of Relativity. The Non-Euclidean Geometry of Mechanics and Electromagnetics |data=Novembro de 1912 |periódico=Proceedings of the American Academy of Arts and Sciences |número=11 |ultimo=Wilson |primeiro=Edwin B. |ultimo2=Lewis |primeiro2=Gilbert N. |paginas=389–507 |doi=10.2307/20022840 |jstor=20022840 |volume=48}}</ref> |
|||
* DEVLIN, Keith. ''Matemática: a Ciência dos Padrões''. Editora Porto, 2003. ISBN 9720451335. |
|||
Um aspecto marcante da interação entre matemática e física é quando a matemática impulsiona a pesquisa em física, o que é exemplificado pelas descobertas do [[pósitron]] e do [[Bárion omega|bárion]] <math>\Omega^{-}</math>. Em ambos os casos, as equações das teorias apresentavam soluções inexplicáveis, o que levou à conjectura da existência de uma [[partícula]] desconhecida. Em ambos os casos, estas partículas foram descobertas alguns anos depois através de experiências específicas.<ref name="borel">{{Citar periódico |título=Mathematics: Art and Science |periódico=The Mathematical Intelligencer |publicado=Springer |número=4 |ultimo=Borel |primeiro=Armand |autorlink=Armand Borel |ano=1983 |paginas=9–17 |doi=10.4171/news/103/8 |issn=1027-488X |volume=5 |doi-access=free}}</ref><ref>{{Citar periódico |título=Discovering the Positron (I) |data=novembro de 1961 |periódico=The British Journal for the Philosophy of Science |publicado=The University of Chicago Press |número=47 |ultimo=Hanson |primeiro=Norwood Russell |autorlink=Norwood Russell Hanson |paginas=194–214 |doi=10.1093/bjps/xiii.49.54 |jstor=685207 |volume=12}}</ref><ref>{{Citar periódico |título=Avoiding reification: Heuristic effectiveness of mathematics and the prediction of the Ω<sup>–</sup> particle |data=Fevereiro de 2016 |periódico=Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics |ultimo=Ginammi |primeiro=Michele |paginas=20–27 |bibcode=2016SHPMP..53...20G |doi=10.1016/j.shpsb.2015.12.001 |volume=53}}</ref> |
|||
=== Ciências específicas === |
|||
==== Física ==== |
|||
{{AP|Relação entre matemática e física}} |
|||
[[Ficheiro:Pendule_schema.gif|miniaturadaimagem|Diagrama de um [[pêndulo]]]] |
|||
A matemática e a física influenciaram-se mutuamente ao longo da história moderna. A [[física moderna]] utliza amplamente a matemática<ref>{{Citar livro|url={{GBurl|id=-DmfVjBUPksC|p=3}}|título=Essentials of Physics|ultimo=Wagh|primeiro=Sanjay Moreshwar|ultimo2=Deshpande|primeiro2=Dilip Abasaheb|data=27 de setembro de 2012|editora=PHI Learning Pvt. Ltd.|língua=en|isbn=978-81-203-4642-0|acessodata=3 de janeiro de 2023}}</ref> e é também a motivação por trás de grandes desenvolvimentos na matemática.<ref>{{Citar conferência |ultimo=Atiyah |primeiro=Michael |autorlink=Michael Atiyah |url=http://www.mathunion.org/ICM/ICM1990.1/Main/icm1990.1.0031.0036.ocr.pdf |titulo=On the Work of Edward Witten |data=1990 |acessodata=29 de dezembro de 2022 |pagina=31 |conferencia=Proceedings of the International Congress of Mathematicians |arquivourl=https://web.archive.org/web/20130928095313/http://www.mathunion.org/ICM/ICM1990.1/Main/icm1990.1.0031.0036.ocr.pdf |arquivodata=28 de setembro de 2013}}</ref> |
|||
==== Informática ==== |
|||
{{AP|Informática}} |
|||
A ascensão da [[tecnologia]] no século XX abriu caminho para uma nova ciência: a [[computação]].{{Nre|[[Ada Lovelace]] é conhecida por ter escrito, na década de 1840, o primeiro programa de computador em colaboração com [[Charles Babbage]]}} Este campo está intimamente relacionado à matemática de várias maneiras. A [[ciência da computação teórica]], por exemplo, é essencialmente de natureza matemática. Em contrapartida, a [[informática]] também se tornou essencial para a obtenção de novos resultados. Este é um grupo de técnicas conhecidas como [[matemática experimental]].<ref>{{Citar web|ultimo=Borwein|primeiro=J.|ultimo2=Borwein|primeiro2=P.|url=http://oldweb.cecm.sfu.ca/organics/vault/expmath/expmath/html/node16.html|titulo=Conclusion|data=1996|website=oldweb.cecm.sfu.ca|arquivourl=https://web.archive.org/web/20080121081424/http://oldweb.cecm.sfu.ca/organics/vault/expmath/expmath/html/node16.html|arquivodata=21 de janeiro de 2008|urlmorta=dead|ultimo3=Girgensohn|primeiro3=R.|ultimo4=Parnes|primeiro4=S.}}</ref> O exemplo mais conhecido é o [[teorema das quatro cores]], comprovado em 1976 com a ajuda de um [[computador]]. Isto revolucionou a matemática tradicional, onde a regra até então era que o matemático verificasse cada parte da prova. Em 1998, a [[conjectura de Kepler]] sobre [[empacotamento de esferas]] também parecia ter sido parcialmente comprovada por um computador. Desde então, uma equipe internacional trabalhou na redação de uma prova formal, que foi concluída (e verificada) em 2015.<ref>{{Citar periódico |url=https://www.cambridge.org/core/journals/forum-of-mathematics-pi/article/formal-proof-of-the-kepler-conjecture/78FBD5E1A3D1BCCB8E0D5B0C463C9FBC |título=A Formal Proof of the Kepler Conjecture |data=2017 |acessodata=25 de fevereiro de 2023 |periódico=Forum of Mathematics, Pi |ultimo=Hales |primeiro=Thomas |ultimo2=Adams |primeiro2=Mark |pagina=e2 |lingua=en |doi=10.1017/fmp.2017.1 |issn=2050-5086 |arquivourl=https://web.archive.org/web/20201204053232/https://www.cambridge.org/core/journals/forum-of-mathematics-pi/article/formal-proof-of-the-kepler-conjecture/78FBD5E1A3D1BCCB8E0D5B0C463C9FBC |arquivodata=4 de dezembro de 2020 |ultimo3=Bauer |primeiro3=Gertrud |ultimo4=Dang |primeiro4=Tat Dat |ultimo5=Harrison |primeiro5=John |ultimo6=Hoang |primeiro6=Le Truong |ultimo7=Kaliszyk |primeiro7=Cezary |ultimo8=Magron |primeiro8=Victor |ultimo9=Mclaughlin |primeiro9=Sean |volume=5}}</ref> Um grande problema em aberto na ciência da computação teórica é [[P versus NP]], um dos sete [[Problemas do Prêmio Millennium]].<ref>{{Citar web|url=https://www.britannica.com/science/P-versus-NP-problem|titulo=P versus NP problem {{!}} mathematics|acessodata=29 de dezembro de 2022|website=Britannica|lingua=en|arquivourl=https://web.archive.org/web/20221206044556/https://www.britannica.com/science/P-versus-NP-problem|arquivodata=6 de dezembro de 2022|urlmorta=live}}</ref> |
|||
==== Biologia ==== |
|||
{{AP|Biologia matemática e teórica}} |
|||
[[Ficheiro:Giant_Pufferfish_skin_pattern_detail.jpg|miniaturadaimagem|A pele deste [[Baiacu-gigante|baiacu gigante]] exibe um [[padrão de Turing]], que pode ser modelado por [[Modelo de reação-difusão|sistemas de reação-difusão]]]] |
|||
A [[biologia]] utiliza extensivamente a [[probabilidade]], como por exemplo na [[ecologia]] ou na [[Neurociência|neurobiologia]].<ref name=":2">{{Citar livro|título=The Oxford Handbook of Probability and Philosophy|ultimo=Millstein|primeiro=Roberta|data=8 de setembro de 2016|editor-sobrenome=Hájek|editor-nome=Alan|páginas=601–622|capitulo=Probability in Biology: The Case of Fitness|doi=10.1093/oxfordhb/9780199607617.013.27|acessodata=29 de dezembro de 2022|editor-sobrenome2=Hitchcock|editor-nome2=Christopher|arquivourl=https://web.archive.org/web/20230307054456/http://philsci-archive.pitt.edu/10901/1/Millstein-fitness-v2.pdf|url=http://philsci-archive.pitt.edu/10901/1/Millstein-fitness-v2.pdf|arquivodata=7 de março de 2023}}</ref> A maior parte do debate sobre probabilidade em biologia, entretanto, centra-se no conceito de [[Aptidão|aptidão evolutiva]].<ref name=":2" /> |
|||
A ecologia usa amplamente a [[Modelagem matemática|modelagem]] para simular a [[dinâmica populacional]],<ref name=":2"/><ref>See for example Anne Laurent, Roland Gamet, Jérôme Pantel, ''Tendances nouvelles en modélisation pour l'environnement, actes du congrès «Programme environnement, vie et sociétés»'' 15-17 janvier 1996, CNRS</ref> estudar [[ecossistemas]] como o modelo predador-presa, medir a difusão da [[poluição]],{{Sfn|Bouleau|1999|pp=282–283}} ou para avaliar as [[mudanças climáticas]].{{Sfn|Bouleau|1999|p=285}} A dinâmica de uma população pode ser modelada por equações diferenciais acopladas, como as [[Equação de Lotka-Volterra|equações de Lotka-Volterra]].<ref>{{Citar web|url=https://math.libretexts.org/Bookshelves/Applied_Mathematics/Mathematical_Biology_(Chasnov)/01%3A_Population_Dynamics/1.04%3A_The_Lotka-Volterra_Predator-Prey_Model|titulo=1.4: The Lotka-Volterra Predator-Prey Model|data=5 de janeiro de 2022|acessodata=29 de dezembro de 2022|website=Mathematics LibreTexts|lingua=en|arquivourl=https://web.archive.org/web/20221229204111/https://math.libretexts.org/Bookshelves/Applied_Mathematics/Mathematical_Biology_(Chasnov)/01:_Population_Dynamics/1.04:_The_Lotka-Volterra_Predator-Prey_Model|arquivodata=29 de dezembro de 2022|urlmorta=live}}</ref> No entanto, existe o problema da [[validação do modelo]]. Isto é particularmente grave quando os resultados da modelização influenciam as decisões políticas; a existência de modelos contraditórios poderia permitir às nações escolher o modelo mais favorável.{{Sfn|Bouleau|1999|p=287}} |
|||
==== Ciências sociais ==== |
|||
{{AP|Ciências sociais}} |
|||
As áreas da matemática utilizadas nas [[ciências sociais]] incluem [[probabilidade]]/[[estatística]] e [[equações diferenciais]], que são usadas em [[linguística]], [[economia]], [[sociologia]]<ref>{{Citar periódico |url=https://www.annualreviews.org/doi/10.1146/annurev.soc.28.110601.140942 |título=Mathematics in Sociology |data=2002 |periódico=Annual Review of Sociology |número=1 |ultimo=Edling |primeiro=Christofer R. |paginas=197–220 |lingua=en |doi=10.1146/annurev.soc.28.110601.140942 |issn=0360-0572 |volume=28}}</ref> e [[psicologia]].<ref>{{Citation|last=Batchelder|first1=William H.|title=Mathematical Psychology: History|date=2015-01-01|url=https://www.sciencedirect.com/science/article/pii/B978008097086843059X|pages=808–815|editor-last=Wright|editor-first=James D.|access-date=2023-09-30|place=Oxford|publisher=Elsevier|isbn=978-0-08-097087-5}}</ref> |
|||
[[Ficheiro:Supply-demand-equilibrium.svg|miniaturadaimagem| [[Lei da oferta e da procura|Curvas de oferta e demanda]], como esta, são um elemento básico da economia matemática.]] |
|||
O postulado fundamental da [[economia matemática]] é o do ator individual racional – ''[[Homo economicus]]'' ({{Tradução literal|homem econômico}}).<ref name=":3">{{Citar livro|url={{GBurl|id=6QrvmNo2qD4C|p=158}}|título=Moral Markets: The Critical Role of Values in the Economy|ultimo=Zak|primeiro=Paul J.|data=2010|editora=Princeton University Press|língua=en|isbn=978-1-4008-3736-6|acessodata=3 de janeiro de 2023}}</ref> Neste modelo, o indivíduo busca maximizar seu [[Teoria da escolha racional|interesse próprio]]<ref name=":3" /> e sempre faz escolhas ótimas usando [[Informação perfeita|informações perfeitas]].<ref name=":4">{{Citar web|ultimo=Kim|primeiro=Oliver W.|url=https://www.thecrimson.com/column/homo-economicus/article/2014/9/19/Harvard-homo-economicus-fiction/|titulo=Meet Homo Economicus|data=29 de maio de 2014|acessodata=29 de dezembro de 2022|website=The Harvard Crimson|arquivourl=https://web.archive.org/web/20221229204106/https://www.thecrimson.com/column/homo-economicus/article/2014/9/19/Harvard-homo-economicus-fiction/|arquivodata=29 de dezembro de 2022|urlmorta=live}}</ref> Contudo, muitas pessoas rejeitaram ou criticaram o conceito.<ref name=":4" /> Economistas observam que pessoas reais têm informações limitadas, fazem escolhas erradas e se preocupam com a justiça, o altruísmo e não apenas com o ganho pessoal.<ref name=":4" /> |
|||
No início do século XX, houve um desenvolvimento no sentido de expressar movimentos históricos através de fórmulas. Por exemplo, em 1922, [[Nikolai Kondratiev]] discerniu o [[Ondas de Kondratiev|ciclo Kondratiev]] de aproximadamente 50 anos, que explica fases de crescimento ou de [[crise econômica]].<ref>{{Citar web|url=https://www.encyclopedia.com/history/encyclopedias-almanacs-transcripts-and-maps/kondratiev-nikolai-dmitrievich|titulo=Kondratiev, Nikolai Dmitrievich {{!}} Encyclopedia.com|acessodata=29 de dezembro de 2022|website=www.encyclopedia.com|arquivourl=https://web.archive.org/web/20160701224009/http://www.encyclopedia.com/doc/1G2-3404100667.html|arquivodata=1 de julho de 2016|urlmorta=live}}</ref> No final do século XIX, Nicolas-Remi Brück e Charles Henri Lagrange estenderam suas análises à [[geopolítica]].<ref>{{Citar web|url=https://onlinebooks.library.upenn.edu/webbin/book/lookupid?key=ha010090244#:~:text=##+Math%C3%A9matique+de+l'histoire,org%E3%80%91|titulo=Mathématique de l'histoire-géometrie et cinématique. Lois de Brück. Chronologie géodésique de la Bible., by Charles LAGRANGE et al. | The Online Books Page|website=onlinebooks.library.upenn.edu}}</ref> Desde a década de 1990, o [[Antropologia evolucionária|antropólogo evolucionário]] russo-americano,[[Peter Turchin]] trabalha no desenvolvimento da [[cliodinâmica]].<ref>{{Citar web|url=https://www.zdnet.com/article/cliodynamics-a-science-for-predicting-the-future/|titulo=Cliodynamics: a science for predicting the future|acessodata=29 de dezembro de 2022|website=ZDNET|lingua=en|arquivourl=https://web.archive.org/web/20221229204104/https://www.zdnet.com/article/cliodynamics-a-science-for-predicting-the-future/|arquivodata=29 de dezembro de 2022|urlmorta=live}}</ref> |
|||
Mesmo assim, a matematização das ciências sociais não é isenta de perigos. No polêmico livro ''[[Imposturas Intelectuais]]'' (1997), [[Alan Sokal|Sokal]] e [[Jean Bricmont|Bricmont]] denunciaram o uso infundado ou abusivo de terminologia científica, especialmente da matemática ou da física, nas ciências sociais.<ref>{{Citar livro|url=https://archive.org/details/fashionablenonse00soka|título=Fashionable Nonsense|ultimo=Sokal|primeiro=Alan|ultimo2=Jean Bricmont|editora=Picador|ano=1998|localização=New York|isbn=978-0-312-19545-8|oclc=39605994|autorlink=Alan Sokal}}</ref> |
|||
== Relação com astrologia e esoterismo == |
|||
Alguns matemáticos renomados também foram considerados [[astrólogos]] renomados; por exemplo, [[Ptolemeu|Ptolomeu]], astrônomos árabes, [[Johannes Müller von Königsberg|Regiomontano]], [[Girolamo Cardano|Cardano]], [[Johannes Kepler|Kepler]], ou [[John Dee]]. Na [[Idade Média]], a [[astrologia]] era considerada uma ciência que incluía a matemática. Em sua enciclopédia, o físico suíço Theodor Zwinger escreveu que a astrologia era uma ciência matemática que estudava o "movimento ativo dos corpos à medida que agem sobre outros corpos" e reservou à matemática a necessidade de “calcular com probabilidade as influências [das estrelas]” para prever suas “conjunções e oposições”.<ref>{{Citar livro|url={{GBurl|id=92n7ZE8Iww8C|p=130}}|título=Comprendre et maîtriser la nature au Moyen Age: mélanges d'histoire des sciences offerts à Guy Beaujouan|ultimo=Beaujouan|primeiro=Guy|data=1994|editora=Librairie Droz|língua=fr|isbn=978-2-600-00040-6|acessodata=3 de janeiro de 2023}}</ref> Atualmente, no entanto, a astrologia não é mais considerada uma ciência, mas sim uma [[pseudociência]].<ref>{{Citar web|url=https://www.afis.org/L-astrologie-a-l-epreuve-ca-ne-marche-pas-ca-n-a-jamais-marche|titulo=L'astrologie à l'épreuve : ça ne marche pas, ça n'a jamais marché ! / Afis Science – Association française pour l'information scientifique|acessodata=28 de dezembro de 2022|website=Afis Science – Association française pour l’information scientifique|lingua=fr|arquivourl=https://web.archive.org/web/20230129204349/https://www.afis.org/L-astrologie-a-l-epreuve-ca-ne-marche-pas-ca-n-a-jamais-marche|arquivodata=29 de janeiro de 2023|urlmorta=live}}</ref> |
|||
== Filosofia == |
|||
{{AP|Filosofia da matemática}} |
|||
=== Realidade === |
|||
O matemático suíço [[Armand Borel]] resumiu esta visão da realidade matemática da seguinte forma, e forneceu citações de [[Godfrey Harold Hardy|G. H. Hardy]], [[Charles Hermite]], [[Henri Poincaré]] e [[Albert Einstein]] que apoiam seus pontos de vista.<ref name="borel">{{Citar periódico |título=Mathematics: Art and Science |periódico=The Mathematical Intelligencer |publicado=Springer |número=4 |ultimo=Borel |primeiro=Armand |autorlink=Armand Borel |ano=1983 |paginas=9–17 |doi=10.4171/news/103/8 |issn=1027-488X |volume=5 |doi-access=free}}</ref> Entretanto, o platonismo e as visões concorrentes sobre a abstração não explicam necessariamente a [[Matemática|eficácia irracional]] da matemática.<ref>{{Citar livro|título=The Software of the Universe, An Introduction to the History and Philosophy of Laws of Nature|ultimo=Dorato|primeiro=Mauro|editora=Ashgate|ano=2005|páginas=31–66|capitulo=Why are laws mathematical?|isbn=978-0-7546-3994-7|acessodata=5 de dezembro de 2022|arquivourl=https://web.archive.org/web/20230817111932/https://d1wqtxts1xzle7.cloudfront.net/52076815/2ch-libre.pdf?1488997736=&response-content-disposition=inline%3B+filename%3DChapter_2_of_the_book_the_software_of_th.pdf&Expires=1692274771&Signature=PXpNLBsmWMkz9YUs6~LUOfXNkmkCAmDfxQUoWOkGJKP4YqPGQUFMuP1I0xFycLZkL0dyfGwdGQ7mPk44nvmpM3YpKBSeVCZRXtDMiwgqs1JhEWrJovAhrchPLM1mGn3pw5P6LPo0sDZsl7uaPoZHMyCyJpayHvFtpyj1oUMIdmGuYM5P3euy1R87g6xlKyNAp~~BR5I4gVpopzLoeZn7d3oEnOOua0GjsqsZ6H9mEgcZMpH-qF8w9iFa9aSXFpqxagQwcVVkg7DXkOjVV5jyzctBUKQtOQQ~-9EN1y-c9pFV-Xu-NNuoN3Ij6K4SwvjYv0a8DMs8T5SVj1Kz9i4CEQ__&Key-Pair-Id=APKAJLOHF5GGSLRBV4ZA|url=https://d1wqtxts1xzle7.cloudfront.net/52076815/2ch-libre.pdf?1488997736=&response-content-disposition=inline%3B+filename%3DChapter_2_of_the_book_the_software_of_th.pdf&Expires=1692274771&Signature=PXpNLBsmWMkz9YUs6~LUOfXNkmkCAmDfxQUoWOkGJKP4YqPGQUFMuP1I0xFycLZkL0dyfGwdGQ7mPk44nvmpM3YpKBSeVCZRXtDMiwgqs1JhEWrJovAhrchPLM1mGn3pw5P6LPo0sDZsl7uaPoZHMyCyJpayHvFtpyj1oUMIdmGuYM5P3euy1R87g6xlKyNAp~~BR5I4gVpopzLoeZn7d3oEnOOua0GjsqsZ6H9mEgcZMpH-qF8w9iFa9aSXFpqxagQwcVVkg7DXkOjVV5jyzctBUKQtOQQ~-9EN1y-c9pFV-Xu-NNuoN3Ij6K4SwvjYv0a8DMs8T5SVj1Kz9i4CEQ__&Key-Pair-Id=APKAJLOHF5GGSLRBV4ZA|arquivodata=17 de agosto de 2023}}</ref> |
|||
=== Definições propostas === |
|||
Não existe um [[consenso]] geral sobre uma definição de matemática ou o seu [[Epistemologia|estatuto epistemológico]] {{Mdash}} isto é, o seu lugar entre outras atividades humanas.<ref name="Mura">{{Citar periódico |título=Images of Mathematics Held by University Teachers of Mathematical Sciences |data=Dezembro de 1993 |periódico=Educational Studies in Mathematics |número=4 |ultimo=Mura |primeiro=Roberta |paginas=375–85 |doi=10.1007/BF01273907 |jstor=3482762 |volume=25}}</ref><ref name="Runge">{{Citar livro|url={{GBurl|id=EDm0eQqFUQ4C|p=9}}|título=Iris Runge: A Life at the Crossroads of Mathematics, Science, and Industry|ultimo=Tobies|primeiro=Renate|ultimo2=Neunzert|primeiro2=Helmut|editora=Springer|ano=2012|isbn=978-3-0348-0229-1|acessodata=20 de junho de 2015}}</ref> Muitos matemáticos profissionais não têm interesse em uma definição ou consideram a matemática como algo indefinível.<ref name="Mura" /> Sequer há consenso sobre se a matemática pode ser considerada uma [[arte]] ou uma [[ciência]].<ref name="Runge" /> Alguns estudiosos apenas dizem que a “matemática é o que os matemáticos fazem”.<ref name="Mura" /> Isto faz sentido, pois existe um forte consenso entre eles sobre o que a matemática é e não é. A maioria das definições propostas tenta definir a matemática pelo seu objeto de estudo.<ref>{{Citar conferência |ultimo=Ziegler |primeiro=Günter M. |ultimo2=Loos |primeiro2=Andreas |titulo="What is Mathematics?" and why we should ask, where one should experience and learn that, and how to teach it |data=2 de novembro de 2017 |publicado=Springer |series=ICME-13 Monographs |paginas=63–77 |conferencia=Proceedings of the 13th International Congress on Mathematical Education |doi=10.1007/978-3-319-62597-3_5 |isbn=978-3-319-62596-6}}</ref> |
|||
[[Aristóteles]] definiu a matemática como “a ciência da [[quantidade]]” e esta definição prevaleceu até o século XVIII. No entanto, ele também observou que o foco apenas na quantidade pode não distinguir a matemática de ciências como a [[física]]; em sua opinião, a abstração e o estudo da quantidade como uma propriedade "separável no pensamento" das instâncias reais diferenciam a matemática.<ref name="Franklin">{{Citar livro|url={{GBurl|id=mbn35b2ghgkC|p=104}}|título=Philosophy of Mathematics|ultimo=Franklin|primeiro=James|data=2009|editora=Elsevier|páginas=104–106|isbn=978-0-08-093058-9|autorlink=James Franklin (philosopher)|acessodata=20 de junho de 2015}}</ref> No século XIX, quando os matemáticos começaram a abordar temas que não têm uma relação clara com a realidade física, como os [[Conjunto infinito|conjuntos infinitos]], foram dadas uma variedade de novas definições.<ref name="Cajori">{{Citar livro|url={{GBurl|id=mGJRjIC9fZgC|p=285}}|título=A History of Mathematics|ultimo=Cajori|primeiro=Florian|editora=American Mathematical Society (1991 reprint)|ano=1893|páginas=285–286|isbn=978-0-8218-2102-2|autorlink=Florian Cajori|acessodata=20 de junho de 2015}}</ref> |
|||
Outra abordagem para definir matemática é fazer uso de seus métodos. Assim, uma área de estudo pode ser qualificada como matemática desde que possa provar [[teoremas]], ou seja, afirmações cuja validade depende de uma prova, isto é, de uma [[dedução]] puramente [[lógica]].<ref>{{Citar periódico |url=https://cds.cern.ch/record/280311 |título=The Methodology of Mathematics |data=Janeiro de 2000 |acessodata=25 de novembro de 2022 |periódico=The Mathematical Gazette |número=485 |ultimo=Brown |primeiro=Ronald |ultimo2=Porter |primeiro2=Timothy |paginas=321–334 |doi=10.2307/3618304 |jstor=3618304 |arquivourl=https://web.archive.org/web/20230323164159/https://cds.cern.ch/record/280311 |arquivodata=23 de março de 2023 |volume=79}}</ref> Outros, no entanto, assumem a perspectiva de que a matemática é uma investigação da [[teoria axiomática]] dos conjuntos, já que este estudo é atualmente uma disciplina fundamental para grande parte da matemática moderna.<ref>{{Citar periódico |url=https://www.researchgate.net/publication/290955899 |título=Defining mathematics |acessodata=25 de novembro de 2022 |periódico=Acta Academica |número=4 |ultimo=Strauss |primeiro=Danie |ano=2011 |paginas=1–28 |volume=43}}</ref> |
|||
=== Rigor === |
|||
O raciocínio matemático requer [[rigor]]. Isso significa que as definições devem ser absolutamente inequívocas e as [[Prova matemática|provas]] devem ser redutíveis a uma sucessão de aplicações de [[Regra de inferência|regras de inferência]],{{Nre|Isto não significa tornar explícitas todas as regras de inferência utilizadas. Pelo contrário, isto geralmente é impossível, sem [[computadores]] e [[assistentes de prova]]. Mesmo com esta tecnologia moderna, podem ser necessários anos de trabalho humano para redigir uma prova matemática completamente detalhada.}} sem qualquer uso de evidência empírica e [[intuição]].{{Nre|Isto não significa que a evidência empírica e a intuição não sejam necessárias para escolher os teoremas a provar e para os provar.}}<ref>{{Citar periódico |url=https://www.yacinhamami.com/wp-content/uploads/2019/12/Hamami-2019-Mathematical-Rigor-and-Proof.pdf |título=Mathematical Rigor and Proof |data=Junho de 2022 |acessodata=21 de novembro de 2022 |periódico=The Review of Symbolic Logic |número=2 |ultimo=Hamami |primeiro=Yacin |paginas=409–449 |doi=10.1017/S1755020319000443 |arquivourl=https://web.archive.org/web/20221205114343/https://www.yacinhamami.com/wp-content/uploads/2019/12/Hamami-2019-Mathematical-Rigor-and-Proof.pdf |arquivodata=5 de dezembro de 2022 |volume=15}}</ref> O raciocínio rigoroso não é específico da matemática, mas o padrão de rigor é muito mais alto do que em outros campos de estudo. Apesar da concisão da matemática, provas rigorosas podem exigir centenas de páginas para serem expressas. O surgimento de provas assistidas por computador permitiu que os comprimentos das provas se expandissem ainda mais,{{Nre|Para considerar como confiável um grande cálculo que ocorre em uma prova, geralmente são necessários dois cálculos usando um software independente}}<ref>{{Harvnb|Peterson|1988|p=4}}: "A few complain that the computer program can't be verified properly." (in reference to the Haken–Apple proof of the [[Teorema das quatro cores|Four Color Theorem]])</ref> como o teorema de Feit-Thompson de 255 páginas.{{Nre|O livro que contém a prova completa tem mais de mil páginas.}} O resultado desta tendência é uma filosofia da prova quase empirista, mas que não pode ser considerada infalível.<ref name="Kleiner_1991"/> |
|||
O conceito de rigor na matemática remonta à [[Grécia Antiga]], onde a sociedade incentivava o [[raciocínio lógico]] e [[dedutivo]]. No entanto, o rigor tenderia a desencorajar a exploração de novas abordagens, tais como [[números irracionais]] e conceitos de [[infinito]]. O método de demonstração de provas rigorosas foi aprimorado ao longo do século XVI através do uso de notação simbólica. Durante o século XVIII, a transição social permitiu que os matemáticos passassem a ganhar seu sustento através do ensino, o que levou a uma reflexão mais cuidadosa sobre os conceitos subjacentes à matemática e produziu abordagens mais rigorosas durante a transição de métodos geométricos para provas algébricas e depois aritméticas.<ref name="Kleiner_1991"/> |
|||
No final do século XIX, parecia que as definições dos conceitos básicos da matemática não eram suficientemente precisas para evitar paradoxos ([[geometria não euclidiana]] e [[função de Weierstrass]]) e contradições ([[paradoxo de Russell]]), o que foi resolvido pela inclusão de axiomas nas regras de inferência [[Apodicidade|apodítica]] das teorias matemáticas; a reintrodução do método axiomático iniciado pelos antigos gregos antigos.<ref name="Kleiner_1991"/> "Rigor" não é mais um conceito relevante em matemática, pois uma prova ou é correta ou é errônea, sendo que uma "prova rigorosa" é simplesmente um [[pleonasmo]]. Onde um conceito especial de rigor é aceito é nos aspectos socializados de uma prova, onde pode ser comprovadamente refutado por outros matemáticos. Depois de uma prova ter sido aceita por muitos anos ou mesmo décadas, ela pode então ser considerada confiável.<ref>{{Citar periódico |título=On the Reliability of Mathematical Proofs |periódico=Philosophy of Mathematics |publicado=Revue Internationale de Philosophie |número=167 (4) |ultimo=Perminov |primeiro=V. Ya. |ano=1988 |paginas=500–508 |volume=42}}</ref> No entanto, o conceito de “rigor” ainda pode continuar sendo útil para ensinar aos iniciantes o que é uma prova matemática.<ref>{{Citar periódico |título=Teachers' perceptions of the official curriculum: Problem solving and rigor |periódico=International Journal of Educational Research |ultimo=Davis |primeiro=Jon D. |ultimo2=McDuffie |primeiro2=Amy Roth |ano=2019 |paginas=91–100 |doi=10.1016/j.ijer.2018.10.002 |ultimo3=Drake |primeiro3=Corey |ultimo4=Seiwell |primeiro4=Amanda L. |volume=93}}</ref> |
|||
== Treinamento e prática == |
|||
=== Educação === |
|||
{{AP|Educação matemática|STEM}} |
|||
A matemática tem uma capacidade evidente de cruzar fronteiras culturais e períodos de tempo. Como atividade humana, a prática da matemática tem um aspecto social, que inclui [[Educação matemática|educação]], [[Matemático|profissão]], reconhecimento, popularização e assim por diante. Na educação, a matemática é uma parte central do currículo e constitui um elemento importante das disciplinas acadêmicas do grupo [[STEM]]. Carreiras proeminentes para matemáticos profissionais incluem [[Professor|professor de matemática]], [[estatístico]], [[atuário]], [[analista financeiro]], [[economista]], [[Contabilista|contador]], [[Consultoria em tecnologia da informação|consultor de informática]], entre outras.<ref>{{Citar livro|url={{GBurl|id=1cEYEAAAQBAJ|p=3}}|título=Mathematicians and Statisticians: A Practical Career Guide|ultimo=Endsley|primeiro=Kezia|editora=Rowman & Littlefield|ano=2021|series=Practical Career Guides|páginas=1–3|isbn=978-1-5381-4517-3|acessodata=29 de novembro de 2022}}</ref> |
|||
Evidências arqueológicas mostram que o ensino da matemática ocorreu já no [[segundo milênio a.C.]], na [[antiga Babilônia]].<ref>{{Citar livro|título=The Oxford Handbook of the History of Mathematics|ultimo=Robson|primeiro=Eleanor|editora=OUP Oxford|ano=2009|editor-sobrenome=Robson|capitulo=Mathematics education in an Old Babylonian scribal school|isbn=978-0-19-921312-2|autorlink=Eleanor Robson|acessodata=24 de novembro de 2022|editor-sobrenome2=Stedall|editor-link2=Jackie Stedall}}</ref> Evidências comparáveis foram descobertas nos escribas no [[Antigo Oriente Próximo]] e depois no [[mundo greco-romano]], começando por volta do ano 300 a.C..<ref>{{Citar livro|título=Handbook on the History of Mathematics Education|ultimo=Bernard|primeiro=Alain|ultimo2=Proust|primeiro2=Christine|ultimo3=Ross|primeiro3=Micah|editora=Springer|ano=2014|editor-sobrenome=Karp|páginas=27–53|capitulo=Mathematics Education in Antiquity|doi=10.1007/978-1-4614-9155-2_3|isbn=978-1-4614-9154-5|editor-sobrenome2=Schubring|local-publicação=Nova York}}</ref> O livro didático de matemática mais antigo conhecido é o [[Papiro de Rhind]], datado de {{Circa|1650 a.C.}} no [[Egito Antigo]].<ref>{{Citar periódico |título=The World's First Mathematics Textbook |data=Abril de 2002 |periódico=Math Horizons |publicado=Taylor & Francis, Ltd. |número=4 |ultimo=Dudley |primeiro=Underwood |paginas=8–11 |doi=10.1080/10724117.2002.11975154 |jstor=25678363 |volume=9}}</ref> Devido à escassez de livros, os ensinamentos matemáticos na [[Índia Antiga]] foram repassados através da [[tradição oral]] memorizada desde o [[Civilização védica|período védico]] ({{Circa|1500|500 BCE}}-500 a.C.).<ref>{{Citar conferência |ultimo=Subramarian |primeiro=F. |url=http://hpm2012.onpcs.com/Proceeding/OT2/T2-10.pdf |titulo=Indian pedagogy and problem solving in ancient Thamizhakam |acessodata=29 de novembro de 2022 |conferencia=History and Pedagogy of Mathematics conference, July 16–20, 2012 |arquivourl=https://web.archive.org/web/20221128082654/http://hpm2012.onpcs.com/Proceeding/OT2/T2-10.pdf |arquivodata=28 de novembro de 2022}}</ref> Na [[História da China|China Imperial,]] durante a [[dinastia Tang]] (618-907 d.C.), um currículo de matemática foi adotado para [[Exames imperiais|concursos públicos]] para ingressar na burocracia estatal.<ref>{{Citar livro|url=https://scholar.archive.org/work/3fb5lb2qsfg35gf2cv6viaydny/access/wayback/http://hkumath.hku.hk:80/~mks/Chapter%206-Siu.pdf|título=How Chinese Learn Mathematics|ultimo=Siu|primeiro=Man Keung|ano=2004|series=Series on Mathematics Education|volume=1|páginas=157–185|capitulo=Official Curriculum in Mathematics in Ancient China: How did Candidates Study for the Examination?|doi=10.1142/9789812562241_0006|isbn=978-981-256-014-8|acessodata=26 de novembro de 2022}}</ref> |
|||
Após a [[Idade das trevas|Idade das Trevas]], a educação matemática na Europa era ministrada por escolas religiosas como parte do [[Quadrívio]]. A instrução formal em [[pedagogia]] começou nas escolas [[Companhia de Jesus|jesuítas]] ao longo dos séculos XVI e XVII. A maior parte do currículo matemático, no entanto, permaneceu em um nível básico e prático até o século XIX, quando começou a florescer na [[França]] e na [[Alemanha]]. O periódico mais antigo abordando o ensino de matemática foi ''[[L'Enseignement Mathématique]]'', que começou a ser publicado no ano de 1899.<ref>{{Citar periódico |título=The History of Mathematical Education |periódico=The American Mathematical Monthly |publicado=Taylor & Francis, Ltd. |número=1 |ultimo=Jones |primeiro=Phillip S. |ano=1967 |paginas=38–55 |doi=10.2307/2314867 |jstor=2314867 |volume=74}}</ref> Os avanços do [[mundo ocidental]] na [[ciência]] e na [[tecnologia]] levaram ao estabelecimento de sistemas educativos centralizados em muitos [[Estados-nação]], sendo a matemática um componente central {{Mdash}} inicialmente por conta das suas aplicações militares.<ref>{{Citar periódico |título=Introduction: the history of mathematics teaching. Indicators for modernization processes in societies |data=Agosto de 2012 |periódico=ZDM Mathematics Education |número=4 |ultimo=Schubring |primeiro=Gert |ultimo2=Furinghetti |primeiro2=Fulvia |paginas=457–459 |doi=10.1007/s11858-012-0445-7 |ultimo3=Siu |primeiro3=Man Keung |volume=44 |doi-access=free}}</ref> Embora o conteúdo dos cursos varie, atualmente quase todos os países ensinam matemática aos seus alunos.<ref>{{Citar livro|url=https://files.eric.ed.gov/fulltext/ED610099.pdf|título=TIMSS 2019 International Results in Mathematics and Science|ultimo=von Davier|primeiro=Matthias|ultimo2=Foy|primeiro2=Pierre|ultimo3=Martin|primeiro3=Michael O.|ultimo4=Mullis|primeiro4=Ina V.S.|editora=TIMSS & PIRLS International Study Center, Lynch School of Education and Human Development and International Association for the Evaluation of Educational Achievement|ano=2020|língua=en-US|capitulo=Examining eTIMSS Country Differences Between eTIMSS Data and Bridge Data: A Look at Country-Level Mode of Administration Effects|isbn=978-1-889938-54-7|acessodata=29 de novembro de 2022|arquivourl=https://web.archive.org/web/20221129163908/https://files.eric.ed.gov/fulltext/ED610099.pdf|arquivodata=29 de novembro de 2022}}</ref> |
|||
Durante a escola, as capacidades matemáticas e as expectativas positivas têm uma forte associação com o interesse profissional na área. Fatores extrínsecos, como apoio de professores, pais e grupos de pares, podem influenciar o nível de interesse pela matemática.<ref>{{Citar periódico |url=https://www.academia.edu/download/45974312/j.2161-0045.2012.00001.x20160526-3995-67kydl.pdf |título=Social Cognitive Factors, Support, and Engagement: Early Adolescents' Math Interests as Precursors to Choice of Career |data=Março de 2012 |acessodata=29 de novembro de 2022 |periódico=The Career Development Quarterly |número=1 |ultimo=Rowan-Kenyon |primeiro=Heather T. |ultimo2=Swan |primeiro2=Amy K. |paginas=2–15 |doi=10.1002/j.2161-0045.2012.00001.x |arquivourl=https://web.archive.org/web/20231122212933/https://d1wqtxts1xzle7.cloudfront.net/45974312/j.2161-0045.2012.00001.x20160526-3995-67kydl-libre.pdf?1464293840=&response-content-disposition=inline%3B+filename%3DSocial_Cognitive_Factors_Support_and_Eng.pdf&Expires=1700692172&Signature=cs9KfTPxoPh859wY~ExtJyAl9NpYb3X-2P4rDel1Z3z7DwehsHLRggoZtgi1pMsamxYobu9dVK4G7OsqfvNxcuwz3uKh1pnCMZQEz~ahVtPb4kvN-4dmwExJplzoxWu31o3SJOfuBt0GGE-0Hl8eLfPBg5agmtkjSwAWQwlqGrjp3YgYZGjbNxOEAM4t1l4qvoWXidWvSHHcEUNvlKYwCDvG0~QhGTmA6ldxmfS1ovf0adog-qqvjGxxJuSjtP6O8zCTwkPXYwi2e8giI0H6b5fNarHc-2q~-NRnVVtYKhvSBcwC22kNZoA7s8sp8ix9KIdM3uxiUIBRBRC-4aaVoQ__&Key-Pair-Id=APKAJLOHF5GGSLRBV4ZA |arquivodata=22 de novembro de 2023 |ultimo3=Creager |primeiro3=Marie F. |volume=60}}</ref> Alguns alunos que estudam matemática podem desenvolver apreensão ou medo em relação ao seu desempenho na matéria, o que é conhecido como [[ansiedade matemática]] ou fobia matemática e é considerado o mais proeminente dos distúrbios que afetam o desempenho acadêmico. Isto pode se desenvolver devido a vários fatores, como atitudes dos pais e professores, estereótipos sociais e características pessoais. A ajuda para neutralizar este problema pode advir de mudanças nas abordagens instrucionais, de interações com pais e professores e de tratamentos personalizados para cada estudante.<ref>{{Citar periódico |título=Spotlight on math anxiety |periódico=Psychology Research and Behavior Management |ultimo=Luttenberger |primeiro=Silke |ultimo2=Wimmer |primeiro2=Sigrid |ano=2018 |paginas=311–322 |doi=10.2147/PRBM.S141421 |pmc=6087017 |pmid=30123014 |ultimo3=Paechter |primeiro3=Manuela |volume=11 |doi-access=free}}</ref> |
|||
=== Psicologia (estética, criatividade e intuição) === |
|||
A validade de um teorema matemático depende apenas do rigor da sua prova, que teoricamente poderia ser feita automaticamente por um [[programa de computador]]. Isto não significa que não há lugar para criatividade num trabalho matemático. Pelo contrário, muitos resultados matemáticos importantes (teoremas) são soluções de problemas que outros matemáticos não conseguiram resolver e a invenção de uma forma de resolução pode ser uma forma fundamental do processo de resolução.<ref>{{Citar periódico |título=The Outlook of the Mathematicians' Creative Processes |data=2 de junho de 2015 |periódico=Procedia - Social and Behavioral Sciences |ultimo=Yaftian |primeiro=Narges |paginas=2519–2525 |doi=10.1016/j.sbspro.2015.04.617 |volume=191 |doi-access=free}}</ref><ref>{{Citar periódico |título=The Frontage of Creativity and Mathematical Creativity |data=10 de outubro de 2013 |periódico=Procedia - Social and Behavioral Sciences |ultimo=Nadjafikhah |primeiro=Mehdi |ultimo2=Yaftian |primeiro2=Narges |paginas=344–350 |doi=10.1016/j.sbspro.2013.07.101 |volume=90 |doi-access=free}}</ref> Um exemplo extremo é o teorema de [[Roger Apéry]], cujo autor forneceu apenas as ideias para uma prova e a prova formal foi dada apenas alguns meses depois por três outros matemáticos.<ref>{{Citar periódico |url=http://pracownicy.uksw.edu.pl/mwolf/Poorten_MI_195_0.pdf |título=A proof that Euler missed... Apéry's Proof of the irrationality of ζ(3) |acessodata=22 de novembro de 2022 |periódico=The Mathematical Intelligencer |número=4 |ultimo=van der Poorten |primeiro=A. |ano=1979 |paginas=195–203 |doi=10.1007/BF03028234 |arquivourl=https://web.archive.org/web/20150906015716/http://pracownicy.uksw.edu.pl/mwolf/Poorten_MI_195_0.pdf |arquivodata=6 de setembro de 2015 |volume=1}}</ref> |
|||
A criatividade e o rigor não são os únicos aspectos psicológicos da atividade dos matemáticos. Alguns deles podem ver a sua atividade como um jogo. Este aspecto da atividade matemática é enfatizado na [[matemática recreativa]].<ref>{{Citar livro|url={{GBurl|id=AZlwAAAAQBAJ|pg=PR13}}|título=Famous Puzzles of Great Mathematicians|ultimo=Petkovi|primeiro=Miodrag|data=2 de setembro de 2009|editora=American Mathematical Society|páginas=xiii–xiv|isbn=978-0-8218-4814-2|acessodata=25 de novembro de 2022}}</ref> Os matemáticos podem encontrar um valor [[Estética|estético]] para o seu campo de estudo. Assim como a [[beleza]], a matemática é difícil de definir, está comumente relacionada à ''elegância'', que envolve qualidades como [[simplicidade]], [[simetria]], [[Completude (lógica)|completude]] e generalidade. [[G. H. Hardy]], em sua obra ''[[Apologia do Matemático|Apologia do Matemático,]]'' expressou a crença de que as considerações estéticas são, em si, suficientes para justificar o estudo da [[matemática pura]]. Ele também identificou outros critérios, como [[significância]], imprevisibilidade e inevitabilidade, que contribuem para a estética matemática.<ref>{{Citar livro|url=https://archive.org/details/hardy_annotated/|título=A Mathematician's Apology|ultimo=Hardy|primeiro=G. H.|editora=Cambridge University Press|ano=1940|isbn=978-0-521-42706-7|autorlink=G. H. Hardy|acessodata=22 de novembro de 2022}} See also ''[[Apologia do Matemático|A Mathematician's Apology]]''.</ref> [[Paul Erdős]] expressou este sentimento de forma mais irônica ao falar de "O Livro", uma suposta coleção divina das mais belas provas. A obra literária ''[[Provas conforme O Livro]]'' de 1998, inspirado no livro de Erdős, é uma coleção de argumentos matemáticos particularmente sucintos e reveladores. Alguns exemplos de resultados particularmente elegantes incluídos são a prova de Euclides de que existem infinitos [[números primos]] e a [[transformada rápida de Fourier]] para [[Análise harmónica|análise harmônica]].<ref>{{Citar periódico |título=Reflections on Paul Erdős on His Birth Centenary, Part II |data=Março de 2015 |periódico=Notices of the American Mathematical Society |número=3 |ultimo=Alon |primeiro=Noga |ultimo2=Goldston |primeiro2=Dan |editor-sobrenome=Krishnaswami |editor-nome=Alladi |paginas=226–247 |doi=10.1090/noti1223 |ultimo3=Sárközy |primeiro3=András |ultimo4=Szabados |primeiro4=József |ultimo5=Tenenbaum |primeiro5=Gérald |ultimo6=Garcia |primeiro6=Stephan Ramon |ultimo7=Shoemaker |primeiro7=Amy L. |editor-sobrenome2=Krantz |editor-nome2=Steven G. |volume=62 |doi-access=free}}</ref> |
|||
Alguns acham que considerar a matemática uma ciência é subestimar a sua arte e história nas sete [[artes liberais]] tradicionais.<ref>See, for example [[Bertrand Russell]]'s statement "Mathematics, rightly viewed, possesses not only truth, but supreme beauty ..." in his {{Citar livro|título=History of Western Philosophy|ano=1919}}</ref> Uma forma desta diferença de [[ponto de vista]] se manifestar é no debate filosófico sobre se os resultados matemáticos são ''criados'' (como na arte) ou ''descobertos'' (como na ciência).<ref name="borel">{{Citar periódico |título=Mathematics: Art and Science |periódico=The Mathematical Intelligencer |publicado=Springer |número=4 |ultimo=Borel |primeiro=Armand |autorlink=Armand Borel |ano=1983 |paginas=9–17 |doi=10.4171/news/103/8 |issn=1027-488X |volume=5 |doi-access=free}}</ref> |
|||
== Impacto cultural == |
|||
=== Expressão artística === |
|||
[[Ficheiro:Julia_set_(highres_01).jpg|miniaturadaimagem|[[Fractal]] com simetria de escala e simetria central]] |
|||
[[Notas musicais]] que soam bem juntas para um ouvido ocidental são sons cujas [[Frequência|frequências]] fundamentais de vibração estão em proporções simples. Por exemplo, uma oitava duplica a frequência e uma [[quinta justa]] multiplica-a por <math>\frac{3}{2}</math>.<ref>{{Citar periódico |título=Musical intervals and simple number ratios |data=outubro de 1959 |periódico=Journal of Research in Music Education |número=2 |ultimo=Cazden |primeiro=Norman |paginas=197–220 |doi=10.1177/002242945900700205 |jstor=3344215 |volume=7}}</ref><ref>{{Citar periódico |título=Modern mathematics and music |data=Outubro de 1967 |periódico=The Mathematical Gazette |publicado=Cambridge University Press ({CUP}) |número=377 |ultimo=Budden |primeiro=F. J. |paginas=204–215 |doi=10.2307/3613237 |jstor=3613237 |volume=51}}</ref> |
|||
Os humanos, assim como alguns outros animais, consideram os padrões simétricos mais bonitos.<ref>{{Citar periódico |url=https://www.nature.com/articles/372169a0 |título=Symmetry, beauty and evolution |data=Novembro de 1994 |acessodata=29 de dezembro de 2022 |periódico=Nature |número=6502 |ultimo=Enquist |primeiro=Magnus |ultimo2=Arak |primeiro2=Anthony |paginas=169–172 |lingua=en |bibcode=1994Natur.372..169E |doi=10.1038/372169a0 |issn=1476-4687 |pmid=7969448 |arquivourl=https://web.archive.org/web/20221228052049/https://www.nature.com/articles/372169a0 |arquivodata=28 de dezembro de 2022 |volume=372}}</ref> Matematicamente, as simetrias de um objeto formam um grupo conhecido como [[grupo de simetria]].<ref>{{Citar web|ultimo=Hestenes|primeiro=David|url=http://geocalc.clas.asu.edu/pdf-preAdobe8/SymmetryGroups.pdf|titulo=Symmetry Groups|data=1999|acessodata=29 de dezembro de 2022|website=geocalc.clas.asu.edu|arquivourl=https://web.archive.org/web/20230101210124/http://geocalc.clas.asu.edu/pdf-preAdobe8/SymmetryGroups.pdf|arquivodata=1 de janeiro de 2023|urlmorta=live}}</ref> |
|||
Por exemplo, o grupo subjacente à simetria do espelho é o [[grupo cíclico]] de dois elementos, <math>\mathbb{Z}/2\mathbb{Z}</math> . Um [[teste de Rorschach]] é uma figura invariante por esta simetria,<ref>{{Citar enciclopédia|ultimo=Bender|primeiro=Sara|titulo=The Rorschach Test|data=Setembro de 2020|enciclopédia=The Wiley Encyclopedia of Personality and Individual Differences: Measurement and Assessment|publicado=Wiley|editor-sobrenome=Carducci|paginas=367–376|doi=10.1002/9781119547167.ch131|isbn=978-1-119-05751-2|editor-sobrenome2=Nave|editor-nome2=Christopher S.|editor-sobrenome3=Mio|editor-sobrenome4=Riggio|editor-nome4=Ronald E.}}</ref> assim como os corpos de [[borboletas]] e animais em geral (pelo menos na superfície).<ref>{{Citar livro|título=Symmetry|ultimo=Weyl|primeiro=Hermann|editora=Princeton University Press|ano=2015|series=Princeton Science Library|volume=47|isbn=978-1-4008-7434-7|autorlink=Hermann Weyl}}</ref> As ondas na superfície do mar possuem simetria de translação: mover o ponto de vista pela distância entre as cristas das ondas não altera a visão do mar. [[Fractal|Fractais]] possuem [[autossimilaridade]].<ref>{{Citar web|ultimo=Bradley|primeiro=Larry|url=https://www.stsci.edu/~lbradley/seminar/fractals.html|titulo=Fractals – Chaos & Fractals|data=2010|acessodata=29 de dezembro de 2022|website=www.stsci.edu|arquivourl=https://web.archive.org/web/20230307054609/https://www.stsci.edu/~lbradley/seminar/fractals.html|arquivodata=7 de março de 2023|urlmorta=live}}</ref><ref>{{Citar web|url=https://math.bu.edu/DYSYS/chaos-game/node5.html|titulo=Self-similarity|acessodata=29 de dezembro de 2022|website=math.bu.edu|arquivourl=https://web.archive.org/web/20230302132911/http://math.bu.edu/DYSYS/chaos-game/node5.html|arquivodata=2 de março de 2023|urlmorta=live}}</ref> |
|||
=== Popularização === |
|||
A matemática popular é o ato de apresentar a matemática sem termos técnicos.<ref>{{Citar conferência |ultimo=Kissane |primeiro=Barry |url=https://researchrepository.murdoch.edu.au/id/eprint/6242/ |titulo=Popular mathematics |data=Julho de 2009 |acessodata=29 de dezembro de 2022 |publicado=Australian Association of Mathematics Teachers |local=Fremantle, Western Australia |paginas=125–126 |conferencia=22nd Biennial Conference of The Australian Association of Mathematics Teachers |arquivourl=https://web.archive.org/web/20230307054610/https://researchrepository.murdoch.edu.au/id/eprint/6242/ |arquivodata=7 de março de 2023}}</ref> Apresentar matemática pode ser difícil, uma vez que o público em geral sofre de ansiedade matemática e os objetos matemáticos são altamente abstratos.<ref>{{Citar livro|url={{GBurl|id=-d3TBwAAQBAJ|dq="popular mathematics" analogies|p=2}}|título=Mathematics Today Twelve Informal Essays|ultimo=Steen|primeiro=L. A.|data=2012|editora=Springer Science & Business Media|língua=en|isbn=978-1-4613-9435-8|acessodata=3 de janeiro de 2023}}</ref> No entanto, a escrita matemática popular pode superar isto usando aplicativos ou referências culturais.<ref>{{Citar livro|url={{GBurl|id=9nGQDQAAQBAJ|dq="popular mathematics" analogies|p=331}}|título=The Best Writing on Mathematics 2016|ultimo=Pitici|primeiro=Mircea|data=2017|editora=Princeton University Press|língua=en|isbn=978-1-4008-8560-2|acessodata=3 de janeiro de 2023}}</ref> |
|||
== Prêmios == |
|||
[[Ficheiro:FieldsMedalFront.jpg|miniaturadaimagem| A frente da [[Medalha Fields]] com uma ilustração do [[polímata]] grego [[Arquimedes]]]] |
|||
O prêmio de maior prestígio em matemática é a [[Medalha Fields]],{{Sfn|Monastyrsky|2001|p=1|ps=: "The Fields Medal is now indisputably the best known and most influential award in mathematics."}}{{Sfn|Riehm|2002|pp=778–782}} criada em 1936 e concedida a cada quatro anos (exceto por volta da [[Frente Iugoslava|Segunda Guerra Mundial]]) a até quatro indivíduos.<ref>{{Citar web|url=https://www.mathunion.org/imu-awards/fields-medal|titulo=Fields Medal {{!}} International Mathematical Union (IMU)|acessodata=21 de fevereiro de 2022|website=www.mathunion.org|arquivourl=https://web.archive.org/web/20181226015744/https://www.mathunion.org/imu-awards/fields-medal|arquivodata=26 de dezembro de 2018|urlmorta=live}}</ref><ref name="StAndrews-Fields">{{Citar web|url=https://mathshistory.st-andrews.ac.uk/Honours/FieldsMedal/|titulo=Fields Medal|acessodata=21 de fevereiro de 2022|website=Maths History|lingua=en|arquivourl=https://web.archive.org/web/20190322134417/http://www-history.mcs.st-andrews.ac.uk/Honours/FieldsMedal.html|arquivodata=22 de março de 2019|urlmorta=live}}</ref> É considerado o equivalente matemático do [[Prêmio Nobel]].<ref name="StAndrews-Fields" /> |
|||
Outros prêmios de matemática de prestígio incluem:<ref>{{Citar web|url=https://mathshistory.st-andrews.ac.uk/Honours/|titulo=Honours/Prizes Index|acessodata=20 de fevereiro de 2023|editor=[[Universidade de St. Andrews]]|arquivourl=https://web.archive.org/web/20211217235828/https://mathshistory.st-andrews.ac.uk/Honours/|arquivodata=17 de dezembro de 2021|urlmorta=live}}</ref> |
|||
* O [[Prémio Abel|Prêmio Abel]], instituído em 2002<ref>{{Citar web|url=https://abelprize.no/page/about-abel-prize|titulo=About the Abel Prize|acessodata=23 de janeiro de 2022|publicado=The Abel Prize|arquivourl=https://web.archive.org/web/20220414060442/https://abelprize.no/page/about-abel-prize|arquivodata=14 de abril de 2022|urlmorta=live}}</ref> e concedido pela primeira vez em 2003;<ref>{{Citar enciclopédia|url=https://www.britannica.com/science/Abel-Prize|titulo=Abel Prize {{!}} mathematics award|acessodata=23 de janeiro de 2022|enciclopédia=Encyclopedia Britannica|lingua=en|arquivourl=https://web.archive.org/web/20200126120202/https://www.britannica.com/science/Abel-Prize|arquivodata=26 de janeiro de 2020|urlmorta=live}}</ref> |
|||
* A [[Medalha Chern]] pelo conjunto da obra, introduzida em 2009<ref>{{Citar web|url=https://www.mathunion.org/fileadmin/IMU/Prizes/Chern/Chern_MedalPress_Release_090601.pdf|titulo=Chern Medal Award|data=1 de junho de 2009|acessodata=21 de fevereiro de 2022|website=www.mathunion.org|arquivourl=https://web.archive.org/web/20090617012953/https://www.mathunion.org/fileadmin/IMU/Prizes/Chern/Chern_MedalPress_Release_090601.pdf|arquivodata=17 de junho de 2009|urlmorta=live}}</ref> e concedida pela primeira vez em 2010;<ref>{{Citar web|url=https://www.mathunion.org/imu-awards/chern-medal-award|titulo=Chern Medal Award|acessodata=23 de janeiro de 2022|publicado=International Mathematical Union (IMU)|arquivourl=https://web.archive.org/web/20100825071850/http://www.mathunion.org/general/prizes/chern/details|arquivodata=25 de agosto de 2010|urlmorta=live}}</ref> |
|||
* O [[Prêmio Leroy P. Steele|Prêmio]] [[American Mathematical Society|AMS]] Leroy P. Steele, concedido desde 1970;<ref>{{Citar web|url=https://mathshistory.st-andrews.ac.uk/Honours/AMSSteelePrize/|titulo=The Leroy P Steele Prize of the AMS|acessodata=17 de novembro de 2022|publicado=School of Mathematics and Statistics, University of St Andrews, Scotland|arquivourl=https://web.archive.org/web/20221117201134/https://mathshistory.st-andrews.ac.uk/Honours/AMSSteelePrize/|arquivodata=17 de novembro de 2022|urlmorta=live}}</ref> |
|||
* O [[Prêmio Wolf de Matemática]], também pelo conjunto da obra,<ref>{{Citar livro|url=https://www.worldscientific.com/worldscibooks/10.1142/4149|título=Wolf Prize in Mathematics|ultimo=Chern|primeiro=S. S.|ultimo2=Hirzebruch|primeiro2=F.|data=Setembro de 2000|língua=en|doi=10.1142/4149|isbn=978-981-02-3945-9|acessodata=21 de fevereiro de 2022|arquivourl=https://web.archive.org/web/20220221171351/https://www.worldscientific.com/worldscibooks/10.1142/4149|arquivodata=21 de fevereiro de 2022}}</ref> instituído em 1978.<ref>{{Citar web|url=https://wolffund.org.il/the-wolf-prize/|titulo=The Wolf Prize|acessodata=23 de janeiro de 2022|website=Wolf Foundation|lingua=en-US|arquivourl=https://web.archive.org/web/20200112205029/https://wolffund.org.il/the-wolf-prize/|arquivodata=12 de janeiro de 2020|urlmorta=live}}</ref> |
|||
Uma famosa lista de 23 [[Problema em aberto|problemas em aberto]], chamada "[[problemas de Hilbert]]", foi compilada em 1900 pelo matemático alemão [[David Hilbert]].<ref name=":0">{{Citar web|url=https://www.simonsfoundation.org/2020/05/06/hilberts-problems-23-and-math/|titulo=Hilbert's Problems: 23 and Math|data=6 de maio de 2020|acessodata=23 de janeiro de 2022|website=Simons Foundation|lingua=en-US|arquivourl=https://web.archive.org/web/20220123011430/https://www.simonsfoundation.org/2020/05/06/hilberts-problems-23-and-math/|arquivodata=23 de janeiro de 2022|urlmorta=live}}</ref> Esta lista alcançou grande celebridade entre os matemáticos<ref>{{Citar livro|url={{GBurl|id=1rjnCwAAQBAJ}}|título=In the Light of Logic|ultimo=Feferman|primeiro=Solomon|editora=Oxford University Press|ano=1998|series=Logic and Computation in Philosophy series|páginas=3–27|capitulo=Deciding the undecidable: Wrestling with Hilbert's problems|isbn=978-0-19-508030-8|autorlink=Solomon Feferman|acessodata=29 de novembro de 2022}}</ref> e, desde 2022, pelo menos treze dos problemas (dependendo de como alguns são interpretados) foram resolvidos.<ref name=":0" /> |
|||
Uma nova lista de sete problemas importantes, intitulada "[[Problemas do Prémio Millennium|Problemas do Prêmio Millennium]]", foi publicada no ano 2000. Apenas uma delas, a [[Hipótese de Riemann]], duplica um dos problemas de Hilbert. Uma solução para qualquer um desres problemas acarreta uma recompensa de 1 milhão de dólares.<ref>{{Citar web|url=http://www.claymath.org/millennium-problems/millennium-prize-problems|titulo=The Millennium Prize Problems|acessodata=23 de janeiro de 2022|publicado=Clay Mathematics Institute|arquivourl=https://web.archive.org/web/20150703184941/http://www.claymath.org/millennium-problems/millennium-prize-problems|arquivodata=3 de julho de 2015|urlmorta=live}}</ref> Até hoje, apenas um destes problemas, a [[Conjectura de Poincaré]], foi resolvido.<ref>{{Citar web|url=http://www.claymath.org/millennium-problems|titulo=Millennium Problems|acessodata=23 de janeiro de 2022|publicado=Clay Mathematics Institute|arquivourl=https://web.archive.org/web/20181220122925/http://www.claymath.org/millennium-problems|arquivodata=20 de dezembro de 2018|urlmorta=live}}</ref> |
|||
== Ver também == |
|||
*[[Lista de constantes matemáticas]] |
|||
{{notas e referências}} |
|||
=== Bibliografia === |
|||
{{refbegin|30em}} |
|||
* {{cite book |last=Bouleau |first=Nicolas |title=Philosophie des mathématiques et de la modélisation: Du chercheur à l'ingénieur |publisher=L'Harmattan |year=1999 |isbn=978-2-7384-8125-2 |ref=harv}} |
|||
* {{cite book |last1=Boyer |first1=Carl Benjamin |author1-link=Carl Benjamin Boyer |title=A History of Mathematics |date=1991 |publisher=Wiley |location=Nova York |isbn=978-0-471-54397-8 |edition=2ª |url=https://archive.org/details/historyofmathema00boye/page/n3/mode/2up |chapter= |ref=harv}} |
|||
* {{cite book |last=Eves |first=Howard |author-link=Howard Eves |title=An Introduction to the History of Mathematics |edition=6th |publisher=Saunders |year=1990 |isbn=978-0-03-029558-4 |ref=harv}} |
|||
* {{cite book |last=Kleiner |first=Israel |editor-first1=Israel |editor-last1=Kleiner |year=2007 |title=A History of Abstract Algebra |publisher=Springer Science & Business Media |doi=10.1007/978-0-8176-4685-1 |isbn=978-0-8176-4684-4 |lccn=2007932362 |oclc=76935733 |s2cid=117392219 |url={{GBurl|id=RTLRBK-wj6wC}} |access-date=8 de fevereiro de 2024 |ref=harv}} |
|||
* {{cite book |last=Kline |first=Morris |author-link=Morris Kline |title=Mathematical Thought from Ancient to Modern Times |url=https://archive.org/details/mathematicalthou00klin |location=Nova York |publisher=Oxford University Press |edition=|year=1990 |isbn=978-0-19-506135-2 |ref=harv}} |
|||
* {{cite journal |last=Monastyrsky |first=Michael |url=http://www.fields.utoronto.ca/aboutus/FieldsMedal_Monastyrsky.pdf |year=2001 |title=Some Trends in Modern Mathematics and the Fields Medal |journal=CMS – Notes – de la SMC |volume=33 |issue=2–3 |publisher=Canadian Mathematical Society |access-date=28 de julho de 2006 |archive-date=13 de agosto de 2006 |archive-url=https://web.archive.org/web/20060813224844/http://www.fields.utoronto.ca/aboutus/FieldsMedal_Monastyrsky.pdf |urlmorta=live |ref=harv}} |
|||
* {{cite book |last=Oakley |first=Barbara |title=A Mind For Numbers: How to Excel at Math and Science (Even If You Flunked Algebra) |date=2014 |publisher=Penguin Random House |location=Nova York |url=https://archive.org/details/isbn_9780399165245|quote=A Mind for Numbers. |isbn=978-0-399-16524-5 |ref=harv}} |
|||
* {{cite journal |last=Peirce |first=Benjamin |author-link=Benjamin Peirce |pages=97–229 |title=Linear associative algebra |editor-link=Charles Sanders Peirce |editor-first=Charles Sanders |editor-last=Peirce |edition=Corrected, expanded, and annotated revision with an 1875 paper by B. Peirce and annotations by his son, C.S. Peirce, of the 1872 lithograph |journal=American Journal of Mathematics |volume=4 |year=1881 |url={{GBurl|id=De0GAAAAYAAJ|q=Peirce Benjamin Linear Associative Algebra|p=1}} |id=Corrected, expanded, and annotated revision with an 1875 paper by B. Peirce and annotations by his son, C. S. Peirce, of the 1872 lithograph ed. ''Google'' [{{GBurl|id=LQgPAAAAIAAJ|p=221}} Eprint] and as an extract, D. Van Nostrand, 1882, ''Google'' [https://archive.org/details/bub_gb_De0GAAAAYAAJ Eprint] |issue=1–4 |doi=10.2307/2369153 |jstor=2369153 |hdl=2027/hvd.32044030622997 |hdl-access=free |access-date=17 de novembro de 2020 |ref=harv}}. |
|||
* {{cite book |last=Peterson |first=Ivars |year=1988 |title=The Mathematical Tourist: Snapshots of Modern Mathematics |publisher=W. H. Freeman and Company |isbn=0-7167-1953-3 |lccn=87033078 |oclc=17202382 |ref=harv}} |
|||
* {{cite book |last=Popper |first=Karl R. |author-link=Karl Popper |title=In Search of a Better World: Lectures and Essays from Thirty Years |location=New York |publisher=Routledge |chapter=On knowledge |year=1995 |isbn=978-0-415-13548-1 |bibcode=1992sbwl.book.....P |url=https://archive.org/details/insearchofbetter00karl |ref=harv}} |
|||
* {{cite journal |last=Riehm |first=Carl |title=The Early History of the Fields Medal |journal=Notices of the AMS |volume=49 |issue=7 |pages=778–782 |date=Agosto de 2002 |url=https://www.ams.org/notices/200207/comm-riehm.pdf |access-date=2 de outubro de 2006 |archive-date=26 de outubro de 2006 |archive-url=https://web.archive.org/web/20061026000014/http://www.ams.org/notices/200207/comm-riehm.pdf |urlmorta=live |ref=harv}} |
|||
* {{cite journal |last=Sevryuk |first=Mikhail B. |date=Janeiro de 2006 |title=Book Reviews |journal=Bulletin of the American Mathematical Society|volume=43 |issue=1 |pages=101–109 |url=https://www.ams.org/bull/2006-43-01/S0273-0979-05-01069-4/S0273-0979-05-01069-4.pdf |access-date=24 de junho de 2006 |doi=10.1090/S0273-0979-05-01069-4 |archive-date=23 de julho de 2006 |archive-url=https://web.archive.org/web/20060723082901/http://www.ams.org/bull/2006-43-01/S0273-0979-05-01069-4/S0273-0979-05-01069-4.pdf |urlmorta=live |ref=harv}} |
|||
* {{cite book |last=Whittle |first=Peter |chapter=Almost home |editor-first=F.P. |editor-last=Kelly |year=1994 |title=Probability, statistics and optimisation: A Tribute to Peter Whittle |location=Chichester |publisher=John Wiley |isbn=978-0-471-94829-2 |pages=1–28 |chapter-url=http://www.statslab.cam.ac.uk/History/2history.html#6._1966--72:_The_Churchill_Chair |edition=previously "A realised path: The Cambridge Statistical Laboratory up to 1993 (revised 2002)" |urlmorta=live |archive-url=https://web.archive.org/web/20131219080017/http://www.statslab.cam.ac.uk/History/2history.html#6._1966--72:_The_Churchill_Chair |archive-date=19 de dezembro de 2013 |ref=harv}} |
|||
{{refend}} |
|||
== Ligações externas == |
== Ligações externas == |
||
* [http://www.impa.br/ Instituto de Matemática Pura e Aplicada (IMPA), Brasil] |
* [http://www.impa.br/ Instituto de Matemática Pura e Aplicada (IMPA), Brasil] |
||
{{Matemática2}}{{Ciências}} |
|||
{{Matemática2}} |
|||
{{Controle de autoridade}}{{Portal3|Matemática}} |
|||
{{Ciências}} |
|||
{{Controle de autoridade}} |
|||
{{Portal3|Matemática}} |
|||
[[Categoria:Matemática| ]] |
[[Categoria:Matemática| ]] |
||
Revisão das 06h28min de 5 de março de 2024
Matemática é uma área do conhecimento que inclui os tópicos dos números, fórmulas e estruturas relacionadas, formas e os espaços em que estão contidos, e quantidades e suas mudanças. Esses tópicos são representados na matemática moderna com as principais subdisciplinas da teoria dos números,[1] álgebra,[2] geometria[1] e análise,[3] respectivamente. No entanto, não há consenso entre os matemáticos sobre uma definição comum para a disciplina acadêmica que estudam.
Grande parte da atividade matemática envolve a descoberta de propriedades de objetos abstratos e o uso da razão pura para prová-las. Estes objetos consistem em abstrações da natureza ou — segundo a matemática moderna — entidades que são estipuladas por certas propriedades, chamadas axiomas. Uma prova matemática consiste em uma sucessão de aplicações de regras dedutivas a resultados já estabelecidos. Estes resultados incluem teoremas previamente provados, axiomas e — no caso de abstração da natureza — algumas propriedades básicas que são consideradas pontos de partida da teoria em consideração.[4]
A matemática é essencial nas ciências naturais, engenharia, medicina, finanças, ciências da computação e ciências sociais. Embora seja amplamente utilizada para modelar fenômenos, as verdades fundamentais da matemática são independentes de qualquer experimentação científica. Algumas áreas da matemática, como estatística e teoria dos jogos, são desenvolvidas em estreita correlação com suas aplicações e, portanto, são frequentemente agrupadas na matemática aplicada. Outros campos de estudo são desenvolvidos independentemente de qualquer aplicação (e por este motivo são chamados de matemática pura), mas muitas vezes encontram aplicações práticas posteriormente.[5][6]
Historicamente, o conceito de prova e o rigor matemático associado apareceram pela primeira vez na matemática grega, mais notavelmente na obra Os Elementos de Euclides.[7] Desde o seu início, a matemática foi dividida principalmente em geometria e aritmética (a manipulação de números naturais e frações), até os séculos XVI e XVII, quando a álgebra[a] e o cálculo infinitesimal foram introduzidos como novos campos. Desde então, a interação entre inovações matemáticas e descobertas científicas levou a um aumento correlacionado no desenvolvimento de ambas.[8] No final do século XIX, a crise fundamental da matemática levou à sistematização do método axiomático,[9] que anunciou um aumento dramático no número de áreas matemáticas e seus campos de aplicação.
Etimologia
A palavra matemática vem do grego antigo máthēma e significa "aquilo que se aprende",[10] "aquilo que se conhece", assim como "estudo" e "ciência". A palavra passou a ter o significado mais restrito e técnico de "estudo matemático" mesmo no período clássico.[b] Seu adjetivo é mathēmatikós (μαθηματικός), que significa "relacionado à aprendizagem" ou "estudioso", que também passou a significar "matemático".[14] Em particular, mathēmatikḗ tékhnē (μαθηματικὴ τέχνη; em latim: ars mathematica) significava "a arte matemática".[10]
Da mesma maneira, uma das duas principais escolas de pensamento do pitagorismo era conhecida em grego antigo como mathēmatikoi (μαθηματικοί) — que na época significava "alunos" ao invés do significado moderno dado ao termo "matemáticos". Os pitagóricos foram provavelmente os primeiros a restringir o uso da palavra apenas ao estudo da aritmética e da geometria. Na época de Aristóteles (384-322 a.C.) este significado foi totalmente estabelecido.[15]
Em latim até cerca de 1700, o termo matemática tinha como significado mais comum "astrologia" (ou às vezes "astronomia"); isto mudou gradualmente para o significado atual entre 1500 e 1800. Esta mudança resultou em vários erros de tradução: Por exemplo, a advertência de Santo Agostinho de que os cristãos deveriam tomar cuidado com os mathematici, que significa "astrólogos", às vezes é mal traduzida como uma condenação dos matemáticos.[16]
Áreas da matemática
Antes do período do Renascimento, a matemática era dividida em duas áreas principais: a aritmética, a manipulação dos números, e a geometria, o estudo das formas.[17] Alguns tipos de pseudociência, como a numerologia e a astrologia, não eram então claramente distinguidas da matemática.[18]
Durante o período do Renascimento, surgiram mais dois campos de estudo matemáticos. A notação deu origem à álgebra que, a grosso modo, consiste no estudo e na manipulação de fórmulas. O cálculo, que consiste nos dois subcampos diferencial e integral, é o estudo de funções contínuas que modelam as relações tipicamente não lineares entre quantidades representadas por variáveis. Esta divisão em quatro áreas principais – aritmética, geometria, álgebra, cálculo[19] – perdurou até o final do século XIX. Áreas como mecânica celeste e mecânica dos sólidos eram então estudadas por matemáticos, mas agora são consideradas pertencentes à física.[20] O tema da combinatória foi estudado durante grande parte da história registrada, mas não se tornou um ramo separado da matemática até o século XVII.[21]
No final do século XIX, a crise fundamental da matemática e a resultante sistematização do método axiomático levaram a uma explosão de novas áreas da matemática nunca antes vista.[22][9] A edição de 2020 da Classificação de Disciplinas de Matemática, por exemplo, contém nada menos que 63 áreas matemáticas consideradas de primeiro nível.[23] Algumas delas correspondem à divisão mais antiga, como é o caso da teoria dos números e da geometria. Várias outras têm "geometria" em seus nomes ou são comumente consideradas parte da geometria. Álgebra e cálculo não aparecem como áreas de primeiro nível, mas são campos divididos em várias áreas. Outras áreas de primeiro nível surgiram durante o século XX ou não eram consideradas anteriormente como parte da matemática, como a lógica e os fundamentos matemáticos.[24]
Teoria dos Números

A teoria dos números teve início com as primeiras manipulações dos números naturais e posteriormente expandiu-se para números inteiros e números racionais . Ela já foi chamada de aritmética, mas atualmente este termo é usado principalmente para se referir aos cálculos numéricos.[25] A teoria dos números remonta à antiga Babilônia e provavelmente à China Antiga. Dois proeminentes teóricos deste campo de estudo matemático foram os gregos Euclides e Diofanto de Alexandria.[26] O estudo moderno da teoria dos números na sua forma abstrata é amplamente atribuído a Pierre de Fermat e Leonhard Euler, mas este campo se concretizou totalmente com as contribuições do francês Adrien-Marie Legendre e do alemão Carl Friedrich Gauss.[27]
Muitos problemas numéricos têm soluções que requerem métodos sofisticados. Um exemplo proeminente é o Último Teorema de Fermat, conjectura descrita no ano de 1637 por Pierre de Fermat, mas que foi provada apenas em 1994 por Andrew Wiles, que usou ferramentas incluindo teoria de esquemas de geometria algébrica, teoria de categorias e álgebra homológica.[28] Outro exemplo é a Conjectura de Goldbach, que afirma que todo número inteiro par maior que 2 é a soma de dois números primos. Declarada em 1742 por Christian Goldbach, permanece sem comprovação, apesar de esforços consideráveis.[29]
A teoria dos números abrange inúmeras subáreas, como teoria analítica dos números, teoria algébrica dos números, geometria dos números (orientada a métodos), equações diofantinas e teoria da transcendência (orientada a problemas).[24]
Geometria

A geometria é um dos ramos mais antigos da matemática e começou com receitas empíricas sobre formas, como linhas, ângulos e círculos, que foram desenvolvidas principalmente para a topografia e a arquitetura, mas desde então floresceram em muitos outros subcampos.[30]
Uma inovação fundamental foi a introdução, pelos antigos gregos, do conceito de provas, que exige que cada afirmação seja provada. Por exemplo, não é suficiente verificar por medição que, digamos, dois comprimentos são iguais; sua igualdade deve ser provada através do raciocínio a partir de resultados previamente aceitos (teoremas) e de algumas afirmações básicas que não estão sujeitas a prova porque são evidentes (postulados) ou que fazem parte da definição do objeto de estudo (axiomas). Este princípio, fundamental para toda a matemática, foi elaborado pela primeira vez para a geometria e foi sistematizado por Euclides por volta do ano 300 a.C. em sua obra Os Elementos.[31][32]
A geometria euclidiana é o estudo das formas e seus arranjos construídos a partir de retas, planos e círculos no plano e no espaço euclidiano tridimensional.[c][30] Foi desenvolvida sem mudança de métodos ou escopo até o século XVII, quando René Descartes introduziu o que hoje é chamado de coordenadas cartesianas, o que constituiu uma grande mudança de paradigma: em vez de definir números reais como comprimentos de segmentos de reta (ver reta numérica), permitiu a representação de pontos usando suas coordenadas, que são números. A álgebra (e mais tarde o cálculo) pode, portanto, ser usada para resolver problemas geométricos. A geometria foi dividida em dois novos subcampos: geometria sintética, que utiliza métodos puramente geométricos, e geometria analítica, que utiliza coordenadas sistemicamente.[33] A geometria analítica permite o estudo de curvas não relacionadas a círculos e linhas. Tais curvas podem ser definidas como o gráfico de funções, cujo estudo levou à geometria diferencial. Elas também podem ser definidas como equações implícitas, muitas vezes equações polinomiais (que geraram a geometria algébrica). A geometria analítica também permite considerar espaços euclidianos superiores a três dimensões.[30]
A geometria analítica permite o estudo das curvas não relacionadas a círculos e linhas que podem ser definidas como o gráfico de funções, cujo estudo levou ao surgimento da área da geometria diferencial. Tais curvas também podem ser definidas como equações implícitas, muitas vezes equações polinomiais (que geraram a geometria algébrica). A geometria analítica também permite considerar espaços euclidianos superiores a três dimensões.[30]
No século XIX, os matemáticos descobriram geometrias não euclidianas, ou seja, que não seguem o postulado das paralelas. Ao questionar a verdade deste postulado, esta descoberta foi interpretada como uma adesão ao Paradoxo de Russell ao revelar a crise fundamental da matemática. Este aspecto da crise foi resolvido por meio da sistematização do método axiomático e pela noção de que a verdade dos axiomas escolhidos, na verdade, não é um problema matemático.[34][9] Por sua vez, o método axiomático permite o estudo de diversas geometrias obtidas quer pela alteração dos axiomas, quer pela consideração de propriedades que não mudam sob transformações específicas do espaço.[35]
As subáreas atuais da geometria incluem:[24]
- Geometria projetiva, introduzida no século XVI por Girard Desargues, estende a geometria euclidiana adicionando pontos impróprios nos quais linhas paralelas se cruzam. Isto simplifica muitos aspectos da geometria clássica, unificando os tratamentos para linhas paralelas e que se cruzam.
- Geometria afim, o estudo das propriedades relativas ao paralelismo e independentes do conceito de comprimento.
- Geometria diferencial, o estudo de curvas, superfícies e suas generalizações, que são definidas por meio de funções diferenciáveis.
- Teoria múltipla, o estudo de formas que não estão necessariamente incorporadas em um espaço maior.
- Geometria riemanniana, o estudo das propriedades de distância em espaços curvos.
- Geometria algébrica, o estudo de curvas, superfícies e suas generalizações, que são definidas por meio de polinômios.
- Topologia, estudo das propriedades que se mantêm sob deformações contínuas.
- Topologia algébrica, o uso em topologia de métodos algébricos, principalmente álgebra homológica.
- Geometria discreta, o estudo de configurações finitas em geometria.
- Geometria convexa, estudo de conjuntos convexos.
- Geometria complexa, a geometria obtida pela substituição de números reais por números complexos.
Álgebra


A álgebra é a arte de manipular equações e fórmulas. Diofanto (século III) e Alcuarismi (século IX) foram os dois principais precursores deste campo de estudo matemático.[37][38] O grego Diofanto resolveu algumas equações envolvendo números naturais desconhecidos ao deduzir novas relações até obter a solução. O persa Alcuarismi, por sua vez, introduziu métodos sistemáticos para transformar equações, como mover um termo de um lado de uma equação para o outro lado. O termo "álgebra" é derivado da palavra árabe al-jabr que significa 'a reunião de partes quebradas' que ele usou para nomear um desses métodos no título de seu tratado principal.[39]
A álgebra tornou-se uma área independente apenas com François Viète (1540-1603), que introduziu o uso de variáveis para representar números desconhecidos ou não especificados.[40]
Até o século XIX, a álgebra consistia principalmente no estudo de equações lineares (atualmente álgebra linear) e de equações polinomiais em uma única incógnita, que eram chamadas de equações algébricas (termo ainda em uso, embora possa ser ambíguo). Durante o século XIX, os matemáticos começaram a usar variáveis para representar outras coisas além dos números (como matrizes, inteiros modulares e transformações geométricas), nas quais generalizações de operações aritméticas são frequentemente válidas.[41] O conceito de estrutura algébrica aborda isto, consistindo em um conjunto cujos elementos não são especificados, em operações que atuam sobre os elementos do conjunto e em regras que essas operações devem seguir. O escopo da álgebra cresceu assim para incluir o estudo de estruturas algébricas. Este objeto da álgebra foi denominado álgebra moderna ou álgebra abstrata, conforme estabelecido pela influência e trabalhos da matemática alemã Emmy Noether.[42]
Alguns tipos de estruturas algébricas têm propriedades úteis e muitas vezes fundamentais em muitas áreas da matemática. Seu estudo tornou-se parte autônoma da álgebra e inclui vários campos de estudos:[24]
- teoria dos grupos;
- teoria de campo;
- espaços vetoriais, cujo estudo é essencialmente igual ao da álgebra linear;
- teoria dos anéis;
- a álgebra comutativa, que é o estudo dos anéis comutativos, inclui o estudo dos polinômios e é uma parte fundamental da geometria algébrica;
- álgebra homológica;
- Álgebra de Lie e teoria dos Grupos de Lie;
- Álgebra booliana, que é amplamente utilizada para o estudo da estrutura lógica de computadores.
O estudo de tipos de estruturas algébricas como objetos matemáticos é o propósito da álgebra universal e da teoria das categorias.[43] Esta última se aplica a todas as estruturas matemáticas (não apenas às algébricas). Na sua origem foi introduzida juntamente com a álgebra homológica por permitir o estudo algébrico de objetos não algébricos como espaços topológicos; esta área específica de aplicação é chamada de topologia algébrica.[44]
Cálculo e análise

O cálculo, anteriormente chamado de cálculo infinitesimal, foi introduzido de forma independente e simultânea por dois matemáticos do século XVII, Newton e Leibniz.[45] É fundamentalmente o estudo da relação de variáveis que dependem umas das outras. O cálculo foi expandido no século XVIII por Euler com a introdução do conceito de função e muitos outros resultados.[46]
Atualmente, “cálculo” refere-se principalmente à parte elementar desta teoria, e “análise” é comumente usada para partes avançadas. A análise é subdividida em análise real, onde as variáveis representam números reais, e análise complexa, onde as variáveis representam números complexos. Ela inclui muitas subáreas compartilhadas por outras áreas da matemática como:[24]
- Cálculo multivariável;
- Análise funcional, onde variáveis representam funções variáveis;
- Integração, teoria da medida e teoria do potencial, todas fortemente relacionadas com a teoria das probabilidades num continuum;
- Equações diferenciais ordinárias;
- Equações diferenciais parciais;
- Análise numérica, dedicada principalmente ao cálculo em computadores de soluções de equações diferenciais ordinárias e parciais que surgem em muitas aplicações.
Matemática discreta

A matemática discreta, em termos gerais, é o estudo de objetos matemáticos individuais e contáveis.[47] Como os objetos de estudo aqui são discretos, os métodos de cálculo e análise matemática não se aplicam diretamente.[d] Algoritmos — especialmente sua implementação e complexidade computacional — desempenham um papel importante na matemática discreta.[48]
O teorema das quatro cores e a conjectura de Kepler foram dois grandes problemas da matemática discreta resolvidos na segunda metade do século XX.[49] O problema P versus NP, que permanece não solucionado até os dias atuais, também é importante para a matemática discreta, uma vez que sua solução impactaria potencialmente um grande número de problemas computacionalmente difíceis.[50]
A matemática discreta inclui:[24]
- Combinatória, a arte de enumerar objetos matemáticos que satisfazem algumas restrições. Originalmente, estes objetos eram elementos ou subconjuntos de um determinado conjunto; isto foi estendido a vários objetos, o que estabelece uma forte ligação entre a combinatória e outras partes da matemática discreta. Por exemplo, a geometria discreta inclui a contagem de configurações de formas geométricas;
- Teoria dos grafos e hipergrafos;
- Teoria da codificação, incluindo códigos de correção de erros e uma parte da criptografia;
- Teoria matróide;
- Geometria discreta;
- Distribuições de probabilidade discretas;
- Teoria dos jogos (embora os jogos contínuos também sejam estudados, os jogos mais comuns, como xadrez e pôquer, são discretos);
- Otimização discreta, incluindo otimização combinatória, programação inteira, programação com restrições.
Lógica matemática e teoria dos conjuntos
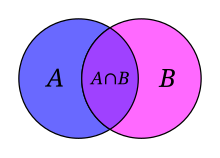
A disciplinas de lógica matemática e teoria dos conjuntos pertencem à matemática desde o final do século XIX.[51][52] Antes deste período, os conjuntos não eram considerados objetos matemáticos, e a lógica, embora usada em provas matemáticas, pertencia à filosofia e não era estudada especificamente pelos matemáticos.[53]
Antes do estudo de Cantor sobre conjuntos infinitos, os matemáticos relutavam em considerar coleções realmente infinitas e consideravam o infinito o resultado de uma enumeração infinita. O trabalho de Cantor ofendeu muitos matemáticos não apenas por considerar conjuntos realmente infinitos,[54] mas por mostrar que isto implica em diferentes tamanhos de infinito, de acordo com o argumento de diagonalização de Cantor.[55] Esta se tornou a crise fundamental da matemática.[56] Posteriormente, este problema foi resolvido na matemática convencional, ao sistematizar o método axiomático dentro de uma teoria de conjuntos formalizada. A grosso modo, cada objeto matemático é definido pelo conjunto de todos os objetos semelhantes e pelas propriedades que esses objetos devem ter.[22] Por exemplo, na aritmética de Peano, os números naturais são definidos por "zero é um número", "cada número tem um sucessor único", "cada número exceto zero tem um antecessor único" e algumas regras de raciocínio.[57] Esta abstração matemática da realidade está incorporada na filosofia moderna do formalismo, fundada por David Hilbert por volta de 1910.[58]
A "natureza" dos objetos definidos desta forma é um problema filosófico que os matemáticos deixam para os filósofos, mesmo que muitos matemáticos tenham opiniões— por vezes chamada de "intuições" — sobre isto e as usem para orientar o seu estudo e provas. A abordagem permite considerar "lógicas" (isto é, conjuntos de regras de dedução permitidas), teoremas, provas, etc, como objetos matemáticos e, assim, provar teoremas sobre eles. Por exemplo, os teoremas da incompletude de Gödel afirmam, a grosso modo, que, em todo sistema formal consistente que contém os números naturais, existem teoremas que são verdadeiros (que são demonstráveis num sistema mais forte), mas não demonstráveis dentro do sistema.[59] Esta abordagem aos fundamentos da matemática foi desafiada durante a primeira metade do século XX por matemáticos liderados por Brouwer, que promoveram a lógica intuicionista, que carece explicitamente da lei do terceiro excluído.[60][61] Estes problemas e debates acadêmicos levaram a uma ampla expansão da abrangência da lógica matemática, com o surgimento de subáreas como teoria dos modelos (modelagem de algumas teorias lógicas dentro de outras teorias), teoria da prova, teoria dos tipos, teoria da computabilidade e teoria da complexidade computacional.[24] Embora estes aspectos da lógica matemática tenham sido introduzidos antes do surgimento dos computadores, a sua utilização no design de compiladores, certificação de programas e outros aspectos da ciência da computação, contribuíram para a expansão destas teorias lógicas.[62]
Estatísticas e outras ciências de decisão
Algo se torna objetivo (em oposição a "subjetivo") assim que estamos convencidos de que existe nas mentes dos outros da mesma forma que existe nas nossas e que podemos pensar sobre isso e discuti-lo juntos.[63] Como a linguagem da matemática é tão precisa, ela é ideal para definir conceitos para os quais existe tal consenso. Na minha opinião, isso é suficiente para nos fornecer um sentimento de uma existência objetiva, de uma realidade matemática...

O campo de estudo da estatística é uma aplicação matemática empregada para a coleta e o processamento de amostras de dados, por meio do uso de procedimentos baseados em métodos matemáticos, especialmente a teoria das probabilidades. Os estatísticos geram dados com experimentos ou amostragem aleatória,[65] cujo desenho determina os métodos analíticos que serão utilizados. A análise dos dados de estudos observacionais é feita pela utilização de modelos estatísticos e da teoria da inferência, por meio de modelos de seleção e estimativa. Os modelos e as previsões consequentes devem então ser testados em relação a novos dados.[e]
A teoria estatística estuda problemas de decisão como a minimização do risco de uma ação estatística ao usar um procedimento, por exemplo, estimativa de parâmetros, teste de hipóteses e seleção de algoritimos. Nestas áreas tradicionais da estatística matemática, um problema de decisão estatística é formulado minimizando uma função de perda sob restrições específicas. Por exemplo, conceber uma pesquisa estatística frequentemente envolve minimizar o custo de estimar a média da população com alguma confiança.[66] Devido ao uso da otimização, a teoria estatística se sobrepõe a outras ciências da decisão, como a pesquisa operacional, a teoria do controle e a economia matemática.[67]
Matemática computacional
A matemática computacional é o estudo de problemas matemáticos que normalmente são grandes demais para a capacidade numérica dos seres humanos.[68][69] A análise numérica estuda métodos para problemas de análise utilizando a análise funcional e a teoria de aproximação; a análise numérica inclui o estudo de aproximação e discretização com foco especial em erros de arredondamento.[70]
História
Antiguidade


A história da matemática é uma série cada vez maior de abstrações. Evolutivamente falando, a primeira abstração a ser descoberta, compartilhada por muitos animais,[71] foi provavelmente a dos números: a constatação de que, por exemplo, uma coleção de duas maçãs e uma coleção de duas laranjas (digamos) têm algo em comum, nomeadamente que existem duas delas. Além de reconhecerem como contar objetos físicos, os povos pré-históricos também podem ter sabido contar quantidades abstratas, como o tempo — dias, estações ou anos.[72][73]
As primeiras evidências de matemática mais complexa só começam a aparecer por volta de 3.000 a.C., quando os povos babilônios e egípcios iniciam o uso de aritmética, álgebra e geometria para estimar seus impostos e fazer outros cálculos financeiros voltados para construção e astronomia.[74] Os textos matemáticos mais antigos da Mesopotâmia e do Egito datam de 2000 a.C. a 1800 a.C.. Muitos textos antigos mencionam triplos pitagóricos e assim, por inferência, o teorema de Pitágoras parece ser o conceito matemático mais antigo e difundido depois da aritmética e geometria básicas. É na matemática babilônica que a aritmética elementar (adição, subtração, multiplicação e divisão) aparece pela primeira vez no registro arqueológico. Os babilônios também possuíam um sistema de valor posicional e usavam um sistema de numeração sexagesimal que ainda é usado atualmente para medir ângulos e o tempo.[75]
No século VI a.C., a matemática grega começou a emergir como uma disciplina distinta e alguns gregos antigos, como os pitagóricos, pareciam tê-la considerado um assunto por direito próprio.[76] Por volta do ano 300 a.C., Euclides organizou o conhecimento matemático por meio de postulados e primeiros princípios, que evoluíram para o método axiomático usado atualmente na matemática, que consiste em definição, axioma, teorema e prova matemáticas.[77] Sua obra, Os Elementos, é amplamente considerada o livro didático de maior sucesso e influência de todos os tempos.[78] O maior matemático da antiguidade é frequentemente considerado Arquimedes (c. 287) de Siracusa.[79] Ele desenvolveu fórmulas para calcular a área superficial e o volume de sólidos de revolução e usou o método da exaustão para calcular a área sob o arco de uma parábola com a soma de uma série infinita, de uma maneira não muito diferente do cálculo moderno.[80] Outras conquistas notáveis da matemática grega são seções cônicas (Apolônio de Perga, século III a.C.),[81] trigonometria (Hiparco de Nicéia, século II a.C.)[82] e os primórdios da álgebra (Diofanto, século III d.C.).[83]

O sistema de numeração hindu-arábico e as regras para o uso de suas operações, em uso atualmente em todo o planeta, evoluíram no decorrer do primeiro milênio na Índia e foram transmitidos ao mundo ocidental através da matemática islâmica.[84] Outros desenvolvimentos notáveis da matemática indiana incluem a moderna definição e aproximação de seno e cosseno, além de uma forma inicial de séries infinitas.[85][86]
Medieval e posterior

Durante a Idade de Ouro Islâmica, especialmente durante os séculos IX e X, a matemática islâmica desenvolveu várias inovações importantes baseadas na matemática grega. A conquista mais notável da matemática islâmica foi o desenvolvimento da álgebra. Outras conquistas do período islâmico incluem avanços na trigonometria esférica e a adição do ponto decimal ao sistema de numeração arábico.[87] Muitos matemáticos notáveis deste período eram persas, como Alcuarismi, Omar Caiam e Xarafadim de Tus.[88] Os textos matemáticos gregos e árabes foram, por sua vez, traduzidos para o latim durante a Idade Média e reintroduzidos na Europa. [89]
No início da Idade Moderna, a matemática começou a desenvolver-se em ritmo acelerado na Europa Ocidental, com inovações revolucionárias, como a introdução de variáveis e da notação simbólica pelo francês François Viète (1540–1603), a introdução de logaritmos pelo escocês John Napier em 1614, que simplificou bastante os cálculos numéricos, especialmente para astronomia e navegação marítima, a introdução de coordenadas pelo francês René Descartes (1596-1650) para reduzir a geometria à álgebra, além do desenvolvimento do cálculo pelo inglês Isaac Newton (1642-1726/27) e pelo alemão Gottfried Leibniz (1646–1716). O suíço Leonhard Euler (1707-1783), o mais notável matemático do século XVIII, unificou todas estas inovações com uma terminologia padronizada e completou-as com a descoberta e a prova de vários teoremas.[90]

Talvez o principal matemático do século XIX tenha sido o alemão Carl Gauss, conhecido por ter feito inúmeras contribuições nos mais variados campos, como álgebra, análise, geometria diferencial, teoria das matrizes, teoria dos números e estatística.[91] Já no início do século XX, o austríaco Kurt Gödel transformou a matemática ao publicar os seus teoremas da incompletude, que mostram em parte que qualquer sistema axiomático consistente — se for suficientemente poderoso para descrever a aritmética — conterá proposições verdadeiras que não podem ser provadas.[59]
Desde então, a matemática foi bastante ampliada e tem havido uma interação frutífera com as ciências, com benefícios para ambas. Descobertas matemáticas continuam a ser feitas até os dias atuais. Por exemplo, de acordo com a edição de janeiro de 2006 do Bulletin of the American Mathematical Society: "O número de artigos e livros incluídos no banco de dados da Mathematical Reviews desde 1940 (o primeiro ano de operação da MR) é agora superior a 1,9 milhão e mais de 75 mil itens são adicionados ao banco de dados anualmente. A esmagadora maioria dos trabalhos neste oceano contém novos teoremas matemáticos e suas provas."[92]
Notação simbólica e terminologia

A notação matemática é amplamente utilizada na ciência e na engenharia para representar conceitos e propriedades complexas de forma concisa, inequívoca e precisa. Esta notação consiste em símbolos usados para representar operações, números não especificados, relações e quaisquer outros objetos matemáticos, e depois montá-los em expressões e fórmulas.[93] Mais precisamente, os números e outros objetos matemáticos são representados por símbolos chamados variáveis, que geralmente são letras latinas ou gregas. Operação e relações são geralmente representadas por símbolos ou glifos específicos,[94] como + (mais), × (multiplicação), (integral), = (igual) e < (menor que).[95] Todos esses símbolos são geralmente agrupados de acordo com regras específicas.[96]
A matemática desenvolveu uma terminologia rica que cobre uma ampla variedade de campos que estudam as propriedades de vários objetos e suas interações, sendo que fornecem uma base padrão para a comunicação. Um axioma ou postulado, por exemplo, é uma afirmação matemática considerada verdadeira sem necessidade de prova. Se uma afirmação matemática ainda não foi provada (ou refutada), ela é chamada de conjectura. Através de uma série de argumentos rigorosos empregando raciocínio dedutivo, uma afirmação que é comprovadamente verdadeira torna-se um teorema. Um teorema especializado usado principalmente para provar outro teorema é chamado de lema. Um exemplo comprovado que faz parte de uma conclusão mais geral é denominado corolário.[97]
Vários termos técnicos usados em matemática são neologismos, como polinômio e homeomorfismo.[98] Outros termos técnicos são palavras da linguagem comum usadas com um significado preciso que pode diferir ligeiramente do seu significado comum. Por exemplo, em matemática, "ou" significa "um, o outro ou ambos", enquanto, na linguagem comum, é ambíguo ou significa "um ou outro, mas não ambos" (em matemática, o último é chamado de "ou exclusivo"). Muitos termos matemáticos são palavras comuns usadas com um significado completamente diferente.[99]
Relação com as ciências
A matemática é usada na maioria das ciências para modelar fenômenos, o que permite que previsões sejam feitas a partir de leis experimentais.[100] A independência da matemática de qualquer experimentação implica que a precisão de tais previsões depende apenas da adequação do modelo.[101] No caso de previsões imprecisas, ao invés delas serem causadas por conceitos matemáticos inválidos, na verdade implicam na necessidade de alteração do modelo utilizado.[102] Por exemplo, a precessão do periélio do planeta Mercúrio só pôde ser explicada após o desenvolvimento da relatividade geral do alemão Albert Einstein, que substituiu a lei da gravitação universal do inglês Isaac Newton como um modelo matemático melhor.[103]
Atualmente, ainda há um debate filosófico sobre se a matemática pode ser classificada como uma ciência. No entanto, na prática, os matemáticos são normalmente considerados cientistas e a matemática tem muito em comum com as ciências físicas, já que é falsificável como elas, o que significa em que, se um resultado ou uma teoria estiverem errados, isto pode ser provado por meio da apresentação de um contraexemplo. Da mesma forma que na ciência, as teorias e os resultados matemáticos (teoremas) são frequentemente obtidos a partir da experimentação,[104] que pode consistir na computação de exemplos selecionados ou no estudo de figuras ou de outras representações de objetos matemáticos (muitas vezes representações mentais sem suporte físico). Por exemplo, quando questionado sobre como conseguiu seus teoremas, Gauss certa vez respondeu "durch planmässiges Tattonieren" ("através de experimentação sistemática").[105] Contudo, alguns autores enfatizam que a matemática difere da noção moderna de ciência por não se basear em evidências empíricas.[106][107][108][109]
Matemática pura e aplicada
Até ao século XIX, o desenvolvimento da matemática no mundo ocidental era motivado principalmente pelas necessidades trazidas pela tecnologia e ciência, sendo que não havia uma distinção clara entre matemática pura e aplicada.[110] Por exemplo, os números naturais e a aritmética foram introduzidos pela necessidade de contagem, enquanto a geometria foi motivada pela topografia, arquitetura e astronomia. Mais tarde, Isaac Newton introduziu o conceito do cálculo infinitesimal para explicar o movimento dos planetas com sua lei da gravitação universal. Além disso, a maioria dos matemáticos eram cientistas e muitos cientistas também eram matemáticos.[111] Contudo, uma exceção notável ocorreu com a tradição da matemática pura na Grécia Antiga.[112] O problema da fatoração de inteiros, por exemplo, que remonta a Euclides em 300 a.C., não tinha aplicação prática antes de seu uso no criptossistema RSA, que atualmente é amplamente utilizado para a segurança de redes de computadores.[113] No século XIX, matemáticos como os alemães Karl Weierstrass e Richard Dedekind concentraram cada vez mais as suas pesquisas em problemas internos, ou seja, na chamada matemática pura.[110][114] Isto levou à divisão da matemática em matemáticas pura e aplicada, sendo a última geralmente considerada de menor valor entre os puristas matemáticos. No entanto, a linha que diferencia as duas é tênue.[115]
As consequências da Segunda Guerra Mundial levou a um aumento no desenvolvimento da matemática aplicada nos Estados Unidos e em outros lugares.[116][117] Muitas das teorias desenvolvidas para aplicações foram consideradas interessantes do ponto de vista da matemática pura e muitos resultados da matemática pura demonstraram ter aplicações fora da matemática; por sua vez, o estudo destas aplicações poderá fornecer novos desenvolvimentos sobre a “teoria pura”.[118][119] Um exemplo do primeiro caso é a teoria das distribuições, introduzida por Laurent Schwartz para validar cálculos feitos em mecânica quântica, que se tornou imediatamente uma importante ferramenta de análise matemática (pura).[120] Um exemplo do segundo caso é a decidibilidade da teoria de primeira ordem dos números reais, um problema de matemática pura que foi provado verdadeiro por Alfred Tarski, com um algoritmo impossível de implementar devido a uma complexidade computacional bastante elevada.[121] Para obter um algoritmo que possa ser implementado e possa resolver sistemas de equações e desigualdades polinomiais, o matemática estadunidense George Collins introduziu a decomposição algébrica cilíndrica que se tornou uma ferramenta fundamental na geometria algébrica real.[122] Nos dias atuais, a distinção entre matemática pura e aplicada é mais uma questão de objetivo de pesquisa do que uma divisão da matemática em áreas amplas.[123][124] A Classificação de Disciplinas de Matemática, por exemplo, tem uma seção para "matemática geral aplicada", mas não menciona "matemática pura".[24]
Eficácia irracional
A eficácia irracional da matemática é um fenômeno que foi nomeado e explicitado pela primeira vez pelo físico Eugene Wigner[6] e descreve o fato de que muitas teorias matemáticas (mesmo as mais “puras”) têm aplicações fora do seu objeto inicial. Estas aplicações podem estar completamente fora da sua área inicial e podem dizer respeito a fenômenos físicos que eram completamente desconhecidos quando a teoria matemática foi introduzida.[125] Um exemplo notável é a fatoração primária de números naturais que foi descoberta mais de 2 mil anos antes de seu uso comum para comunicações seguras na Internet através do sistema criptográfico RSA.[126] Um segundo exemplo histórico é a teoria das elipses. Elas foram estudadas pelos antigos matemáticos gregos como seções cônicas (isto é, interseções de cones com planos). Quase 2 mil anos depois, Johannes Kepler descobriu que as trajetórias dos planetas são elipses.[127]
Durante o século XIX, o desenvolvimento interno da geometria (ou matemática pura) levou à definição e ao estudo de geometrias não euclidianas, espaços de dimensão superior a três e variedades. Neste período, estes conceitos pareciam totalmente desligados da realidade física. No início do século XX, no entanto, o alemão Albert Einstein desenvolveu a teoria da relatividade que utiliza fundamentalmente estes conceitos, principalmente o espaço-tempo da relatividade restrita é um espaço não euclidiano de dimensão quatro, enquanto o espaço-tempo da relatividade geral é uma variedade (curva) de dimensão quatro.[128][129]
Um aspecto marcante da interação entre matemática e física é quando a matemática impulsiona a pesquisa em física, o que é exemplificado pelas descobertas do pósitron e do bárion . Em ambos os casos, as equações das teorias apresentavam soluções inexplicáveis, o que levou à conjectura da existência de uma partícula desconhecida. Em ambos os casos, estas partículas foram descobertas alguns anos depois através de experiências específicas.[130][131][132]
Ciências específicas
Física

A matemática e a física influenciaram-se mutuamente ao longo da história moderna. A física moderna utliza amplamente a matemática[133] e é também a motivação por trás de grandes desenvolvimentos na matemática.[134]
Informática
A ascensão da tecnologia no século XX abriu caminho para uma nova ciência: a computação.[f] Este campo está intimamente relacionado à matemática de várias maneiras. A ciência da computação teórica, por exemplo, é essencialmente de natureza matemática. Em contrapartida, a informática também se tornou essencial para a obtenção de novos resultados. Este é um grupo de técnicas conhecidas como matemática experimental.[135] O exemplo mais conhecido é o teorema das quatro cores, comprovado em 1976 com a ajuda de um computador. Isto revolucionou a matemática tradicional, onde a regra até então era que o matemático verificasse cada parte da prova. Em 1998, a conjectura de Kepler sobre empacotamento de esferas também parecia ter sido parcialmente comprovada por um computador. Desde então, uma equipe internacional trabalhou na redação de uma prova formal, que foi concluída (e verificada) em 2015.[136] Um grande problema em aberto na ciência da computação teórica é P versus NP, um dos sete Problemas do Prêmio Millennium.[137]
Biologia

A biologia utiliza extensivamente a probabilidade, como por exemplo na ecologia ou na neurobiologia.[138] A maior parte do debate sobre probabilidade em biologia, entretanto, centra-se no conceito de aptidão evolutiva.[138]
A ecologia usa amplamente a modelagem para simular a dinâmica populacional,[138][139] estudar ecossistemas como o modelo predador-presa, medir a difusão da poluição,[140] ou para avaliar as mudanças climáticas.[141] A dinâmica de uma população pode ser modelada por equações diferenciais acopladas, como as equações de Lotka-Volterra.[142] No entanto, existe o problema da validação do modelo. Isto é particularmente grave quando os resultados da modelização influenciam as decisões políticas; a existência de modelos contraditórios poderia permitir às nações escolher o modelo mais favorável.[143]
Ciências sociais
As áreas da matemática utilizadas nas ciências sociais incluem probabilidade/estatística e equações diferenciais, que são usadas em linguística, economia, sociologia[144] e psicologia.[145]

O postulado fundamental da economia matemática é o do ator individual racional – Homo economicus (lit. "homem econômico").[146] Neste modelo, o indivíduo busca maximizar seu interesse próprio[146] e sempre faz escolhas ótimas usando informações perfeitas.[147] Contudo, muitas pessoas rejeitaram ou criticaram o conceito.[147] Economistas observam que pessoas reais têm informações limitadas, fazem escolhas erradas e se preocupam com a justiça, o altruísmo e não apenas com o ganho pessoal.[147]
No início do século XX, houve um desenvolvimento no sentido de expressar movimentos históricos através de fórmulas. Por exemplo, em 1922, Nikolai Kondratiev discerniu o ciclo Kondratiev de aproximadamente 50 anos, que explica fases de crescimento ou de crise econômica.[148] No final do século XIX, Nicolas-Remi Brück e Charles Henri Lagrange estenderam suas análises à geopolítica.[149] Desde a década de 1990, o antropólogo evolucionário russo-americano,Peter Turchin trabalha no desenvolvimento da cliodinâmica.[150]
Mesmo assim, a matematização das ciências sociais não é isenta de perigos. No polêmico livro Imposturas Intelectuais (1997), Sokal e Bricmont denunciaram o uso infundado ou abusivo de terminologia científica, especialmente da matemática ou da física, nas ciências sociais.[151]
Relação com astrologia e esoterismo
Alguns matemáticos renomados também foram considerados astrólogos renomados; por exemplo, Ptolomeu, astrônomos árabes, Regiomontano, Cardano, Kepler, ou John Dee. Na Idade Média, a astrologia era considerada uma ciência que incluía a matemática. Em sua enciclopédia, o físico suíço Theodor Zwinger escreveu que a astrologia era uma ciência matemática que estudava o "movimento ativo dos corpos à medida que agem sobre outros corpos" e reservou à matemática a necessidade de “calcular com probabilidade as influências [das estrelas]” para prever suas “conjunções e oposições”.[152] Atualmente, no entanto, a astrologia não é mais considerada uma ciência, mas sim uma pseudociência.[153]
Filosofia
Realidade
O matemático suíço Armand Borel resumiu esta visão da realidade matemática da seguinte forma, e forneceu citações de G. H. Hardy, Charles Hermite, Henri Poincaré e Albert Einstein que apoiam seus pontos de vista.[130] Entretanto, o platonismo e as visões concorrentes sobre a abstração não explicam necessariamente a eficácia irracional da matemática.[154]
Definições propostas
Não existe um consenso geral sobre uma definição de matemática ou o seu estatuto epistemológico — isto é, o seu lugar entre outras atividades humanas.[155][156] Muitos matemáticos profissionais não têm interesse em uma definição ou consideram a matemática como algo indefinível.[155] Sequer há consenso sobre se a matemática pode ser considerada uma arte ou uma ciência.[156] Alguns estudiosos apenas dizem que a “matemática é o que os matemáticos fazem”.[155] Isto faz sentido, pois existe um forte consenso entre eles sobre o que a matemática é e não é. A maioria das definições propostas tenta definir a matemática pelo seu objeto de estudo.[157]
Aristóteles definiu a matemática como “a ciência da quantidade” e esta definição prevaleceu até o século XVIII. No entanto, ele também observou que o foco apenas na quantidade pode não distinguir a matemática de ciências como a física; em sua opinião, a abstração e o estudo da quantidade como uma propriedade "separável no pensamento" das instâncias reais diferenciam a matemática.[158] No século XIX, quando os matemáticos começaram a abordar temas que não têm uma relação clara com a realidade física, como os conjuntos infinitos, foram dadas uma variedade de novas definições.[159]
Outra abordagem para definir matemática é fazer uso de seus métodos. Assim, uma área de estudo pode ser qualificada como matemática desde que possa provar teoremas, ou seja, afirmações cuja validade depende de uma prova, isto é, de uma dedução puramente lógica.[160] Outros, no entanto, assumem a perspectiva de que a matemática é uma investigação da teoria axiomática dos conjuntos, já que este estudo é atualmente uma disciplina fundamental para grande parte da matemática moderna.[161]
Rigor
O raciocínio matemático requer rigor. Isso significa que as definições devem ser absolutamente inequívocas e as provas devem ser redutíveis a uma sucessão de aplicações de regras de inferência,[g] sem qualquer uso de evidência empírica e intuição.[h][162] O raciocínio rigoroso não é específico da matemática, mas o padrão de rigor é muito mais alto do que em outros campos de estudo. Apesar da concisão da matemática, provas rigorosas podem exigir centenas de páginas para serem expressas. O surgimento de provas assistidas por computador permitiu que os comprimentos das provas se expandissem ainda mais,[i][163] como o teorema de Feit-Thompson de 255 páginas.[j] O resultado desta tendência é uma filosofia da prova quase empirista, mas que não pode ser considerada infalível.[9]
O conceito de rigor na matemática remonta à Grécia Antiga, onde a sociedade incentivava o raciocínio lógico e dedutivo. No entanto, o rigor tenderia a desencorajar a exploração de novas abordagens, tais como números irracionais e conceitos de infinito. O método de demonstração de provas rigorosas foi aprimorado ao longo do século XVI através do uso de notação simbólica. Durante o século XVIII, a transição social permitiu que os matemáticos passassem a ganhar seu sustento através do ensino, o que levou a uma reflexão mais cuidadosa sobre os conceitos subjacentes à matemática e produziu abordagens mais rigorosas durante a transição de métodos geométricos para provas algébricas e depois aritméticas.[9]
No final do século XIX, parecia que as definições dos conceitos básicos da matemática não eram suficientemente precisas para evitar paradoxos (geometria não euclidiana e função de Weierstrass) e contradições (paradoxo de Russell), o que foi resolvido pela inclusão de axiomas nas regras de inferência apodítica das teorias matemáticas; a reintrodução do método axiomático iniciado pelos antigos gregos antigos.[9] "Rigor" não é mais um conceito relevante em matemática, pois uma prova ou é correta ou é errônea, sendo que uma "prova rigorosa" é simplesmente um pleonasmo. Onde um conceito especial de rigor é aceito é nos aspectos socializados de uma prova, onde pode ser comprovadamente refutado por outros matemáticos. Depois de uma prova ter sido aceita por muitos anos ou mesmo décadas, ela pode então ser considerada confiável.[164] No entanto, o conceito de “rigor” ainda pode continuar sendo útil para ensinar aos iniciantes o que é uma prova matemática.[165]
Treinamento e prática
Educação
A matemática tem uma capacidade evidente de cruzar fronteiras culturais e períodos de tempo. Como atividade humana, a prática da matemática tem um aspecto social, que inclui educação, profissão, reconhecimento, popularização e assim por diante. Na educação, a matemática é uma parte central do currículo e constitui um elemento importante das disciplinas acadêmicas do grupo STEM. Carreiras proeminentes para matemáticos profissionais incluem professor de matemática, estatístico, atuário, analista financeiro, economista, contador, consultor de informática, entre outras.[166]
Evidências arqueológicas mostram que o ensino da matemática ocorreu já no segundo milênio a.C., na antiga Babilônia.[167] Evidências comparáveis foram descobertas nos escribas no Antigo Oriente Próximo e depois no mundo greco-romano, começando por volta do ano 300 a.C..[168] O livro didático de matemática mais antigo conhecido é o Papiro de Rhind, datado de c. 1650 a.C. no Egito Antigo.[169] Devido à escassez de livros, os ensinamentos matemáticos na Índia Antiga foram repassados através da tradição oral memorizada desde o período védico (c. 1500-500 a.C.).[170] Na China Imperial, durante a dinastia Tang (618-907 d.C.), um currículo de matemática foi adotado para concursos públicos para ingressar na burocracia estatal.[171]
Após a Idade das Trevas, a educação matemática na Europa era ministrada por escolas religiosas como parte do Quadrívio. A instrução formal em pedagogia começou nas escolas jesuítas ao longo dos séculos XVI e XVII. A maior parte do currículo matemático, no entanto, permaneceu em um nível básico e prático até o século XIX, quando começou a florescer na França e na Alemanha. O periódico mais antigo abordando o ensino de matemática foi L'Enseignement Mathématique, que começou a ser publicado no ano de 1899.[172] Os avanços do mundo ocidental na ciência e na tecnologia levaram ao estabelecimento de sistemas educativos centralizados em muitos Estados-nação, sendo a matemática um componente central — inicialmente por conta das suas aplicações militares.[173] Embora o conteúdo dos cursos varie, atualmente quase todos os países ensinam matemática aos seus alunos.[174]
Durante a escola, as capacidades matemáticas e as expectativas positivas têm uma forte associação com o interesse profissional na área. Fatores extrínsecos, como apoio de professores, pais e grupos de pares, podem influenciar o nível de interesse pela matemática.[175] Alguns alunos que estudam matemática podem desenvolver apreensão ou medo em relação ao seu desempenho na matéria, o que é conhecido como ansiedade matemática ou fobia matemática e é considerado o mais proeminente dos distúrbios que afetam o desempenho acadêmico. Isto pode se desenvolver devido a vários fatores, como atitudes dos pais e professores, estereótipos sociais e características pessoais. A ajuda para neutralizar este problema pode advir de mudanças nas abordagens instrucionais, de interações com pais e professores e de tratamentos personalizados para cada estudante.[176]
Psicologia (estética, criatividade e intuição)
A validade de um teorema matemático depende apenas do rigor da sua prova, que teoricamente poderia ser feita automaticamente por um programa de computador. Isto não significa que não há lugar para criatividade num trabalho matemático. Pelo contrário, muitos resultados matemáticos importantes (teoremas) são soluções de problemas que outros matemáticos não conseguiram resolver e a invenção de uma forma de resolução pode ser uma forma fundamental do processo de resolução.[177][178] Um exemplo extremo é o teorema de Roger Apéry, cujo autor forneceu apenas as ideias para uma prova e a prova formal foi dada apenas alguns meses depois por três outros matemáticos.[179]
A criatividade e o rigor não são os únicos aspectos psicológicos da atividade dos matemáticos. Alguns deles podem ver a sua atividade como um jogo. Este aspecto da atividade matemática é enfatizado na matemática recreativa.[180] Os matemáticos podem encontrar um valor estético para o seu campo de estudo. Assim como a beleza, a matemática é difícil de definir, está comumente relacionada à elegância, que envolve qualidades como simplicidade, simetria, completude e generalidade. G. H. Hardy, em sua obra Apologia do Matemático, expressou a crença de que as considerações estéticas são, em si, suficientes para justificar o estudo da matemática pura. Ele também identificou outros critérios, como significância, imprevisibilidade e inevitabilidade, que contribuem para a estética matemática.[181] Paul Erdős expressou este sentimento de forma mais irônica ao falar de "O Livro", uma suposta coleção divina das mais belas provas. A obra literária Provas conforme O Livro de 1998, inspirado no livro de Erdős, é uma coleção de argumentos matemáticos particularmente sucintos e reveladores. Alguns exemplos de resultados particularmente elegantes incluídos são a prova de Euclides de que existem infinitos números primos e a transformada rápida de Fourier para análise harmônica.[182]
Alguns acham que considerar a matemática uma ciência é subestimar a sua arte e história nas sete artes liberais tradicionais.[183] Uma forma desta diferença de ponto de vista se manifestar é no debate filosófico sobre se os resultados matemáticos são criados (como na arte) ou descobertos (como na ciência).[130]
Impacto cultural
Expressão artística

Notas musicais que soam bem juntas para um ouvido ocidental são sons cujas frequências fundamentais de vibração estão em proporções simples. Por exemplo, uma oitava duplica a frequência e uma quinta justa multiplica-a por .[184][185]
Os humanos, assim como alguns outros animais, consideram os padrões simétricos mais bonitos.[186] Matematicamente, as simetrias de um objeto formam um grupo conhecido como grupo de simetria.[187]
Por exemplo, o grupo subjacente à simetria do espelho é o grupo cíclico de dois elementos, . Um teste de Rorschach é uma figura invariante por esta simetria,[188] assim como os corpos de borboletas e animais em geral (pelo menos na superfície).[189] As ondas na superfície do mar possuem simetria de translação: mover o ponto de vista pela distância entre as cristas das ondas não altera a visão do mar. Fractais possuem autossimilaridade.[190][191]
Popularização
A matemática popular é o ato de apresentar a matemática sem termos técnicos.[192] Apresentar matemática pode ser difícil, uma vez que o público em geral sofre de ansiedade matemática e os objetos matemáticos são altamente abstratos.[193] No entanto, a escrita matemática popular pode superar isto usando aplicativos ou referências culturais.[194]
Prêmios

O prêmio de maior prestígio em matemática é a Medalha Fields,[195][196] criada em 1936 e concedida a cada quatro anos (exceto por volta da Segunda Guerra Mundial) a até quatro indivíduos.[197][198] É considerado o equivalente matemático do Prêmio Nobel.[198]
Outros prêmios de matemática de prestígio incluem:[199]
- O Prêmio Abel, instituído em 2002[200] e concedido pela primeira vez em 2003;[201]
- A Medalha Chern pelo conjunto da obra, introduzida em 2009[202] e concedida pela primeira vez em 2010;[203]
- O Prêmio AMS Leroy P. Steele, concedido desde 1970;[204]
- O Prêmio Wolf de Matemática, também pelo conjunto da obra,[205] instituído em 1978.[206]
Uma famosa lista de 23 problemas em aberto, chamada "problemas de Hilbert", foi compilada em 1900 pelo matemático alemão David Hilbert.[207] Esta lista alcançou grande celebridade entre os matemáticos[208] e, desde 2022, pelo menos treze dos problemas (dependendo de como alguns são interpretados) foram resolvidos.[207]
Uma nova lista de sete problemas importantes, intitulada "Problemas do Prêmio Millennium", foi publicada no ano 2000. Apenas uma delas, a Hipótese de Riemann, duplica um dos problemas de Hilbert. Uma solução para qualquer um desres problemas acarreta uma recompensa de 1 milhão de dólares.[209] Até hoje, apenas um destes problemas, a Conjectura de Poincaré, foi resolvido.[210]
Ver também
Notas e referências
Notas
- ↑ Aqui, álgebra é tomada em seu sentido moderno, que é, grosso modo, a arte de manipular fórmulas.
- ↑ Este significado pode ser encontrado na obra República de Platão, Livro 6, Seção 510c.[11] No entanto, Platão não usou uma palavra “matemática”; Aristóteles fez isto, comentando sobre isso.[12][13]
- ↑ Isso inclui seções cônicass, que são interseções de cilindros circulares e planos.
- ↑ No entanto, alguns métodos avançados de análise são por vezes utilizados; por exemplo, métodos de análise complexa aplicados à função geradora.
- ↑ Como outras ciências matemáticas, como física e ciência da computação, a estatística é uma disciplina autônoma e não um ramo da matemática aplicada. Assim como os físicos pesquisadores e os cientistas da computação, os estatísticos pesquisadores são cientistas matemáticos. Muitos estatísticos são formados em matemática e alguns estatísticos também são matemáticos.
- ↑ Ada Lovelace é conhecida por ter escrito, na década de 1840, o primeiro programa de computador em colaboração com Charles Babbage
- ↑ Isto não significa tornar explícitas todas as regras de inferência utilizadas. Pelo contrário, isto geralmente é impossível, sem computadores e assistentes de prova. Mesmo com esta tecnologia moderna, podem ser necessários anos de trabalho humano para redigir uma prova matemática completamente detalhada.
- ↑ Isto não significa que a evidência empírica e a intuição não sejam necessárias para escolher os teoremas a provar e para os provar.
- ↑ Para considerar como confiável um grande cálculo que ocorre em uma prova, geralmente são necessários dois cálculos usando um software independente
- ↑ O livro que contém a prova completa tem mais de mil páginas.
Referências
- ↑ a b «Mathematics (noun)». Oxford English Dictionary. Oxford University Press. Consultado em 17 de janeiro de 2024
- ↑ Kneebone, G. T. (1963). «Traditional Logic». Mathematical Logic and the Foundations of Mathematics: An Introductory Survey. [S.l.]: D. Van Nostard Company. LCCN 62019535. MR 0150021. OCLC 792731
- ↑ LaTorre, Donald R.; Kenelly, John W.; Reed, Iris B.; Carpenter, Laurel R.; Harris, Cynthia R.; Biggers (2008). «Models and Functions». Calculus Concepts: An Applied Approach to the Mathematics of Change 4th ed. [S.l.]: Houghton Mifflin Company. ISBN 978-0-618-78983-2. LCCN 2006935429. OCLC 125397884
- ↑ Hipólito, Inês Viegas (15 de agosto de 2015). «Abstract Cognition and the Nature of Mathematical Proof». In: Kanzian; Mitterer; Neges. Realismus – Relativismus – Konstruktivismus: Beiträge des 38. Internationalen Wittgenstein Symposiums (PDF) (em alemão e inglês). 23. Kirchberg am Wechsel, Austria: Austrian Ludwig Wittgenstein Society. pp. 132–134. ISSN 1022-3398. OCLC 236026294. Consultado em 17 de janeiro de 2024. Cópia arquivada (PDF) em 7 de novembro de 2022 (at ResearchGate
 Arquivado em 2022-11-05 no Wayback Machine)
Arquivado em 2022-11-05 no Wayback Machine)
- ↑ Peterson 1988, p. 12.
- ↑ a b Wigner, Eugene (1960). «The Unreasonable Effectiveness of Mathematics in the Natural Sciences». Communications on Pure and Applied Mathematics. 13 (1): 1–14. Bibcode:1960CPAM...13....1W. doi:10.1002/cpa.3160130102. Cópia arquivada em 28 de fevereiro de 2011
- ↑ Wise, David. «Eudoxus' Influence on Euclid's Elements with a close look at The Method of Exhaustion». Universidade da Geórgia. Consultado em 18 de janeiro de 2024. Arquivado do original em 1 de junho de 2019
- ↑ Alexander, Amir (setembro de 2011). «The Skeleton in the Closet: Should Historians of Science Care about the History of Mathematics?». Isis. 102 (3): 475–480. ISSN 0021-1753. MR 2884913. PMID 22073771. doi:10.1086/661620
- ↑ a b c d e f Kleiner, Israel (dezembro de 1991). «Rigor and Proof in Mathematics: A Historical Perspective». Taylor & Francis, Ltd. Mathematics Magazine. 64 (5): 291–314. ISSN 0025-570X. JSTOR 2690647. LCCN 47003192. MR 1141557. OCLC 1756877. doi:10.1080/0025570X.1991.11977625
- ↑ a b Harper, Douglas (28 de março de 2019). Mathematic (n.). Consultado em 25 de janeiro de 2024. Arquivado do original em 7 de março de 2013
- ↑ Plato. Republic, Book 6, Section 510c. [S.l.: s.n.] Consultado em 2 de fevereiro de 2024. Cópia arquivada em 24 de fevereiro de 2021
- ↑ Liddell, Henry George; Scott, Robert (1940). A Greek–English Lexicon. Clarendon Press
- ↑ Harper, Douglas (20 de abril de 2022). «Mathematics (n.)». Online Etymology Dictionary. Consultado em 2 de fevereiro de 2024
- ↑ Harper, Douglas (22 de dezembro de 2018). Mathematical (adj.). Consultado em 25 de janeiro de 2024. Arquivado do original em 26 de novembro de 2022
- ↑ Perisho, Margaret W. (1965). «The Etymology of Mathematical Terms». Pi Mu Epsilon Journal. 4 (2): 62–66. ISSN 0031-952X. JSTOR 24338341. LCCN 58015848. OCLC 1762376
- ↑ Boas, Ralph P. (1995). «What Augustine Didn't Say About Mathematicians». In: Alexanderson; Mugler, Dale H. Lion Hunting and Other Mathematical Pursuits: A Collection of Mathematics, Verse, and Stories. [S.l.]: Mathematical Association of America. ISBN 978-0-88385-323-8. LCCN 94078313. OCLC 633018890
- ↑ Bell, E. T. (1945). «General Prospectus». The Development of Mathematics 2nd ed. [S.l.]: Dover Publications. ISBN 978-0-486-27239-9. LCCN 45010599. OCLC 523284
- ↑ Tiwari, Sarju (1992). «A Mirror of Civilization». Mathematics in History, Culture, Philosophy, and Science 1st ed. Nova Deli: Mittal Publications. ISBN 978-81-7099-404-6. LCCN 92909575. OCLC 28115124
- ↑ Restivo, Sal (1992). «Mathematics from the Ground Up». In: Bunge, Mario. Mathematics in Society and History. Col: Episteme. 20. [S.l.]: Kluwer Academic Publishers. ISBN 0-7923-1765-3. LCCN 25709270. OCLC 92013695
- ↑ Musielak, Dora (2022). Leonhard Euler and the Foundations of Celestial Mechanics. Col: History of Physics. [S.l.]: Springer International Publishing. ISBN 978-3-031-12321-4. ISSN 2730-7549. OCLC 1332780664. doi:10.1007/978-3-031-12322-1
- ↑ Biggs, N. L. (Maio de 1979). «The roots of combinatorics». Historia Mathematica. 6 (2): 109–136. ISSN 0315-0860. LCCN 75642280. OCLC 2240703. doi:10.1016/0315-0860(79)90074-0

- ↑ a b Warner, Evan. «Splash Talk: The Foundational Crisis of Mathematics» (PDF). Universidade Columbia. Consultado em 3 de fevereiro de 2024. Arquivado do original (PDF) em 22 de março de 2023
- ↑ Dunne, Edward; Hulek, Klaus (Março de 2020). «Mathematics Subject Classification 2020» (PDF). Notices of the American Mathematical Society. 67 (3): 410–411. ISSN 0002-9920. LCCN sf77000404. OCLC 1480366. doi:10.1090/noti2052
 . Consultado em 3 de fevereiro de 2024. Cópia arquivada (PDF) em 3 de agosto de 2021
. Consultado em 3 de fevereiro de 2024. Cópia arquivada (PDF) em 3 de agosto de 2021
- ↑ a b c d e f g h «MSC2020-Mathematics Subject Classification System» (PDF). zbMath. Associate Editors of Mathematical Reviews and zbMATH. Consultado em 3 de fevereiro de 2024. Arquivado do original (PDF) em 2 de janeiro de 2024
- ↑ LeVeque, William J. (1977). «Introduction». Fundamentals of Number Theory. [S.l.]: Addison-Wesley Publishing Company. pp. 1–30. ISBN 0-201-04287-8. LCCN 76055645. OCLC 3519779
- ↑ Goldman, Jay R. (1998). «The Founding Fathers». The Queen of Mathematics: A Historically Motivated Guide to Number Theory. Wellesley, MA: A K Peters. pp. 2–3. ISBN 1-56881-006-7. LCCN 94020017. OCLC 30437959. doi:10.1201/9781439864623
- ↑ Weil, André (1983). Number Theory: An Approach Through History From Hammurapi to Legendre. [S.l.]: Birkhäuser Boston. pp. 2–3. ISBN 0-8176-3141-0. LCCN 83011857. OCLC 9576587. doi:10.1007/978-0-8176-4571-7
- ↑ Kleiner, Israel (março de 2000). «From Fermat to Wiles: Fermat's Last Theorem Becomes a Theorem». Elemente der Mathematik. 55 (1): 19–37. ISSN 0013-6018. LCCN 66083524. OCLC 1567783. doi:10.1007/PL00000079

- ↑ Wang, Yuan (2002). The Goldbach Conjecture. Col: Series in Pure Mathematics. 4 2nd ed. [S.l.]: World Scientific. pp. 1–18. ISBN 981-238-159-7. LCCN 2003268597. OCLC 51533750. doi:10.1142/5096
- ↑ a b c d Straume, Eldar (4 de setembro de 2014). «A Survey of the Development of Geometry up to 1870». arXiv:1409.1140
 [math.HO]
[math.HO]
- ↑ Hilbert, David (1902). The Foundations of Geometry. [S.l.]: Open Court Publishing Company. LCCN 02019303. OCLC 996838. doi:10.1126/science.16.399.307. Consultado em 6 de fevereiro de 2024

- ↑ Hartshorne, Robin (2000). «Euclid's Geometry». Geometry: Euclid and Beyond. [S.l.]: Springer New York. pp. 9–13. ISBN 0-387-98650-2. LCCN 99044789. OCLC 42290188. Consultado em 7 de fevereiro de 2024
- ↑ Boyer, Carl B. (2004). «Fermat and Descartes». History of Analytic Geometry. [S.l.]: Dover Publications. pp. 74–102. ISBN 0-486-43832-5. LCCN 2004056235. OCLC 56317813
- ↑ Stump, David J. (1997). «Reconstructing the Unity of Mathematics circa 1900» (PDF). Perspectives on Science. 5 (3): 383–417. ISSN 1063-6145. LCCN 94657506. OCLC 26085129. doi:10.1162/posc_a_00532. Consultado em 8 de fevereiro de 2024
- ↑ O'Connor, J. J.; Robertson, E. F. (Fevereiro de 1996). «Non-Euclidean geometry». Escócia. Universidade de St. Andrews. Consultado em 8 de fevereiro de 2024 [ligação inativa]
- ↑ Joyner, David (2008). «The (legal) Rubik's Cube group». Adventures in Group Theory: Rubik's Cube, Merlin's Machine, and Other Mathematical Toys 2nd ed. [S.l.]: Johns Hopkins University. pp. 219–232. ISBN 978-0-8018-9012-3. LCCN 2008011322. OCLC 213765703
- ↑ Christianidis, Jean; Oaks, Jeffrey (Maio de 2013). «Practicing algebra in late antiquity: The problem-solving of Diophantus of Alexandria». Historia Mathematica. 40 (2): 127–163. ISSN 0315-0860. LCCN 75642280. OCLC 2240703. doi:10.1016/j.hm.2012.09.001

- ↑ Kleiner 2007, "History of Classical Algebra" pp. 3–5.
- ↑ Lim, Lisa (21 de dezembro de 2018). «Where the x we use in algebra came from, and the X in Xmas». South China Morning Post. Consultado em 8 de fevereiro de 2024. Arquivado do original em 22 de dezembro de 2018
- ↑ Oaks, Jeffery A. (2018). «François Viète's revolution in algebra» (PDF). Archive for History of Exact Sciences. 72 (3): 245–302. ISSN 0003-9519. LCCN 63024699. OCLC 1482042. doi:10.1007/s00407-018-0208-0. Consultado em 8 de fevereiro de 2024. Cópia arquivada (PDF) em 8 de novembro de 2022
- ↑ Kleiner 2007, "History of Linear Algebra" pp. 79–101.
- ↑ Corry, Leo (2004). «Emmy Noether: Ideals and Structures». Modern Algebra and the Rise of Mathematical Structures 2ª revisada ed. Alemanha: Birkhäuser Basel. pp. 247–252. ISBN 3-7643-7002-5. LCCN 2004556211. OCLC 51234417. Consultado em 8 de fevereiro de 2024
- ↑ Riche, Jacques (2007). «From Universal Algebra to Universal Logic». In: Beziau; Costa-Leite. Perspectives on Universal Logic. Milano, Italy: Polimetrica International Scientific Publisher. pp. 3–39. ISBN 978-88-7699-077-9. OCLC 647049731. Consultado em 8 de fevereiro de 2024
- ↑ Krömer, Ralph (2007). Tool and Object: A History and Philosophy of Category Theory. Col: Science Networks - Historical Studies. 32. Alemanha: Springer Science & Business Media. pp. xxi–xxv, 1–91. ISBN 978-3-7643-7523-2. LCCN 2007920230. OCLC 85242858. Consultado em 8 de fevereiro de 2024
- ↑ Guicciardini, Niccolo (2017). «The Newton–Leibniz Calculus Controversy, 1708–1730». In: Schliesser; Smeenk. The Oxford Handbook of Newton (PDF). Col: Oxford Handbooks. [S.l.]: Oxford University Press. ISBN 978-0-19-993041-8. OCLC 975829354. doi:10.1093/oxfordhb/9780199930418.013.9. Consultado em 9 de fevereiro de 2024. Cópia arquivada (PDF) em 9 de novembro de 2022
- ↑ O'Connor, J. J.; Robertson, E. F. (Setembro de 1998). MacTutor, ed. «Leonhard Euler». Escócia. Universidade de St. Andrews. Consultado em 9 de fevereiro de 2024. Arquivado do original em 9 de novembro de 2022
- ↑ Franklin, James (Julho de 2017). «Discrete and Continuous: A Fundamental Dichotomy in Mathematics». Journal of Humanistic Mathematics. 7 (2): 355–378. ISSN 2159-8118. LCCN 2011202231. OCLC 700943261. doi:10.5642/jhummath.201702.18
 . Consultado em 9 de fevereiro de 2024
. Consultado em 9 de fevereiro de 2024
- ↑ Maurer, Stephen B. (1997). «What is Discrete Mathematics? The Many Answers». In: Rosenstein; Franzblau; Roberts. Discrete Mathematics in the Schools. Col: DIMACS: Series in Discrete Mathematics and Theoretical Computer Science. 36. [S.l.]: American Mathematical Society. pp. 121–124. ISBN 0-8218-0448-0. ISSN 1052-1798. LCCN 97023277. OCLC 37141146. doi:10.1090/dimacs/036/13
- ↑ Hales, Thomas C. (2014). «Turing's Legacy: Developments from Turing's Ideas in Logic». In: Downey, Rod. Turing's Legacy. Col: Lecture Notes in Logic. 42. [S.l.]: Cambridge University Press. pp. 260–261. ISBN 978-1-107-04348-0. LCCN 2014000240. OCLC 867717052. doi:10.1017/CBO9781107338579.001
- ↑ Sipser, Michael (Julho de 1992). The History and Status of the P versus NP Question. STOC '92: Proceedings of the twenty-fourth annual ACM symposium on Theory of Computing. pp. 603–618. doi:10.1145/129712.129771
- ↑ Ewald, William (17 de novembro de 2018). «The Emergence of First-Order Logic». Stanford Encyclopedia of Philosophy. Consultado em 2 de novembro de 2022. Arquivado do original em 12 de maio de 2021
- ↑ Ferreirós, José (18 de junho de 2020). «The Early Development of Set Theory». Stanford Encyclopedia of Philosophy. Consultado em 2 de novembro de 2022. Arquivado do original em 12 de maio de 2021
- ↑ Ferreirós, José (2001). «The Road to Modern Logic—An Interpretation» (PDF). Bulletin of Symbolic Logic. 7 (4): 441–484. JSTOR 2687794. doi:10.2307/2687794. Consultado em 11 de novembro de 2022. Cópia arquivada (PDF) em 2 de fevereiro de 2023
- ↑ Wolchover, Natalie (3 de dezembro de 2013). «Dispute over Infinity Divides Mathematicians». Scientific American. Consultado em 1 de novembro de 2022. Arquivado do original em 2 de novembro de 2022
- ↑ Zhuang, C. «Wittgenstein's analysis on Cantor's diagonal argument». PhilArchive. Consultado em 18 de novembro de 2022
- ↑ Avigad, Jeremy; Reck, Erich H. (11 de dezembro de 2001). «"Clarifying the nature of the infinite": the development of metamathematics and proof theory» (PDF). Carnegie Mellon Technical Report CMU-PHIL-120. Consultado em 12 de novembro de 2022. Arquivado do original (PDF) em 9 de outubro de 2022
- ↑ Hamilton, Alan G. (1982). Numbers, Sets and Axioms: The Apparatus of Mathematics. [S.l.]: Cambridge University Press. pp. 3–4. ISBN 978-0-521-28761-6. Consultado em 12 de novembro de 2022
- ↑ Snapper, Ernst (Setembro de 1979). «The Three Crises in Mathematics: Logicism, Intuitionism, and Formalism». Mathematics Magazine. 52 (4): 207–216. JSTOR 2689412. doi:10.2307/2689412
- ↑ a b Raatikainen, Panu (Outubro de 2005). «On the Philosophical Relevance of Gödel's Incompleteness Theorems». Revue Internationale de Philosophie. 59 (4): 513–534. JSTOR 23955909. doi:10.3917/rip.234.0513. Consultado em 12 de novembro de 2022. Cópia arquivada em 12 de novembro de 2022
- ↑ Moschovakis, Joan (4 de setembro de 2018). «Intuitionistic Logic». Stanford Encyclopedia of Philosophy. Consultado em 12 de novembro de 2022. Arquivado do original em 16 de dezembro de 2022
- ↑ McCarty, Charles (2006). «At the Heart of Analysis: Intuitionism and Philosophy». Philosophia Scientiæ, Cahier spécial 6: 81–94. doi:10.4000/philosophiascientiae.411

- ↑ Halpern, Joseph; Harper, Robert; Immerman, Neil; Kolaitis, Phokion; Vardi, Moshe; Vianu, Victor (2001). «On the Unusual Effectiveness of Logic in Computer Science» (PDF). Consultado em 15 de janeiro de 2021. Arquivado do original (PDF) em 3 de março de 2021
- ↑ Ver White, L. (1947). «The locus of mathematical reality: An anthropological footnote». Philosophy of Science. 14 (4): 289–303. doi:10.1086/286957. 189303; also in Newman, J. R. (1956). The World of Mathematics. 4. New York: Simon and Schuster. pp. 2348–2364
- ↑ Rouaud, Mathieu (Abril de 2017). Probability, Statistics and Estimation (PDF). [S.l.: s.n.] Consultado em 13 de fevereiro de 2024. Cópia arquivada (PDF) em 9 de outubro de 2022
- ↑ Rao, C. Radhakrishna (1997). Statistics and Truth: Putting Chance to Work 2nd ed. [S.l.]: World Scientific. pp. 3–17, 63–70. ISBN 981-02-3111-3. LCCN 97010349. MR 1474730. OCLC 36597731
- ↑ Rao, C. Radhakrishna (1981). «Foreword». In: Arthanari; Dodge. Mathematical programming in statistics. Col: Wiley Series in Probability and Mathematical Statistics. New York: Wiley. pp. vii–viii. ISBN 978-0-471-08073-2. LCCN 80021637. MR 607328. OCLC 6707805
- ↑ Whittle 1994, pp. 10–11, 14–18.
- ↑ Marchuk, Gurii Ivanovich (abril de 2020). «G I Marchuk's plenary: ICM 1970». School of Mathematics and Statistics, University of St Andrews, Scotland. Consultado em 13 de novembro de 2022. Arquivado do original em 13 de novembro de 2022
- ↑ Johnson, Gary M.; Cavallini, John S. (Setembro de 1991). Phua, Kang Hoh; Loe, Kia Fock, eds. Grand Challenges, High Performance Computing, and Computational Science. Singapore Supercomputing Conference'90: Supercomputing For Strategic Advantage. World Scientific. p. 28. LCCN 91018998. Consultado em 13 de novembro de 2022
- ↑ Trefethen, Lloyd N. (2008). «Numerical Analysis». In: Gowers, Timothy; Barrow-Green, June; Leader, Imre. The Princeton Companion to Mathematics (PDF). [S.l.]: Princeton University Press. pp. 604–615. ISBN 978-0-691-11880-2. LCCN 2008020450. MR 2467561. OCLC 227205932. Consultado em 15 de fevereiro de 2024. Cópia arquivada (PDF) em 7 de março de 2023
- ↑ Dehaene, Stanislas; Dehaene-Lambertz, Ghislaine; Cohen, Laurent (Agosto de 1998). «Abstract representations of numbers in the animal and human brain». Trends in Neurosciences. 21 (8): 355–361. PMID 9720604. doi:10.1016/S0166-2236(98)01263-6
- ↑ See, for example, Wilder, Raymond L. Evolution of Mathematical Concepts; an Elementary Study. [S.l.: s.n.]
- ↑ Zaslavsky, Claudia (1999). Africa Counts: Number and Pattern in African Culture. [S.l.]: Chicago Review Press. ISBN 978-1-61374-115-3. OCLC 843204342
- ↑ Kline 1990, Chapter 1.
- ↑ Boyer 1991, "Mesopotamia" pp. 24–27.
- ↑ Heath, Thomas Little (1981). A History of Greek Mathematics: From Thales to Euclid. New York: Dover Publications. ISBN 978-0-486-24073-2
- ↑ Mueller, I. (1969). «Euclid's Elements and the Axiomatic Method». The British Journal for the Philosophy of Science. 20 (4): 289–309. ISSN 0007-0882. JSTOR 686258. doi:10.1093/bjps/20.4.289
- ↑ Boyer 1991, "Euclid of Alexandria" p. 119.
- ↑ Boyer 1991, "Archimedes of Syracuse" p. 120.
- ↑ Boyer 1991, "Archimedes of Syracuse" p. 130.
- ↑ Boyer 1991, "Apollonius of Perga" p. 145.
- ↑ Boyer 1991, "Greek Trigonometry and Mensuration" p. 162.
- ↑ Boyer 1991, "Revival and Decline of Greek Mathematics" p. 180.
- ↑ Ore, Øystein (1988). Number Theory and Its History. [S.l.]: Courier Corporation. pp. 19–24. ISBN 978-0-486-65620-5. Consultado em 14 de novembro de 2022
- ↑ Singh, A. N. (Janeiro de 1936). «On the Use of Series in Hindu Mathematics». Osiris. 1: 606–628. JSTOR 301627. doi:10.1086/368443
- ↑ Kolachana, A.; Mahesh, K.; Ramasubramanian, K. (2019). «Use of series in India». Studies in Indian Mathematics and Astronomy. Col: Sources and Studies in the History of Mathematics and Physical Sciences. Singapore: Springer. pp. 438–461. ISBN 978-981-13-7325-1. doi:10.1007/978-981-13-7326-8_20
- ↑ Saliba, George (1994). A history of Arabic astronomy: planetary theories during the golden age of Islam. [S.l.]: New York University Press. ISBN 978-0-8147-7962-0. OCLC 28723059
- ↑ Faruqi, Yasmeen M. (2006). «Contributions of Islamic scholars to the scientific enterprise». Shannon Research Press. International Education Journal. 7 (4): 391–399. Consultado em 14 de novembro de 2022. Cópia arquivada em 14 de novembro de 2022
- ↑ Lorch, Richard (Junho de 2001). «Greek-Arabic-Latin: The Transmission of Mathematical Texts in the Middle Ages» (PDF). Cambridge University Press. Science in Context. 14 (1–2): 313–331. doi:10.1017/S0269889701000114. Consultado em 5 de dezembro de 2022. Cópia arquivada (PDF) em 17 de dezembro de 2022
- ↑ Finkel, B.F. (1897). «Biography- Leonard Euler». The American Mathematical Monthly. 4 (12). 300 páginas
- ↑ Archibald, Raymond Clare (Janeiro de 1949). «History of Mathematics After the Sixteenth Century». The American Mathematical Monthly. Part 2: Outline of the History of Mathematics. 56 (1): 35–56. JSTOR 2304570. doi:10.2307/2304570
- ↑ Sevryuk 2006, pp. 101–109.
- ↑ Wolfram, Stephan (outubro de 2000). Mathematical Notation: Past and Future. MathML and Math on the Web: MathML International Conference 2000, Urbana Champaign, USA. Consultado em 3 de fevereiro de 2024. Cópia arquivada em 16 de novembro de 2022
- ↑ Douglas, Heather; Headley, Marcia Gail; Hadden, Stephanie; LeFevre, Jo-Anne (3 de dezembro de 2020). «Knowledge of Mathematical Symbols Goes Beyond Numbers». Journal of Numerical Cognition. 6 (3): 322–354. doi:10.5964/jnc.v6i3.293

- ↑ Letourneau, Mary; Wright Sharp, Jennifer (outubro de 2017). «AMS Style Guide» (PDF). American Mathematical Society. p. 75. Consultado em 3 de fevereiro de 2024. Arquivado do original (PDF) em 8 de dezembro de 2022
- ↑ Jansen, Anthony R.; Marriott, Kim; Yelland, Greg W. (2000). «Constituent Structure in Mathematical Expressions» (PDF). Universidade da Califórnia em Merced. Proceedings of the Annual Meeting of the Cognitive Science Society. 22. OCLC 68713073. Consultado em 3 de fevereiro de 2024. Cópia arquivada (PDF) em 16 de novembro de 2022
- ↑ Rossi, Richard J. (2006). Theorems, Corollaries, Lemmas, and Methods of Proof. Col: Pure and Applied Mathematics: A Wiley Series of Texts, Monographs and Tracts. [S.l.]: John Wiley & Sons. pp. 1–14, 47–48. ISBN 978-0-470-04295-3. LCCN 2006041609. OCLC 64085024
- ↑ «Earliest Uses of Some Words of Mathematics». Escócia. Universidade de St. Andrews. Consultado em 3 de fevereiro de 2024 [ligação inativa]
- ↑ Silver, Daniel S. (dezembro de 2017). «The New Language of Mathematics». Sigma Xi. The American Scientist. 105 (6): 364–371. ISSN 0003-0996. LCCN 43020253. OCLC 1480717. doi:10.1511/2017.105.6.364

- ↑ Bellomo, Nicola; Preziosi, Luigi (22 de dezembro de 1994). Modelling Mathematical Methods and Scientific Computation. Col: Mathematical Modeling. 1. [S.l.]: CRC Press. ISBN 978-0-8493-8331-1. Consultado em 16 de novembro de 2022
- ↑ Hennig, Christian (2010). «Mathematical Models and Reality: A Constructivist Perspective». Foundations of Science. 15: 29–48. doi:10.1007/s10699-009-9167-x. Consultado em 17 de novembro de 2022
- ↑ Frigg, Roman; Hartmann, Stephan (4 de fevereiro de 2020). «Models in Science». Stanford Encyclopedia of Philosophy. Consultado em 17 de novembro de 2022. Cópia arquivada em 17 de novembro de 2022
- ↑ Stewart, Ian (2018). «Mathematics, Maps, and Models». In: Wuppuluri; Doria. The Map and the Territory: Exploring the Foundations of Science, Thought and Reality. Col: The Frontiers Collection. [S.l.]: Springer. pp. 345–356. ISBN 978-3-319-72478-2. doi:10.1007/978-3-319-72478-2_18
- ↑ «The science checklist applied: Mathematics». Understanding Science. Universidade da Califórnia em Berkeley. Consultado em 27 de outubro de 2019. Arquivado do original em 27 de outubro de 2019
- ↑ Mackay, A. L. (1991). Dictionary of Scientific Quotations. Londres: Taylor & Francis. ISBN 978-0-7503-0106-0. Consultado em 19 de março de 2023
- ↑ Bishop, Alan (1991). «Environmental activities and mathematical culture». Mathematical Enculturation: A Cultural Perspective on Mathematics Education. Norwell, Massachusetts: Kluwer Academic Publishers. pp. 20–59. ISBN 978-0-7923-1270-3
- ↑ Shasha, Dennis Elliot; Lazere, Cathy A. (1998). Out of Their Minds: The Lives and Discoveries of 15 Great Computer Scientists. [S.l.]: Springer. ISBN 978-0-387-98269-4
- ↑ Nickles, Thomas (2013). «The Problem of Demarcation». Philosophy of Pseudoscience: Reconsidering the Demarcation Problem. Chicago: The University of Chicago Press. ISBN 978-0-226-05182-6
- ↑ Pigliucci, Massimo (2014). «Are There 'Other' Ways of Knowing?». Philosophy Now. Consultado em 6 de abril de 2020. Arquivado do original em 13 de maio de 2020
- ↑ a b Ferreirós, J. (2007). «Ό Θεὸς Άριθμητίζει: The Rise of Pure Mathematics as Arithmetic with Gauss». In: Catherine Goldstein. The Shaping of Arithmetic after C.F. Gauss's Disquisitiones Arithmeticae. [S.l.]: Springer Science & Business Media. pp. 235–268. ISBN 978-3-540-34720-0
- ↑ Kuhn, Thomas S. (1976). «Mathematical vs. Experimental Traditions in the Development of Physical Science». The MIT Press. The Journal of Interdisciplinary History. 7 (1): 1–31. JSTOR 202372. doi:10.2307/202372
- ↑ Asper, Markus (2009). «The two cultures of mathematics in ancient Greece». In: Robson; Stedall. The Oxford Handbook of the History of Mathematics. Col: Oxford Handbooks in Mathematics. [S.l.]: OUP Oxford. pp. 107–132. ISBN 978-0-19-921312-2
- ↑ Gozwami, Pinkimani; Singh, Madan Mohan (2019). «Integer Factorization Problem». In: Ahmad; Doja, M. N.; Udzir, Nur Izura; Singh, Manu Pratap. Emerging Security Algorithms and Techniques. [S.l.]: CRC Press. pp. 59–60. ISBN 978-0-8153-6145-9. LCCN 2019010556. OCLC 1082226900
- ↑ Maddy, P. (2008). «How applied mathematics became pure» (PDF). The Review of Symbolic Logic. 1 (1): 16–41. doi:10.1017/S1755020308080027. Consultado em 19 de novembro de 2022. Cópia arquivada (PDF) em 12 de agosto de 2017
- ↑ Silver, Daniel S. (2017). «In Defense of Pure Mathematics». In: Pitici. The Best Writing on Mathematics, 2016. [S.l.]: Princeton University Press. pp. 17–26. ISBN 978-0-691-17529-4
- ↑ Parshall, Karen Hunger (2022). «The American Mathematical Society and Applied Mathematics from the 1920s to the 1950s: A Revisionist Account». Bulletin of the American Mathematical Society. 59 (3): 405–427. doi:10.1090/bull/1754
 . Consultado em 20 de novembro de 2022. Cópia arquivada em 20 de novembro de 2022
. Consultado em 20 de novembro de 2022. Cópia arquivada em 20 de novembro de 2022
- ↑ Stolz, Michael (2002). «The History Of Applied Mathematics And The History Of Society». Synthese. 133: 43–57. doi:10.1023/A:1020823608217. Consultado em 20 de novembro de 2022
- ↑ Lin, C. C . (Março de 1976). «On the role of applied mathematics». Advances in Mathematics. 19 (3): 267–288. doi:10.1016/0001-8708(76)90024-4

- ↑ Peressini, Anthony (Setembro de 1999). Applying Pure Mathematics (PDF). Philosophy of Science. Proceedings of the 1998 Biennial Meetings of the Philosophy of Science Association. Part I: Contributed Papers. 66. pp. S1–S13. JSTOR 188757. Consultado em 30 de novembro de 2022. Cópia arquivada (PDF) em 2 de janeiro de 2024
- ↑ Lützen, J. (2011). Mathematics meets physics: A contribution to their interaction in the 19th and the first half of the 20th century. Verlag Harri Deutsch. Consultado em 19 de novembro de 2022. Cópia arquivada em 23 de março de 2023
- ↑ Marker, Dave (Julho de 1996). «Model theory and exponentiation». Notices of the American Mathematical Society. 43 (7): 753–759. Consultado em 19 de novembro de 2022. Cópia arquivada em 13 de março de 2014
- ↑ Chen, Changbo; Maza, Marc Moreno (agosto de 2014). Cylindrical Algebraic Decomposition in the RegularChains Library. International Congress on Mathematical Software 2014. Lecture Notes in Computer Science. 8592. Springer. doi:10.1007/978-3-662-44199-2_65. Consultado em 19 de novembro de 2022
- ↑ Pérez-Escobar, José Antonio; Sarikaya, Deniz (2021). «Purifying applied mathematics and applying pure mathematics: how a late Wittgensteinian perspective sheds light onto the dichotomy». European Journal for Philosophy of Science. 12 (1): 1–22. doi:10.1007/s13194-021-00435-9

- ↑ Takase, M. (2014). «Pure Mathematics and Applied Mathematics are Inseparably Intertwined: Observation of the Early Analysis of the Infinity». A Mathematical Approach to Research Problems of Science and Technology. Col: Mathematics for Industry. 5. Tokyo: Springer. pp. 393–399. ISBN 978-4-431-55059-4. doi:10.1007/978-4-431-55060-0_29
- ↑ Sarukkai, Sundar (10 de fevereiro de 2005). «Revisiting the 'unreasonable effectiveness' of mathematics». Current Science. 88 (3): 415–423. JSTOR 24110208
- ↑ Wagstaff, Jr., Samuel S. (2021). «History of Integer Factoring». In: Bos; Stam. Computational Cryptography, Algorithmic Aspects of Cryptography, A Tribute to AKL (PDF). Col: London Mathematical Society Lecture Notes Series 469. [S.l.]: Cambridge University Press. pp. 41–77. Consultado em 20 de novembro de 2022. Cópia arquivada (PDF) em 20 de novembro de 2022
- ↑ «Curves: Ellipse». Universidade de St Andrews. Consultado em 20 de novembro de 2022. Arquivado do original em 14 de outubro de 2022
- ↑ Mukunth, Vasudevan (10 de setembro de 2015). «Beyond the Surface of Einstein's Relativity Lay a Chimerical Geometry». The Wire. Consultado em 20 de novembro de 2022. Arquivado do original em 20 de novembro de 2022
- ↑ Wilson, Edwin B.; Lewis, Gilbert N. (Novembro de 1912). «The Space-Time Manifold of Relativity. The Non-Euclidean Geometry of Mechanics and Electromagnetics». Proceedings of the American Academy of Arts and Sciences. 48 (11): 389–507. JSTOR 20022840. doi:10.2307/20022840
- ↑ a b c Borel, Armand (1983). «Mathematics: Art and Science». Springer. The Mathematical Intelligencer. 5 (4): 9–17. ISSN 1027-488X. doi:10.4171/news/103/8

- ↑ Hanson, Norwood Russell (novembro de 1961). «Discovering the Positron (I)». The University of Chicago Press. The British Journal for the Philosophy of Science. 12 (47): 194–214. JSTOR 685207. doi:10.1093/bjps/xiii.49.54
- ↑ Ginammi, Michele (Fevereiro de 2016). «Avoiding reification: Heuristic effectiveness of mathematics and the prediction of the Ω– particle». Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 53: 20–27. Bibcode:2016SHPMP..53...20G. doi:10.1016/j.shpsb.2015.12.001
- ↑ Wagh, Sanjay Moreshwar; Deshpande, Dilip Abasaheb (27 de setembro de 2012). Essentials of Physics (em inglês). [S.l.]: PHI Learning Pvt. Ltd. ISBN 978-81-203-4642-0. Consultado em 3 de janeiro de 2023
- ↑ Atiyah, Michael (1990). On the Work of Edward Witten (PDF). Proceedings of the International Congress of Mathematicians. p. 31. Consultado em 29 de dezembro de 2022. Cópia arquivada (PDF) em 28 de setembro de 2013
- ↑ Borwein, J.; Borwein, P.; Girgensohn, R.; Parnes, S. (1996). «Conclusion». oldweb.cecm.sfu.ca. Arquivado do original em 21 de janeiro de 2008
- ↑ Hales, Thomas; Adams, Mark; Bauer, Gertrud; Dang, Tat Dat; Harrison, John; Hoang, Le Truong; Kaliszyk, Cezary; Magron, Victor; Mclaughlin, Sean (2017). «A Formal Proof of the Kepler Conjecture». Forum of Mathematics, Pi (em inglês). 5: e2. ISSN 2050-5086. doi:10.1017/fmp.2017.1. Consultado em 25 de fevereiro de 2023. Cópia arquivada em 4 de dezembro de 2020
- ↑ «P versus NP problem | mathematics». Britannica (em inglês). Consultado em 29 de dezembro de 2022. Arquivado do original em 6 de dezembro de 2022
- ↑ a b c Millstein, Roberta (8 de setembro de 2016). «Probability in Biology: The Case of Fitness». In: Hájek, Alan; Hitchcock, Christopher. The Oxford Handbook of Probability and Philosophy (PDF). [S.l.: s.n.] pp. 601–622. doi:10.1093/oxfordhb/9780199607617.013.27. Consultado em 29 de dezembro de 2022. Cópia arquivada (PDF) em 7 de março de 2023
- ↑ See for example Anne Laurent, Roland Gamet, Jérôme Pantel, Tendances nouvelles en modélisation pour l'environnement, actes du congrès «Programme environnement, vie et sociétés» 15-17 janvier 1996, CNRS
- ↑ Bouleau 1999, pp. 282–283.
- ↑ Bouleau 1999, p. 285.
- ↑ «1.4: The Lotka-Volterra Predator-Prey Model». Mathematics LibreTexts (em inglês). 5 de janeiro de 2022. Consultado em 29 de dezembro de 2022. Arquivado do original em 29 de dezembro de 2022
- ↑ Bouleau 1999, p. 287.
- ↑ Edling, Christofer R. (2002). «Mathematics in Sociology». Annual Review of Sociology (em inglês). 28 (1): 197–220. ISSN 0360-0572. doi:10.1146/annurev.soc.28.110601.140942
- ↑ Batchelder, William H. (1 de janeiro de 2015), Wright, James D., ed., Mathematical Psychology: History, ISBN 978-0-08-097087-5, Oxford: Elsevier, pp. 808–815, consultado em 30 de setembro de 2023
- ↑ a b Zak, Paul J. (2010). Moral Markets: The Critical Role of Values in the Economy (em inglês). [S.l.]: Princeton University Press. ISBN 978-1-4008-3736-6. Consultado em 3 de janeiro de 2023
- ↑ a b c Kim, Oliver W. (29 de maio de 2014). «Meet Homo Economicus». The Harvard Crimson. Consultado em 29 de dezembro de 2022. Arquivado do original em 29 de dezembro de 2022
- ↑ «Kondratiev, Nikolai Dmitrievich | Encyclopedia.com». www.encyclopedia.com. Consultado em 29 de dezembro de 2022. Arquivado do original em 1 de julho de 2016
- ↑ «Mathématique de l'histoire-géometrie et cinématique. Lois de Brück. Chronologie géodésique de la Bible., by Charles LAGRANGE et al. | The Online Books Page». onlinebooks.library.upenn.edu
- ↑ «Cliodynamics: a science for predicting the future». ZDNET (em inglês). Consultado em 29 de dezembro de 2022. Arquivado do original em 29 de dezembro de 2022
- ↑ Sokal, Alan; Jean Bricmont (1998). Fashionable Nonsense. New York: Picador. ISBN 978-0-312-19545-8. OCLC 39605994
- ↑ Beaujouan, Guy (1994). Comprendre et maîtriser la nature au Moyen Age: mélanges d'histoire des sciences offerts à Guy Beaujouan (em francês). [S.l.]: Librairie Droz. ISBN 978-2-600-00040-6. Consultado em 3 de janeiro de 2023
- ↑ «L'astrologie à l'épreuve : ça ne marche pas, ça n'a jamais marché ! / Afis Science – Association française pour l'information scientifique». Afis Science – Association française pour l’information scientifique (em francês). Consultado em 28 de dezembro de 2022. Arquivado do original em 29 de janeiro de 2023
- ↑ Dorato, Mauro (2005). «Why are laws mathematical?». The Software of the Universe, An Introduction to the History and Philosophy of Laws of Nature (PDF). [S.l.]: Ashgate. pp. 31–66. ISBN 978-0-7546-3994-7. Consultado em 5 de dezembro de 2022. Cópia arquivada (PDF) em 17 de agosto de 2023
- ↑ a b c Mura, Roberta (Dezembro de 1993). «Images of Mathematics Held by University Teachers of Mathematical Sciences». Educational Studies in Mathematics. 25 (4): 375–85. JSTOR 3482762. doi:10.1007/BF01273907
- ↑ a b Tobies, Renate; Neunzert, Helmut (2012). Iris Runge: A Life at the Crossroads of Mathematics, Science, and Industry. [S.l.]: Springer. ISBN 978-3-0348-0229-1. Consultado em 20 de junho de 2015
- ↑ Ziegler, Günter M.; Loos, Andreas (2 de novembro de 2017). "What is Mathematics?" and why we should ask, where one should experience and learn that, and how to teach it. Proceedings of the 13th International Congress on Mathematical Education. ICME-13 Monographs. Springer. pp. 63–77. ISBN 978-3-319-62596-6. doi:10.1007/978-3-319-62597-3_5
- ↑ Franklin, James (2009). Philosophy of Mathematics. [S.l.]: Elsevier. pp. 104–106. ISBN 978-0-08-093058-9. Consultado em 20 de junho de 2015
- ↑ Cajori, Florian (1893). A History of Mathematics. [S.l.]: American Mathematical Society (1991 reprint). pp. 285–286. ISBN 978-0-8218-2102-2. Consultado em 20 de junho de 2015
- ↑ Brown, Ronald; Porter, Timothy (Janeiro de 2000). «The Methodology of Mathematics». The Mathematical Gazette. 79 (485): 321–334. JSTOR 3618304. doi:10.2307/3618304. Consultado em 25 de novembro de 2022. Cópia arquivada em 23 de março de 2023
- ↑ Strauss, Danie (2011). «Defining mathematics». Acta Academica. 43 (4): 1–28. Consultado em 25 de novembro de 2022
- ↑ Hamami, Yacin (Junho de 2022). «Mathematical Rigor and Proof» (PDF). The Review of Symbolic Logic. 15 (2): 409–449. doi:10.1017/S1755020319000443. Consultado em 21 de novembro de 2022. Cópia arquivada (PDF) em 5 de dezembro de 2022
- ↑ Peterson 1988, p. 4: "A few complain that the computer program can't be verified properly." (in reference to the Haken–Apple proof of the Four Color Theorem)
- ↑ Perminov, V. Ya. (1988). «On the Reliability of Mathematical Proofs». Revue Internationale de Philosophie. Philosophy of Mathematics. 42 (167 (4)): 500–508
- ↑ Davis, Jon D.; McDuffie, Amy Roth; Drake, Corey; Seiwell, Amanda L. (2019). «Teachers' perceptions of the official curriculum: Problem solving and rigor». International Journal of Educational Research. 93: 91–100. doi:10.1016/j.ijer.2018.10.002
- ↑ Endsley, Kezia (2021). Mathematicians and Statisticians: A Practical Career Guide. Col: Practical Career Guides. [S.l.]: Rowman & Littlefield. pp. 1–3. ISBN 978-1-5381-4517-3. Consultado em 29 de novembro de 2022
- ↑ Robson, Eleanor (2009). «Mathematics education in an Old Babylonian scribal school». In: Robson; Stedall. The Oxford Handbook of the History of Mathematics. [S.l.]: OUP Oxford. ISBN 978-0-19-921312-2
- ↑ Bernard, Alain; Proust, Christine; Ross, Micah (2014). «Mathematics Education in Antiquity». In: Karp; Schubring. Handbook on the History of Mathematics Education. Nova York: Springer. pp. 27–53. ISBN 978-1-4614-9154-5. doi:10.1007/978-1-4614-9155-2_3
- ↑ Dudley, Underwood (Abril de 2002). «The World's First Mathematics Textbook». Taylor & Francis, Ltd. Math Horizons. 9 (4): 8–11. JSTOR 25678363. doi:10.1080/10724117.2002.11975154
- ↑ Subramarian, F. Indian pedagogy and problem solving in ancient Thamizhakam (PDF). History and Pedagogy of Mathematics conference, July 16–20, 2012. Consultado em 29 de novembro de 2022. Cópia arquivada (PDF) em 28 de novembro de 2022
- ↑ Siu, Man Keung (2004). «Official Curriculum in Mathematics in Ancient China: How did Candidates Study for the Examination?». How Chinese Learn Mathematics (PDF). Col: Series on Mathematics Education. 1. [S.l.: s.n.] pp. 157–185. ISBN 978-981-256-014-8. doi:10.1142/9789812562241_0006. Consultado em 26 de novembro de 2022
- ↑ Jones, Phillip S. (1967). «The History of Mathematical Education». Taylor & Francis, Ltd. The American Mathematical Monthly. 74 (1): 38–55. JSTOR 2314867. doi:10.2307/2314867
- ↑ Schubring, Gert; Furinghetti, Fulvia; Siu, Man Keung (Agosto de 2012). «Introduction: the history of mathematics teaching. Indicators for modernization processes in societies». ZDM Mathematics Education. 44 (4): 457–459. doi:10.1007/s11858-012-0445-7

- ↑ von Davier, Matthias; Foy, Pierre; Martin, Michael O.; Mullis, Ina V.S. (2020). «Examining eTIMSS Country Differences Between eTIMSS Data and Bridge Data: A Look at Country-Level Mode of Administration Effects». TIMSS 2019 International Results in Mathematics and Science (PDF) (em inglês). [S.l.]: TIMSS & PIRLS International Study Center, Lynch School of Education and Human Development and International Association for the Evaluation of Educational Achievement. ISBN 978-1-889938-54-7. Consultado em 29 de novembro de 2022. Cópia arquivada (PDF) em 29 de novembro de 2022
- ↑ Rowan-Kenyon, Heather T.; Swan, Amy K.; Creager, Marie F. (Março de 2012). «Social Cognitive Factors, Support, and Engagement: Early Adolescents' Math Interests as Precursors to Choice of Career» (PDF). The Career Development Quarterly. 60 (1): 2–15. doi:10.1002/j.2161-0045.2012.00001.x. Consultado em 29 de novembro de 2022. Cópia arquivada (PDF) em 22 de novembro de 2023
- ↑ Luttenberger, Silke; Wimmer, Sigrid; Paechter, Manuela (2018). «Spotlight on math anxiety». Psychology Research and Behavior Management. 11: 311–322. PMC 6087017
 . PMID 30123014. doi:10.2147/PRBM.S141421
. PMID 30123014. doi:10.2147/PRBM.S141421
- ↑ Yaftian, Narges (2 de junho de 2015). «The Outlook of the Mathematicians' Creative Processes». Procedia - Social and Behavioral Sciences. 191: 2519–2525. doi:10.1016/j.sbspro.2015.04.617

- ↑ Nadjafikhah, Mehdi; Yaftian, Narges (10 de outubro de 2013). «The Frontage of Creativity and Mathematical Creativity». Procedia - Social and Behavioral Sciences. 90: 344–350. doi:10.1016/j.sbspro.2013.07.101

- ↑ van der Poorten, A. (1979). «A proof that Euler missed... Apéry's Proof of the irrationality of ζ(3)» (PDF). The Mathematical Intelligencer. 1 (4): 195–203. doi:10.1007/BF03028234. Consultado em 22 de novembro de 2022. Cópia arquivada (PDF) em 6 de setembro de 2015
- ↑ Petkovi, Miodrag (2 de setembro de 2009). Famous Puzzles of Great Mathematicians. [S.l.]: American Mathematical Society. pp. xiii–xiv. ISBN 978-0-8218-4814-2. Consultado em 25 de novembro de 2022
- ↑ Hardy, G. H. (1940). A Mathematician's Apology. [S.l.]: Cambridge University Press. ISBN 978-0-521-42706-7. Consultado em 22 de novembro de 2022 See also A Mathematician's Apology.
- ↑ Alon, Noga; Goldston, Dan; Sárközy, András; Szabados, József; Tenenbaum, Gérald; Garcia, Stephan Ramon; Shoemaker, Amy L. (Março de 2015). Krishnaswami, Alladi; Krantz, Steven G., eds. «Reflections on Paul Erdős on His Birth Centenary, Part II». Notices of the American Mathematical Society. 62 (3): 226–247. doi:10.1090/noti1223

- ↑ See, for example Bertrand Russell's statement "Mathematics, rightly viewed, possesses not only truth, but supreme beauty ..." in his History of Western Philosophy. [S.l.: s.n.] 1919
- ↑ Cazden, Norman (outubro de 1959). «Musical intervals and simple number ratios». Journal of Research in Music Education. 7 (2): 197–220. JSTOR 3344215. doi:10.1177/002242945900700205
- ↑ Budden, F. J. (Outubro de 1967). «Modern mathematics and music». Cambridge University Press ({CUP}). The Mathematical Gazette. 51 (377): 204–215. JSTOR 3613237. doi:10.2307/3613237
- ↑ Enquist, Magnus; Arak, Anthony (Novembro de 1994). «Symmetry, beauty and evolution». Nature (em inglês). 372 (6502): 169–172. Bibcode:1994Natur.372..169E. ISSN 1476-4687. PMID 7969448. doi:10.1038/372169a0. Consultado em 29 de dezembro de 2022. Cópia arquivada em 28 de dezembro de 2022
- ↑ Hestenes, David (1999). «Symmetry Groups» (PDF). geocalc.clas.asu.edu. Consultado em 29 de dezembro de 2022. Arquivado do original (PDF) em 1 de janeiro de 2023
- ↑ Bender, Sara (Setembro de 2020). «The Rorschach Test». In: Carducci; Nave, Christopher S.; Mio; Riggio, Ronald E. The Wiley Encyclopedia of Personality and Individual Differences: Measurement and Assessment. Wiley. pp. 367–376. ISBN 978-1-119-05751-2. doi:10.1002/9781119547167.ch131
- ↑ Weyl, Hermann (2015). Symmetry. Col: Princeton Science Library. 47. [S.l.]: Princeton University Press. ISBN 978-1-4008-7434-7
- ↑ Bradley, Larry (2010). «Fractals – Chaos & Fractals». www.stsci.edu. Consultado em 29 de dezembro de 2022. Arquivado do original em 7 de março de 2023
- ↑ «Self-similarity». math.bu.edu. Consultado em 29 de dezembro de 2022. Arquivado do original em 2 de março de 2023
- ↑ Kissane, Barry (Julho de 2009). Popular mathematics. 22nd Biennial Conference of The Australian Association of Mathematics Teachers. Fremantle, Western Australia: Australian Association of Mathematics Teachers. pp. 125–126. Consultado em 29 de dezembro de 2022. Cópia arquivada em 7 de março de 2023
- ↑ Steen, L. A. (2012). Mathematics Today Twelve Informal Essays (em inglês). [S.l.]: Springer Science & Business Media. ISBN 978-1-4613-9435-8. Consultado em 3 de janeiro de 2023
- ↑ Pitici, Mircea (2017). The Best Writing on Mathematics 2016 (em inglês). [S.l.]: Princeton University Press. ISBN 978-1-4008-8560-2. Consultado em 3 de janeiro de 2023
- ↑ Monastyrsky 2001, p. 1: "The Fields Medal is now indisputably the best known and most influential award in mathematics."
- ↑ Riehm 2002, pp. 778–782.
- ↑ «Fields Medal | International Mathematical Union (IMU)». www.mathunion.org. Consultado em 21 de fevereiro de 2022. Arquivado do original em 26 de dezembro de 2018
- ↑ a b «Fields Medal». Maths History (em inglês). Consultado em 21 de fevereiro de 2022. Arquivado do original em 22 de março de 2019
- ↑ Universidade de St. Andrews (ed.). «Honours/Prizes Index». Consultado em 20 de fevereiro de 2023. Arquivado do original em 17 de dezembro de 2021
- ↑ «About the Abel Prize». The Abel Prize. Consultado em 23 de janeiro de 2022. Arquivado do original em 14 de abril de 2022
- ↑ «Abel Prize | mathematics award». Encyclopedia Britannica (em inglês). Consultado em 23 de janeiro de 2022. Arquivado do original em 26 de janeiro de 2020
- ↑ «Chern Medal Award» (PDF). www.mathunion.org. 1 de junho de 2009. Consultado em 21 de fevereiro de 2022. Arquivado do original (PDF) em 17 de junho de 2009
- ↑ «Chern Medal Award». International Mathematical Union (IMU). Consultado em 23 de janeiro de 2022. Arquivado do original em 25 de agosto de 2010
- ↑ «The Leroy P Steele Prize of the AMS». School of Mathematics and Statistics, University of St Andrews, Scotland. Consultado em 17 de novembro de 2022. Arquivado do original em 17 de novembro de 2022
- ↑ Chern, S. S.; Hirzebruch, F. (Setembro de 2000). Wolf Prize in Mathematics (em inglês). [S.l.: s.n.] ISBN 978-981-02-3945-9. doi:10.1142/4149. Consultado em 21 de fevereiro de 2022. Cópia arquivada em 21 de fevereiro de 2022
- ↑ «The Wolf Prize». Wolf Foundation (em inglês). Consultado em 23 de janeiro de 2022. Arquivado do original em 12 de janeiro de 2020
- ↑ a b «Hilbert's Problems: 23 and Math». Simons Foundation (em inglês). 6 de maio de 2020. Consultado em 23 de janeiro de 2022. Arquivado do original em 23 de janeiro de 2022
- ↑ Feferman, Solomon (1998). «Deciding the undecidable: Wrestling with Hilbert's problems». In the Light of Logic. Col: Logic and Computation in Philosophy series. [S.l.]: Oxford University Press. pp. 3–27. ISBN 978-0-19-508030-8. Consultado em 29 de novembro de 2022
- ↑ «The Millennium Prize Problems». Clay Mathematics Institute. Consultado em 23 de janeiro de 2022. Arquivado do original em 3 de julho de 2015
- ↑ «Millennium Problems». Clay Mathematics Institute. Consultado em 23 de janeiro de 2022. Arquivado do original em 20 de dezembro de 2018
Bibliografia
- Bouleau, Nicolas (1999). Philosophie des mathématiques et de la modélisation: Du chercheur à l'ingénieur. [S.l.]: L'Harmattan. ISBN 978-2-7384-8125-2
- Boyer, Carl Benjamin (1991). A History of Mathematics 2ª ed. Nova York: Wiley. ISBN 978-0-471-54397-8
- Eves, Howard (1990). An Introduction to the History of Mathematics 6th ed. [S.l.]: Saunders. ISBN 978-0-03-029558-4
- Kleiner, Israel (2007). Kleiner, Israel, ed. A History of Abstract Algebra. [S.l.]: Springer Science & Business Media. ISBN 978-0-8176-4684-4. LCCN 2007932362. OCLC 76935733. doi:10.1007/978-0-8176-4685-1. Consultado em 8 de fevereiro de 2024
- Kline, Morris (1990). Mathematical Thought from Ancient to Modern Times. Nova York: Oxford University Press. ISBN 978-0-19-506135-2
- Monastyrsky, Michael (2001). «Some Trends in Modern Mathematics and the Fields Medal» (PDF). Canadian Mathematical Society. CMS – Notes – de la SMC. 33 (2–3). Consultado em 28 de julho de 2006. Arquivado do original (PDF) em 13 de agosto de 2006
- Oakley, Barbara (2014). A Mind For Numbers: How to Excel at Math and Science (Even If You Flunked Algebra). Nova York: Penguin Random House. ISBN 978-0-399-16524-5.
A Mind for Numbers.
- Peirce, Benjamin (1881). Peirce, Charles Sanders, ed. «Linear associative algebra» Corrected, expanded, and annotated revision with an 1875 paper by B. Peirce and annotations by his son, C.S. Peirce, of the 1872 lithograph ed. American Journal of Mathematics. 4 (1–4): 97–229. JSTOR 2369153. doi:10.2307/2369153. hdl:2027/hvd.32044030622997
 . Corrected, expanded, and annotated revision with an 1875 paper by B. Peirce and annotations by his son, C. S. Peirce, of the 1872 lithograph ed. Google Eprint and as an extract, D. Van Nostrand, 1882, Google Eprint. Consultado em 17 de novembro de 2020.
. Corrected, expanded, and annotated revision with an 1875 paper by B. Peirce and annotations by his son, C. S. Peirce, of the 1872 lithograph ed. Google Eprint and as an extract, D. Van Nostrand, 1882, Google Eprint. Consultado em 17 de novembro de 2020. - Peterson, Ivars (1988). The Mathematical Tourist: Snapshots of Modern Mathematics. [S.l.]: W. H. Freeman and Company. ISBN 0-7167-1953-3. LCCN 87033078. OCLC 17202382
- Popper, Karl R. (1995). «On knowledge». In Search of a Better World: Lectures and Essays from Thirty Years. New York: Routledge. Bibcode:1992sbwl.book.....P. ISBN 978-0-415-13548-1
- Riehm, Carl (Agosto de 2002). «The Early History of the Fields Medal» (PDF). Notices of the AMS. 49 (7): 778–782. Consultado em 2 de outubro de 2006. Arquivado do original (PDF) em 26 de outubro de 2006
- Sevryuk, Mikhail B. (Janeiro de 2006). «Book Reviews» (PDF). Bulletin of the American Mathematical Society. 43 (1): 101–109. doi:10.1090/S0273-0979-05-01069-4. Consultado em 24 de junho de 2006. Arquivado do original (PDF) em 23 de julho de 2006
- Whittle, Peter (1994). «Almost home». In: Kelly, F.P. Probability, statistics and optimisation: A Tribute to Peter Whittle previously "A realised path: The Cambridge Statistical Laboratory up to 1993 (revised 2002)" ed. Chichester: John Wiley. pp. 1–28. ISBN 978-0-471-94829-2. Arquivado do original em 19 de dezembro de 2013


